Static equilibrium
All parts of the system are at rest. Ftotal = τtotal = 0
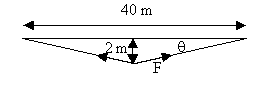
2Fy = mg, Fy = 9.8*0.25 N = 2.45 N.
sinθ = 2/(4 + 400)½.
F = Fy/sinθ = 24.6 N is the tension in the wire.
Static equilibrium
Two telephone poles are separated by 40 m and connected by a massless wire. A bird of mass 0.5 kg lands on the wire midway between the poles, causing the wire to sag 2.0 m below horizontal. What is the tension in the wire?
Solution:

One end of a spring of negligible mass is attached to the ceiling. When a 250 g mass is placed on the free end (without stretching the spring) and then released, the mass descends 20.0 cm before it changes direction and begins to ascend. What is the spring constant k (in N/m)?
Solution:
Two
identical springs with spring constant k = 1 N/m and equilibrium length l
= 0.25 m are connected by a middle string of length L = (3/8) m and support a
weight w = 0.5 N.
Two strings of length 1 m are loosely connected as shown.
Find the position of the weight below the support and show that it moves up when
the middle string is cut.
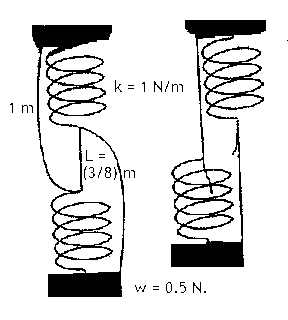
Solution:
Consider a particle moving along the x axis under the influence of the potential
U(x) = ½k(x/a)2 - (1/3)k(x/a)3
where k and a are constants.
(a) Plot the potential.
(b) Find the equilibrium point(s).
(c) Determine whether the equilibrium point(s) are stable or unstable.
Solution:
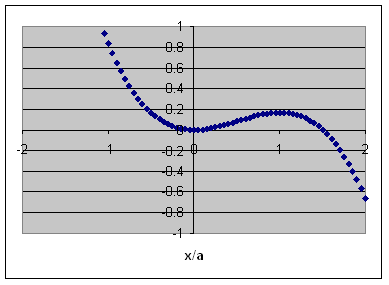
(b) Let x' = x/a.
F = -dU/dx' = -kx' + kx'2 = 0. x' = x'2, x/a = 0,
1 are the equilibrium points.
(c) dF/dx' = -k + 2kx'.
dF/dx'|x'= 0 = -k --> stable equilibrium (restoring force).
dF/dx'|x'= 1 = k --> unstable equilibrium.
Two small positively charged spheres are suspended from a common point at the ceiling by the insulating light strings of equal length. The first sphere has mass m1 and charge q1 while the second one has mass m2 and charge q2. If the first string makes an angle θ1 with the vertical, find the angle θ2 that the second string makes with the vertical.
Solution: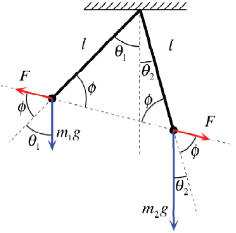
Dynamic equilibrium
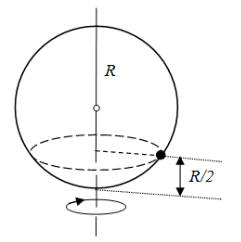
A hollow sphere of radius R = 0.5 m rotates about a vertical axis
through its center with an angular velocity of ω = 5/s. Inside the
sphere a small block is moving together with the sphere at the height of R/2.
(Let g = 10 m/s2.)
(a) What is the minimal coefficient of friction to fulfill this
condition?
(b) Find the minimal coefficient of friction for the case of ω =
8/s.
(c) Given the minimal coefficient of friction, investigate the
problem of stability in both cases,
(i) for a small change of the position of the block,
(ii) for a small change of the angular velocity of the sphere.
Solution:
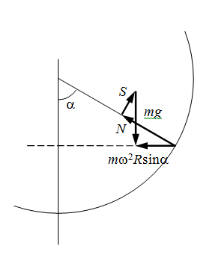
(a) For the horizontal and
vertical components we of Fnet we have
mω2R sinα = N sinα -
S cosα, mg = N cosα + S sinα.
Solving for S and N we
obtain
S = mg sinα [1 - ω2 R cosα/g],
N = mg [cosα
+ ω2 R sin2α/g]
The block
does not slip down if μα = ≥
|S/N| = sinα |1 - ω2 R cosα/g]|/[cosα
+
ω2 R sin2α/g].
If ω2 R cosα/g < 1 then S
points upward, the frictional force prevents the block from sliding
down. This is the case for ω = 5/s. We have α = 60o and
μα min = 0.2259.
(b) If ω2 R cosα/g >1 then S
points downward, the frictional force prevents the block from sliding
up. This is the case for ω = 8/s, and μαmin = 0.1792.
(c) In case (a) the direction of the frictional force prevents
the block from sliding down.
μα min increases when α increases by a small amount
and decreases when α decreases by a small amount. If the block is
displaced upwards, it slips downward,
if it is displaced downward, it stays. If ω increases be
a small amount, the block remains
in equilibrium, if ω decreases by a small amount, it slips downwards.
In case (b) the direction of the frictional force prevents the block
from sliding up.
μα min increases when α decreases by a small amount
and decreases when α increases by a small amount. If the block is
displaced upwards, it stays,
if it is displaced downward, it slips upward. If ω
decreases by a small amount, the block remains
in equilibrium, if ω increases by a small amount, it slips upward.