Motion in a non-inertial frame

Linear acceleration

Problem:

At t = 0 a 100 g ball is thrown upward with initial speed v = 2 m/s in an open-platform elevator which at that time is moving downward with v = 3 m/s and accelerating downward with an acceleration of magnitude a = 3 m/s².  A drag force with magnitude F_drag = 0.8 N acts on the ball. 
(a)  What is the net force F_net acting on the ball in the frame of the elevator just after it has been thrown?
(b)  What is the net force F_net acting on the ball in the frame of a person standing on the ground just after it has been thrown?

Solution:

• Concepts:
  Motion in an accelerating frame
• Reasoning:
  Fictitious forces appear in an accelerating frame.
  In the inertial frame the ball moves downward just after it is thrown, the drag force which opposes the relative motion of the ball and the air therefore points upward.
• Details of the calculation:
  Let the upward direction be the positive y -direction.
  (a)  F_net = mg - ma + F_drag = (-mg + ma + F_drag) j = (-0.1*6.8 N + 0.8 N) j
  = 0.12 N j.  The ball accelerates upward in the frame of the elevator.
  (b)  F_net = mg + F_drag = (-mg + Fd_rag) j = (-0.1*9.8 N + 0.8 N) j = 0.18 N j.
  The ball accelerates downward in the frame of the person on the ground.

Problem:

A hauling truck is traveling on a level road. The driver suddenly applies the brakes, causing the truck to decelerate by an amount g/2.  This causes a box in the rear of the truck to slide forward. If the coefficient of sliding friction between the box and the truck bed is (1/3), find the acceleration of the box relative to
(a) the truck and
(b) the road.

Solution:

• Concepts:
  Motion in an accelerating frame.
• Reasoning:
  In an accelerating frame fictitious forces appear.  The net force in such a frame is
  F = F_inertial - ma, where a is the acceleration of the frame.
• Details of the calculation:
  This is a one-dimensional problem.  Let the positive direction be the direction of the trucks initial velocity.
  (a)  F = -mg/3 + mg/2 = +mg/6.  The acceleration of the box relative to the truck is g/6.
  (b)  F = -mg/3.  The acceleration of the box relative to the road is -g/3.

Problem:

(a)  An elevator in which a woman is standing moves upward at 4 m/s.  If the woman drops a coin from a height 1.4 m above the elevator floor, how long does it take the coin to strike the floor?  What is the speed of the coin relative to the floor just before impact? 
(b)  Now assume that the elevator is moving downward with zero initial velocity and acceleration of 1 m/s² at t = 0, the women releases the coin at t = 1 s.  How long does it take the coin to strike the floor?  What is the speed of the coin relative to the floor just before impact?

Solution:

• Concepts:
  The equations of motion in an inertial and in an accelerating frame.
• Reasoning:
  For part (a) the elevator is an inertial frame and for part (b) it is an accelerating frame.
• Details of the calculations:
  (a) The elevator is an inertial frame.  The time it takes the coin to reach the floor is
  t = (2h/g)^½ = 0.53 s.
  The speed just before impact is v = gt = 5.24 m/s.
  (b)  Now the elevator is an accelerating frame.
  In non-inertial frames fictitious forces appear. 
  Consider a particle moving with velocity v in a reference frame K which moves with velocity V(t) relative to the inertial frame K₀.
  The equations of motion are
  mdv/dt = mg - mdV/dt .
  Here dv/dt = g - 1 m/s² = 8.8 m/s² = g', downward.
  t = (2h/g')^½ = 0.56 s.
  The speed just before impact is v = g't = 4.96 m/s.

Problem:

A water tank sits on a horizontal truck bed.

The truck accelerates with uniform acceleration a = 2.5 m/s² in the positive x-direction.   Find the angle α the water's surface makes with the horizontal.

Solution:

• Concepts:
  Non-inertial frames
  
• Reasoning:
  The truck is a non-inertial frame
  In an accelerating frame fictitious forces appear.  The net force in a linearly accelerating frame is
  F = F_inertial - ma, where a is the acceleration of the frame.
• Details of the calculation:
  

  Here F = mg - ma.
  Let the y-axis point upward.  Then F = -m(9.8 m/s² j + 2.5 m/s² i).
  The water's surface is perpendicular to F.
  It slopes upward towards the back of the truck.  The slope dy/dx = -a/g = -0.255 = tan(α).
  α = 165.7^o or -14.3^o.

   

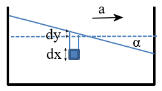
  Or, observe a volume dV = (dx)³ in the accelerating tank from an inertial frame. 
  The pressure in the liquid depends on the depth below the surface.  The pressure on the left side is higher that the pressure on the right side of dV by an amount ρg|dy|.
  The net force on dV is F = ρgdy(dx)².  It accelerates the water in dV.  We have F = ma.
  ρgdy(dx)² = ρ(dx)³a.  |dy|/dx = a/g is the magnitude of the slope.  The slope is negative.

Rotating frames

Problem:

Write F = ma in a rotating coordinate system and identify Coriolis and centrifugal terms.

Solution:

• Concepts:
  Motion in a non-inertial frame
• Reasoning:
  A rotating coordinate system is a non-inertial frame.  Fictitious forces appear.
• Details of the calculation:
  The relationship between the time derivatives of any vector A in a fixed, inertial frame and in a frame rotating with constant angular velocity Ω is
  (dA/dt)_fixed = (dA/dt)_rotating + Ω × A.
  Therefore:
  (dr/dt)_fixed = (dr/dt)_rotating + Ω × r.
  The relationship between the velocity v_i in the inertial frame and the velocity v in a frame rotating with constant angular velocity Ω is
  v_i = v + Ω × r.
  Differentiating again we have
  (dv_i/dt)_fixed = (dv/dt)_fixed + Ω × (dr/dt)_fixed.
  Inserting (dr/dt)_fixed from above we have
  m(dv_i/dt)_fixed = F_i = m(dv/dt)_fixed + mΩ × v + mΩ × (Ω × r).
  Now we use
  (dv/dt)_fixed = (dv/dt)_rotating + Ω × v
  to obtain the equations of motion in the rotating frame.
  The equations of motion in the rotating frame therefore are
  mdv/dt = F_i - 2mΩ × v - mΩ × (Ω × r).
  If F_i is derivable from a potential then F_i = -∂U/∂r.
  2m(v × Ω) = -2m(Ω × v) = Coriolis force
  m(Ω × r) × Ω = -mΩ × (Ω × r) = centrifugal force

Problem:

A disc of radius R is spinning in the horizontal plane with a constant angular speed Ω.  A ladybug walks along the radius of the spinning disc, traveling from the center of the disc toward the edge. The ladybug maintains a constant speed v relative to the disc.
What is the acceleration of the ladybug at the instant it reaches the edge of the disc?

Solution:

• Concepts:
  Motion viewed from an inertial and a non-inertial frame
• Reasoning:
  In non-inertial frames fictitious forces appear.
• Details of the calculation:
  Consider a particle moving with velocity v in a reference frame K which moves with velocity V(t) relative to the inertial frame K₀ and rotates with angular velocity Ω(t).  The equations of motion are in the non-inertial frame are
  mdv/dt = F_inertial - mdV/dt  + mr × dΩ/dt - 2mΩ × v - mΩ × (Ω × r).
  Here
  -mdV/dt = fictitious force due to acceleration of frame,
  mr × dΩ/dt = fictitious force due to non-uniform rotation of frame,
  -2mΩ × v = Coriolis force,
  -mΩ × (Ω × r) = Centifugal force.
  In the inertial frame we have
  F_inertial = mdv/dt + mdV/dt  - mr × dΩ/dt + 2mΩ × v + mΩ × (Ω × r).
  Details of the calculation:
  For the bug dv/dt = dV/dt = dΩ/dt = 0.
  F_inertial = 2mΩ × v + mΩ × (Ω × r).
  In the inertial frame the magnitudes of the tangential and radial force are
  F_tangential =  2mvΩ,  F_rad = mΩ²r.
  In the inertial frame the magnitudes of the tangential and radial acceleration are therefore given by
  a_tangential = 2vΩ,  a_rad = Ω²r
  At the instant the bug reaches the edge of the disk
  a = (a_tangential² + a_rad²)^½ = Ω(4v² + Ω²R ²)^½.

Problem:

An object on a planar platform moves in an elliptical trajectory described by
x(t) = x₁ + x₂ cos(αt),   y(t) = y₁ + y₂ sin(αt),
where x and y are measured with respect to a coordinate system fixed on the platform.  The platform is rotating with respect to an inertial coordinate system XYZ.  The two coordinate systems XYZ and xyz are the same at time t = 0.  The axis of rotation is the Z-axis, but the angular speed of rotation is fluctuating with time and is given by
ω(t) = ω₁ + ω₂ sin(βt).
Find an expression for the velocity components V_x and V_y of the object in the inertial frame at time.

Solution:

• Concepts:
  Rotating coordinate systems, v_fixed = v_rot + ω × r
• Reasoning:
  The position of an object as a function of time is given in a non-inertial (rotating) frame.  We are asked to find the velocity of the object in an inertial frame.
• Details of the calculation:
  Assume the platform is rotating counterclockwise.  Then

  ,    .

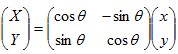  Given :  x(t) = x₁ + x₂ cos(αt),   y(t) = y₁ + y₂ sin(αt) 
  Therefore:  dx/dt = -α x₂ sin(αt),  dy/dt = α y₂ cos(αt)
  Given : ω(t) = ω₁ + ω₂ sin(βt),  θ(t= 0) = 0
  Therefore:  θ(t) = ω₁t + (ω₂/β)(1 - cos(βt))
  V_x = dX/dt = d(cosθ x - sinθ y)/dt
  = cosθ dx/dt - x sinθ dθ/dt - sinθ dy/dt - y cosθ dθ/dt
  = cosθ dx/dt - sinθ dy/dt - (x sinθ  + y cosθ)dθ/dt
  V_y = dY/dt = d(cosθ y + sinθ x)/dt
  = cosθ dy/dt - y sinθ dθ/dt + sinθ dx/dt + x cosθ dθ/dt
  = sinθ dx/dt + cosθ dy/dt + (x cosθ - y sinθ)dθ/dt

  Inserting:
  V_x = -cos(ω₁t + (ω₂/β)(1 - cos(βt)))α x₂ sin(αt) - sin(ω₁t + (ω₂/β)(1 - cos(βt)))α y₂ cos(αt)
  - [(x₁+x₂ cos(αt)) sin(ω₁t + (ω₂/β)(1 - cos(βt))) + (y₁+y₂ sin(αt))(cos(ω₁t + (ω₂/β)(1 - cos(βt)))]
  *( ω₁ + ω₂ sin(βt))

  V_y = -sin(ω₁t + (ω₂/β)(1 - cos(βt)))α x₂ sin(αt) + cos(ω₁t + (ω₂/β)(1 - cos(βt))) α y₂ cos(αt)
  + [(x₁+x₂ cos(αt)) cos(ω₁t + (ω₂/β)(1 - cos(βt))) - (y₁+y₂ sin(αt))(sin(ω₁t + (ω₂/β)(1 - cos(βt)))]
  *( ω₁ + ω₂ sin(βt))
  
  Verify that v_fixed = v_rot + ω × r.
  ω = ωk.  ω × r = -ω(t)y(t)i + ω(t)x(t)j
  v_fixed = (-α x₂ sin(αt) -ω(t)y(t))i + (α y₂ cos(αt) + ω(t)x(t))j
  Here v_fixed is expressed in terms of the coordinates in the rotating system.
  Change to the coordinates of the inertial system:
  V_x = cosθ(-α x₂ sin(αt) -ω(t)y(t)) - sinθ(α y₂ cos(αt) + ω(t)x(t))
  = -cosθ(α x₂ sin(αt)) - sinθ(α y₂ cos(αt)) - [cosθ y(t)) + sinθ x(t)]ω(t)
  = -cos(ω₁t + (ω₂/β)(1 - cos(βt)))α x₂ sin(αt) - sin(ω₁t + (ω₂/β)(1 - cos(βt)))α y₂ cos(αt)
  - [(x₁+x₂ cos(αt)) sin(ω₁t + (ω₂/β)(1 - cos(βt))) + (y₁+y₂ sin(αt))(cos(ω₁t + (ω₂/β)(1 - cos(βt)))]
  *(ω₁ + ω₂ sin(βt))
  Similarly
  V_y = sinθ(-α x₂ sin(αt) -ω(t)y(t)) + cosθ(α y₂ cos(αt) + ω(t)x(t))
  = -sinθ(α x₂ sin(αt)) + cosθ(α y₂ cos(αt)) - [sinθ y(t)) - cosθ x(t)]ω(t)
  = -sin(ω₁t + (ω₂/β)(1 - cos(βt)))α x₂ sin(αt) + cos(ω₁t + (ω₂/β)(1 - cos(βt))) α y₂ cos(αt)
  + [(x₁+x₂ cos(αt)) cos(ω₁t + (ω₂/β)(1 - cos(βt))) - (y₁+y₂ sin(αt))(sin(ω₁t + (ω₂/β)(1 - cos(βt)))]
  *(ω₁ + ω₂ sin(βt))

Problem:

A brave physics student (an undergraduate, of course) climbs aboard a high powered merry-go-round and goes to the center, at r = 0.  At time t = 0, the platform starts from rest (Ω = 0) and begins to spin about its vertical axis with constant angular acceleration α.  Also at time t = 0, the student begins to crawl radially outward at constant speed v, relative to the platform.
Assuming the student does not slip, find the student's acceleration in the inertial frame of an outside observer.

Solution:

• Concepts:
  Motion viewed from an inertial and a non-inertial frame
• Reasoning:
  In non-inertial frames fictitious forces appear. 
  Consider a particle moving with velocity v in a reference frame K which moves with velocity V(t) relative to the inertial frame K₀ and rotates with angular velocity Ω(t). 
  The equations of motion are in the non-inertial frame are
  mdv/dt = F_inertial - mdV/dt  + mr × dΩ/dt - 2mΩ × v - mΩ × (Ω × r).
  Here -mdV/dt = fictitious force due to acceleration of frame.
  mr × dΩ/dt = fictitious force due to non-uniform rotation of frame.
  -2mΩ × v = Coriolis force.
  -mΩ × (Ω × r) = Centifugal force.
  In the inertial frame we have
  F_inertial = mdv/dt + mdV/dt  - mr × dΩ/dt + 2mΩ × v + mΩ × (Ω × r).
• Details of the calculation:
  For our student dv/dt = dV/dt = 0.
  F_inertial = -mr × dΩ/dt + 2mΩ × v + mΩ × (Ω × r).
  In the inertial frame
  F_tangential = (mrα + 2mvαt),  F_rad = -m(αt)²r,
  F_tangential = 3mrα,  F_rad = -m(αt)²r.
  In the inertial frame the acceleration is therefore given by
  a_tangential = 3rα,  a_rad = -(αt)²r.
  Assume that the direction of Ω is the z-direction. 
  Then a_tangential = 3rα(ф/ф) and  a_rad = -(αt)²r.
  Transforming from polar to Cartesian coordinates we have
  (r/r) = cosф i + sinф j,  (ф/ф) = -sinф i + cosф j.
  Therefore a_x = -(αt)²cosф - 3rα sinф,  a_y = -(αt)²sinф + 3rα cosф.
  r = vt, ф = ½αt².
  a_x = -(αt)²cos(½αt²) - 3vtα sin(½αt²),  a_y = -(αt)²sin(½αt²) + 3vtα cosф(½αt²).

Problem:

On the surface of the earth an object is given an initial speed v on a friction less surface at latitude λ.  Show that the object will move in a circle and find the radius of the circle for velocities small enough that the radius is much smaller than the earth radius.

Solution:

• Concepts:
  Motion in an accelerating frame
• Reasoning:
  
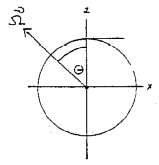
  Assume an observer at mid latitudes λ = 90^o - θ.
  The object is observed by an observer in a uniformly rotating coordinate system.
  The equations of motion in a rotating coordinate system contain fictitious forces.
  mdv/dt = F_inertial - mΩ × (Ω × r) - 2mΩ × v = -mg + N - mΩ × (Ω × r) - 2mΩ × v.
  -mΩ × (Ω × r) = centrifugal force.
  -2mΩ × v = Coriolis force.
  The force of gravity and the radial component of the fictitious forces, giving mg_eff ≈ mg, are balanced by the force of constraint from the ground.
  Let the z-axis of the coordinate system point into the -g_eff direction.  The Coriolis force and the centrifugal force both have a component ⊥to the z-axis.
• Details of the calculation:
  Choose the coordinates as shown,
  F_coriolis⊥ = (2m Ω_z dy/dt) i - (2m Ω_z dx/dt) j.  Here Ω_z = Ωcosθ.
  F_{centrifugal⊥} = mΩ²Rsinθcosθ i = b i.
  (F_{centrifugal⊥} is responsible for the oblateness of the earth. It is therefore also balance by the normal force.)
  Neglecting F_{centrifugal⊥}, we have d²x/dt² = 2Ω_z dy/dt,  d²y/dt² = -2Ω_z dx/dt.
  dv_x/dt = 2Ω_zv_y,  dv_y/dt = -2Ω_zv_x.
  Solutions:  v_x = A cos(ωt + φ),  v_y = -A sin(ωt + φ),  ω = 2Ω_z.
  x = (A/(2Ω_z)) sin(2Ω_zt + φ), y = (A/(2Ω_z)) cos(2Ω_zt + φ).
  This is motion in a circle, clockwise when looking down on the northern hemisphere.
  Ω_z = (2π/day) cos(θ), v² = v_x² + v_y² = A², radius r = v/(2Ω_z).

Problem:

A particle moves in a horizontal plane on the surface of the Earth.  Show that the magnitude of the horizontal component of the Coriolis force is independent of the direction of the motion of the particle.

Solution:

• Concepts:
  Motion in an accelerating frame
• Reasoning:
  Assume an observer at mid latitudes.
  
  The object is observed by an observer in a uniformly rotating coordinate system.
  The equations of motion in a rotating coordinate system contain fictitious forces.
  mdv/dt = F_inertial - mΩ × (Ω × r) - 2mΩ × v = -mg + N - mΩ × (Ω × r) - 2mΩ × v
  -mΩ × (Ω × r) = centrifugal force
  -2mΩ × v = Coriolis force
  The radial terms sum to zero.  The force of gravity and the radial components of the fictitious forces, giving mg_eff ≈ mg, are balanced by the force of constraint from the ground.
  Choose the coordinate system as shown.  Let the z-axis of the coordinate system point into the -g_eff direction.  Then the Coriolis force has a component ⊥ to the z-axis.
• Details of the calculation:
  F_coriolis⊥  = (2m Ω_z dy/dt) i - (2m Ω_z dx/dt) j.  Here Ω_z = Ωcosθ.
  |F_coriolis⊥| = [(2m Ω_z v_y)² + (2m Ω_z v_x)²]^½ = 2m Ω_z v
  The magnitude of the horizontal component of the Coriolis force,  |F_coriolis⊥| = 2m Ω_z v, is independent of the direction of v.

Problem:

If a particle is projected vertically upward from a point on the earth's surface at northern latitude λ.  Find the magnitude and direction of its deflection due to the Coriolis force when it hits the ground in terms of the maximum height reached and g_eff.  Here g_eff is the acceleration due to gravity already corrected for the centrifugal force, g_eff = g + O(Ω²).  Neglect terms of order Ω² and air resistance, and consider only small vertical heights.

Solution:

• Concepts:
  Motion in an accelerating frame
• Reasoning:
  
  Assume an observer in the rotating frame at mid latitudes λ = 90^o - θ.
  The equations of motion in a rotating coordinate system contain fictitious forces.
  mdv/dt = F_inertial - mΩ × (Ω × r) - 2mΩ × v.
• Details of the calculation:
  mdv/dt = mg_eff - 2mΩ × v.
  dv_z/dt = -g_eff ,  dv_y/dt = 2Ω_xv_z.
  v_z(t) = v₀ - g_efft, v_y(t) = 2Ω_x∫₀^t(v₀ - g_efft')dt'
  = -2Ω sinθv₀t + Ω sinθg_efft².
  
  y(t) = ∫₀^tv_y(t')dt' = -Ω sinθv₀t² + Ω sinθg_efft³/3.
  v₀ = (2hg_eff)^½. t = 2(2h/g_eff)^½.
  
  deflection:  y(h) =  -8Ω sinθ(2h³/g_eff)^½ + 8Ω sinθ(2h³/g_eff)^½/3.
  
  y(h) = -(8/3)Ω sinθ(2h³/g_eff)^½, or
  y(h) = -(8/3)Ω cosλ(2h³/g_eff)^½,
  The object is deflected westward.
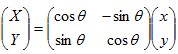