Newton's law of gravitation, Gauss' law

The gravitational force and potential energy

Problem:

Consider a rotating spherical planet. The speed of a point on its equator is V.  Particles near the surface of the planet accelerate downward (towards the center of the planet) with acceleration g' = ½g, where g is the downward acceleration of particles at the poles of the planet.  What is the escape velocity for a polar particle on the planet expressed as multiple of V?

Solution:

• Concepts:
  Newton's law of gravitation, centripetal acceleration
• Reasoning:
  The acceleration at the poles is the gravitational acceleration, the acceleration at the equator is the gravitational acceleration minus the centripetal acceleration.
• Details of the calculation:
  At the pole:  g = GM/R²
  At the equator:  g' = g/2 = GM/R² - V²/R
  Therefore g = 2V²/R.
  For a particle to escape from the planet, its total energy must be equal or greater than zero.  For a polar particle its minimum speed v (escape velocity) is found from
  ½mv² - GMm/R² = 0, v² = 2GM/R = 2gR = 4V².
  v = 2V.

Problem:

You are an astronaut and you observe a small planet to be spherical.  After landing on the planet, you set off, walk straight ahead, and find yourself returning to your spaceship from the opposite side after completing a lap of 25 km.  You hold a hammer and a falcon feather at a height of 1.4 m, release them, and observe them to fall together to the surface in 29.2 s.  What is the mass of the planet?

Solution:

• Concepts:
  Newton's law of gravitation, kinematics
• Reasoning:
  Near the surface of the planet the gravitational acceleration is constant, pointing downward.  Newton's law of gravitation, F = GMm/R² lets us calculate the magnitude of this acceleration as a function of the mass M and the radius R of the planet.  Walking around the planet yields its circumference, and given the circumference of the planet, therefore the radius R can be determined.  The acceleration g is measured by dropping the objects through a known distance and measuring the time interval ∆t.  The objects fall together, so we know there is no drag due to an atmosphere.
• Details of the calculation:
  ∆y = ½g∆t² yields g = 2*1.4 m/(29.2 s)²,
  2πR = 25 km, yields R = 25 km/2πg = GM/R²,  M = gR²/G = [2*1.4 m/(29.2 s)² * (25 km/2π)²/(6.67 10^-11m³kg^-1s^-2) = 7.8 10¹⁴ kg

Problem:

An expedition of space treasure hunters discovered a remote spherical planet made of pure gold with density ρ = 19.3*10³ kg/m³.  The expedition circled the planet and decided to come back later.  Upon their return, they were astonished to find that someone had sliced off exactly half of the planet, leaving a perfect hemisphere.  The treasure hunters landed at the center of the flat surface of the remaining hemisphere and discovered that the acceleration due to gravity there was the same as that on the surface of the Earth.  Help the treasure hunters determine the radius of the planet and the acceleration due to gravity on the surface before it was sliced in half.

Solution:

• Concepts:
  Newton's law of gravitation
• Reasoning:
  We need to find the gravitational field at the center of the flat surface of the hemisphere of uniform density ρ and radius R. 
• Details of the calculation:
  Choose the coordinate system so that the flat surface lies in the xy-plane with its center at the origin and z  ≥ 0 for all points on the hemisphere.
  For a shell of radius r and thickness dr of this hemisphere, the gravitational field  F/m at the center points in the z-direction, from symmetry.  For such a shell we have
  |F/m| = ρG2πr²dr∫₀^π/2sinθcosθdθ/r² = ρG2πdr∫₀^π/2sinθcosθdθ = ρG2πdr/2= ρGπdr.
  Integrating rom r = 0 to r = R we find F/m = g_hemisphere =  ρGπR k at the center of the hemisphere.
  Therefore
  R = g_hemisphere/(ρGπ) = (9.8 m/s²)/(π*19.3*10³ kg/m³*6.67*10^-11 N m²/kg²) = 2.42*10⁶ m.
  The acceleration due to gravity on the surface before the planet was sliced in half was
  g_planet = GM/R = (4/3)πRρG = (4/3)* 9.8 m/s² = 13.1 m/s².

Problem:

Use the principle of conservation of mechanical energy to find the velocity with which a body must be projected vertically upward, in the absence of air resistance, to rise to a height above the earth's surface equal to the earth's radius, R.

Solution:

• Concepts:
  Conservation of mechanical energy, Newton's law of gravity
• Reasoning:
  The gravitational force is a conservative force.
  Initial energy:  ½mv² - GmM_E/R.
  Final energy:  -GmM_E/(2R).
• Details of the calculation:
  Energy conservation:  ½mv² - GmM_E/R = -GmM_E/(2R),  v = (GM_E/R)^1/2 = 7.9*10³ m/s.

Problem:

Suppose the Moon were to have the same mass as the Earth, and you are trying to throw one of your physics books from the Earth to the Moon.  With what minimum velocity must the book leave the surface of the Earth?  Neglect the relative motion of the Earth and them Moon, and the Earth's rotation.  The mass of the Earth is M_E = 6.0*10²⁴ kg, the radius of the Earth is R_E = 6.4*10⁶ m, and the distance from the center of the Earth to the center of the Moon is R_EM = 3.8*10⁸ m.  Compare your answer to the escape velocity from Earth alone.  The gravitational constant is G = 6.67*10⁻¹¹ N m²/kg².

Solution:

• Concepts:
  Newton's law of gravitation, conservation of energy
• Reasoning:
  The gravitational field is a conservative field.
• Details of the calculation:
  Let the book have mass m.  The potential energy of the book measured along a line joining the earth and the moon a distance r away from the earth is
  U(r) = -GM_Em/r - GM_Em/|R_EM - r|.
  It has a local maximum at r = R_EM/2.  The book needs enough kinetic energy to overcome this barrier.
  We need ½mv² - GM_Em/R_E - GM_Em/|R_EM - R_E| = -GM_Em/(½R_EM) - GM_Em/(½R_EM).
  v² = 2GM_E(1/R_E + 1/|R_EM - R_E| - 4/R_EM), v = 10.9 km/s.
  For the book to escape from the earth alone we need ½mv² - GM_Em/R_E = 0,
  v = 11.2 km/s.

Problem:

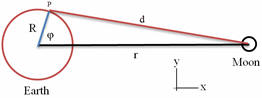
The tidal force ΔF_φ/m of the Moon on the Earth is defined as the difference between the gravitational field of the Moon at a point on the Earth's surface defined by the angle φ and the gravitational field of the Moon at the Earth's center.  (See figure.)  Derive an expression for ΔF_φ/m.  Simplify by assuming that R, the radius of the Earth, is much smaller than r, the Earth-Moon distance.
Find the x- and y components and the tangential and radial components of ΔF_φ/m.

Solution:

• Concepts:
  Newton's law of gravity
• Reasoning:
  From geometry:
  At the point P  ΔF_φ/m = (GM/d² )(e_x(r - Rcosφ)/d - e_y(Rsinφ)/d)  - (GM/r²)e_x)
  Here M is the mass of the moon.
  d² = (r - Rcosφ)² + (Rsinφ)² = r² + R² - 2rRcosφ
• Details of the calculation:
  ΔF_φ/m = (GM/(r² + R² - 2rRcosφ)^3/2)[e_x(1 - (R/r)cosφ) - e_y(R/r)sinφ)]  - (GM/r²)e_x
  = -(GM/r²))e_x[(1 - (R/r)cosφ)/(1 + R²/r²- 2(R/r)cosφ)^3/2  -1]
  -(GM/r²))e_y(R/r)sinφ)/(1 + R²/r²- 2(R/r)cosφ)^3/2
  Since r << R, we expand and neglect terms higher than first order in R/r.
  ΔF_φ/m = (GM/r²))e_x[(1 - (R/r)cosφ)/(1 - 3(R/r)cosφ)  - 1]
  -(GM/r²))e_y(R/r)sinφ) 
  (ΔF_φ/m)_x = (GM/r²)[(1 - (R/r)cosφ)/(1 - 3(R/r)cosφ)  - 1] = (2GMR/r³)cosφ
  (ΔF_φ/m)_y = -(GMR/r³)sinφ
  We have azimuthal symmetry about the x-axis.
  (ΔF_φ/m)_tangential = (ΔF_φ/m)_xsinφ - (ΔF_φ/m)_ycosφ = (GMR/r³)3cosφ sinφ = (GMR/r³)(3/2) sin(2φ)
  A positive (ΔF_φ/m)_tangential points clockwise.
  (ΔF_φ/m)_radial = (ΔF_φ/m)_xcosφ + (ΔF_φ/m)_ysinφ = (GMR/r³)(2cos²φ - sin²φ)
  = (GMR/r³)(2 - 3sin²φ) = ½(GMR/r³)(1 + 3sin(2φ)).

Problem:

Consider a neutron star, a macroscopic body composed of neutrons, at a density ρ = 10¹⁷ kg/m³. The temperature of the star's interior is approximately 10⁷ K.  For this problem, consider the star to be a non-interacting Fermi gas of neutrons.
For an ideal non-relativistic 3D Fermi gas comprising N non-interacting fermions, the Fermi energy (the energy difference between the highest and lowest occupied single-particle states at T = 0) is given by E_F = [ħ²/(2m)](3Nπ²/V)^2/3, and the average energy per fermion at absolute zero <E> = (3/5) E_F.
(a)  Determine the Fermi energy of the neutrons in the neutron star.  Are the neutrons relativistic or nonrelativistic?
(b)  Determine whether or not the neutrons are reasonably well considered to be a zero temperature (E_F >> kT) Fermi gas.
(c)  Estimate the pressure in the neutron star P = -∂U/∂V.  (quasi-static, adiabatic, fixed # of particles)  In equilibrium this pressure balances the pressure due to gravity.
(d)  Use (c) to estimate the mass of this neutron star.

Solution:

• Concepts
  Fermi energy, thermodynamic pressure, gravitational pressure
• Reasoning:
  For a T = 0 Fermi gas P = -∂U/∂V = -N∂<E>/∂V = (3/5)N ∂E_F/∂V.
• Details of the calculation:
  (a)  E_F = [ħ²/(2m_n)](3Nπ²/V)^2/3.
  N/V = ρ/m_n = (10¹⁷ kg/m³)/(1.67*10^-27 kg).
  E_F ≈ 5*10^-12 J,  kT = 1.38*10^-23*10⁷ J ≈ 10^-16 J, m_nc² = 1.5*10^-10 J.
  m_nc² >> E_F >>kT.  The neutrons are nonrelativistic.
  (b)  E_F >> kT, the neutrons are reasonably well considered to be a zero temperature Fermi gas.
  (c)  dU = -PdV for a gas isolated from is environment.
  P = -∂U/∂V.  U = N<E> = (3/5)N E_F.
  P = (2/3)(3/5) N E_F/V = (2/5) N E_F/V = [ħ²/(5m_n)](3π²)^2/3(N/V)^5/3
  = [ħ²/(5m_n^8/3)](3π²)^2/3ρ^5/3.
  (d)  The gravitational energy of the neutron star is
  E_g = -∫₀^RGM_inside4πr²ρdr/r = -∫₀^RG(4πr³ρ/3)4πr²ρdr/r = -(4π)²Gρ²R⁵/15 = -3GM²/(5R).
  E_g = -(3/5)G(Nm_n)²(4π/3)^(1/3)V^-(1/3).
  P_g = -∂E_g/∂V = -(1/5)G(Nm_n)²(4π/3)^(1/3)V^-4/3 = -(1/5)Gρ²(4π/3)R².
  P_g + P = 0 in equilibrium.
  [ħ²/(5m_n^8/3)](3π²)^2/3ρ^5/3 - (1/5)Gρ²(4π/3)R² = 0.
  [ħ²/m_n^8/3]3^5/3π^(1/3) = 4Gρ^(1/3)R².
  R = 1.4*10⁴ m = 14 km.
  M = (10¹⁷ kg/m³)(4πR³/3) ≈ 10³⁰ kg, on the order of the mass of the sun.

Gauss' law

Problem:

Assuming that the earth is a uniformly dense sphere and that the acceleration of gravity is g at the surface, what is the acceleration of gravity below the surface as a function of distance from the center?

Solution:

• Concepts:
  Newton's law of gravitation, Gauss' law
• Reasoning:
  The gravitational acceleration a distance r from the center is in the -r direction and its magnitude is found using "Gauss' law".
• Details of the calculations:
  Imagine a tunnel bored through the center of the earth.  For a test particle a distance r from the center we have
  (1/m)∫_{closed area}F∙n dA = 4πGM_inside,
  F4πr² = m4πG(4/3)πr³ρ,  F = (4/3)Gmπρr,  a = (4/3)Gπρr.
  At the surface g = (4/3)GπρR, so a = gr/R, where R is the radius of the earth

Problem:

Imagine a tunnel bored through a homogeneous spherical Earth with radius R and mass M.  Suppose a particle is dropped from the surface into the tunnel.  Find its motion.

Solution:

• Concepts:
  Newton's law of gravitation, Gauss' law
• Reasoning:
  The particle is moving in an inertial frame.  The acceleration of the particle is due to the gravitational force.
  Assume a tunnel is bored through the center of the Earth.  The gravitational force on a test particle of mass m in the tunnel, a distance r from the center is in the -r direction and its magnitude is found using "Gauss' law".
• Details of the calculation:

  (1/m)∫_{closed area}F∙n dA = 4πGM_inside,

  F4πr² = m4πG(4/3)πr³ρ,  F = (4/3)Gmπρr.

  For a particle moving in the tunnel we therefore have F = -kr, k =( 4/3)Gmπρ.
  The force on the particle obeys Hooke's law.  The particle will oscillate with angular frequency ω = (k/m)^½ = ((4/3)Gπρ)^½.
  Its period is T = 2π/ω = (3π/Gρ)^½.

Problem:

Use Newtonian gravity to derive an expression for the time to collapse a spherical mass distribution if the only force acting is gravity (the dynamical or free-fall timescale).  Use this result to estimate the expected response time of the Sun to a significant gravitational disturbance, given that the radius of the Sun is about 7*10⁵ km and its mass is about 2*10³⁰ kg.

Solution:

• Concepts:
  Newton's law of gravitation, Gauss' law, energy conservation
• Reasoning:
  The gravitational acceleration a distance r from the center is in the -r direction and its magnitude is found using "Gauss' law".
  The gravitational force is a conservative force.
• Details of the calculation:
  The gravitational force per unit mass (acceleration) of a mass element dm at a radius r is
  g(r) = Gm_enc(r)/r².  Here m_enc(r) is the mass inside a sphere of radius r.
  The gravitational force is conservative.
  If the star collapses, a spherical shell of mass m_s originally at r₀ with m_enc(r₀) = m₀ has kinetic energy ½mv² = Gm₀m_s/r - Gm₀m_s/r₀ at r < r₀.
  (The change in gravitational potential energy is -∫_r0^r F(r) dr = -∫_r0^r m₀g(r) dr = Gm₀m_s/r₀ - Gm₀m_s/r.)
  Its speed is v(r) = dr/dt = -(2Gm₀(1/r - 1/r₀))^½.
  For this shell the time to collapse is t = ∫_r0⁰(dt/dr)dr = ∫₀^r0dr/(2Gm₀(1/r - 1/r₀))^½.
  t = (2Gm₀)^-½∫₀^r0dr/(1/r - 1/r₀))^½ = (r₀³/2Gm₀)^½∫₀¹dx(x/(1 - x))^½ = (r₀³/2Gm₀)^½(π/2).
  3m₀/(4πr₀³) is the initial density ρ of the spherical mass distribution.
  Therefore we can write t = (3π/(32*G ρ)^½.  t is independent of r₀, the whole mass just contacts.
  Assume that 3m₀/(4πr₀³) is approximately equal to the average density of the sun,
  ρ_avg = 3*2*10³⁰ kg/(4π*(7*10⁸ m)³) = 1.4*10³ kg/m³.
  Then t = (3π/(32*G ρ_avg))^½ ~ 1.8*10³ s.

Problem:

The shortest way from the US to Australia is via a tunnel that goes thought the center of the Earth.  If one could build such a tunnel and make it friction free, then an object dropped at the US side with zero initial velocity would emerge after some time on the other side in Australia.  Assuming that density of the Earth is uniform (which is not correct), calculate how long it would take for an object to pass through such a tunnel. 

Solution:

• Concepts
  Newton's law of gravitation, Gauss' law
• Reasoning:
  The gravitational acceleration a distance r from the center is in the -r direction and its magnitude is found using "Gauss' law".
• Details of the calculations:
  Imagine a tunnel bored through the center of the earth.  For a test particle a distance r from the center we have

  (1/m)∫_{closed area}F·n dA = 4πGM_inside,

  F4πr² = m4πG(4/3)πr³ρ,  F = (4/3)Gmπρr = ma, a = (4/3)Gπρr.
  At the surface g = (4/3)GπρR, so a = gr/R, where R is the radius of the earth.

  F = -(mg/R)r.
  If the coordinate system is chosen so that the origin is at the center of the Earth and the tunnel lies along the y-axis, then F = -(mg/R)y.
  y = Rcos(ωt), ω = (g/R)^1/2 = 2π/T,  T/2 = (Rπ²/g)^1/2 is the time it take to pass through the tunnel.  T/2 = 2535 s.

Problem:

At larger distances from the center of the spiral galaxies, the rotation curve appears to be flat (the orbital speed is independent of the distance from the center).  This behavior is attributed to the peculiar distribution of the "dark mater"​.  Assume that the distribution of dark matter is independent of θ and Φ and calculate the radial density distribution of dark matter, which produces such a flat rotation curve.

Solution:

• Concepts:
  The gravitational force, Gauss' law: 
• Reasoning:
  4πR²F/m = 4πGM_inside, for a spherically symmetric mass distribution.
• Details of the calculation:
  v²/R = F/m = GM_inside/R²,   M_inside = Rv²/G. 
  If v = constant for large R, then dM_inside = ρ(R)4πR²dR = (v²/G)dR. 
  Then ρ(R) = v²/(4πGR²) for large R.