Chains

Problem:

A rope of length l slides over the edge of a table.  Initially a piece x₀ of it hangs without motion over the side of the table.  Let x be the length of rope hanging vertically at time t.  The rope is assumed to be perfectly flexible.
Show that E = T + U is a constant of motion.

Solution:

• Concepts:
  Conservation of mechanical energy
• Reasoning:
  We are asked to show that the mechanical energy is conserved in a given situation.
  • Why do we expect mechanical energy to be conserved in this situation?
    The only external forces acting are gravity on the vertical part of the rope and the normal force and gravity on the horizontal part of the rope.  Gravity is a conservative force and the normal force acts perpendicular to the velocity and therefore does no work.
• Details of the calculation:
  Let l be the length of the rope, ρ its mass  per unit length, and let x be the part hanging over the edge.
  
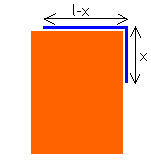
  This is an effectively one-dimensional problem.  The picture below shows a blow-up of the corner, the section of the rope bending around the corner has infinitesimal length.
  
  
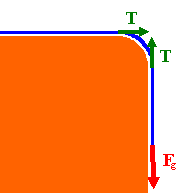
  F_g - T = d(ρxv)/dt for the vertical part of the rope, T = d(ρ(l-x)v)/dt for the horizontal part of the rope.
  Defining p = ρlv = ρldx/dt we have  F_g = dp/dt =  ρld²x/dt² = ρgx.
  d²x/dt² = gx/l.
  T = ½ρl(dx/dt)²,  U = -ρg(x²/2),  E = T + U = ½ρl(dx/dt)² - ρg(x²/2)
  dE/dt = ρl(dx/dt)d²x/dt² - ρgxdx/dt = ρgxdx/dt - ρgxdx/dt = 0.

Problem:

A chain lies pushed together at the edge of a table, except for a piece which hangs over it, initially at rest.  The links of the chain start moving, one at a time.
Show that E = T + U is not a constant of motion.

Solution:

• Concepts:
  Non-conservation of mechanical energy in inelastic processes
• Reasoning:
  We are asked to show that the mechanical energy is not conserved in a given situation.
  • Why do we expect mechanical energy to not be conserved in this situation?
    
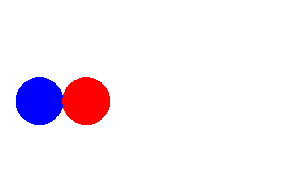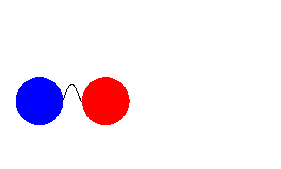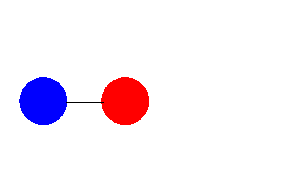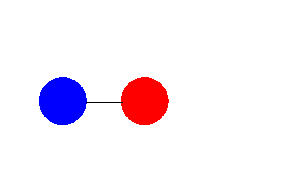
    Consider two adjacent links of the chain.  Link 1 (red) moves away from link 2 (blue).  Initially the two links do not interact.  After link 1 has traveled a distance Δx, it interacts with link 2 (blue) and the two links stick together and move together.  The two links "collide" inelastically.  In an inelastic collision mechanical energy is not conserved.
• Details of the calculation:
  Let ρ its mass  per unit length of the chain.  Let l be the length of the chain that hangs over the edge.  This part of the chain is moving.  Let the x-axis point downward and let the tabletop be at x = 0.
  p_x = ρlv = ρldl/dt.  F_x = dp_x/dt =  ρ(dl/dt)² +  ρld²l/dt² = ρlg.
  T = ½ρlv² = ½ρl(dl/dt)²,  U = -ρlg(l/2),
  E = T + U = (ρl/2)[(dl/dt)² - gl].
  dE/dt = (ρ/2)(dl/dt)³ + ρl(dl/dt)d²l/dt² - ρgldl/dt.
  d²l/dt² = g - (1/l)(dl/dt)², from F_x = dp_x/dt.
  dE/dt = (ρ/2)(dl/dt)³ + ρlg(dl/dt) - ρ(dl/dt)³- ρgldl/dt = -(ρ/2)(dl/dt)³ = -(ρ/2)v³ ≠ 0.

Problem:

A butcher is holding a long string of small-link sausages upright just above the scale pan.  She offers to charge the costumer for just ½ of the maximum reading of the scale after she releases the string.  The customer eagerly agrees.  What percentage of the regular charge does the customer pay?

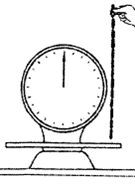
Solution:

• Concepts:
  Newton's 2nd law, F = dp/dt
• Reasoning:
  Let the mass of the string of sausages be m, its length be L, and let λ = m/L.  Consider the string to consist of sections of length dx.  After the string has fallen a distance x, the sections that have not yet reached the table have velocity v = (2gx)^½.  The scale has to support a section of the string of length x and has to reduce the momentum of a section of length dx from λdxv to zero in a time interval dt.
• Details of the calculation:
  The scale has to exert a force F = λxg + λv² in the upward direction.
  F = λxg + λ2gx = 3λxg.
  The maximum force is exerted when the last link is stopped by the scale.  F_max = 3λLg = 3mg.
  ½F_max = 1.5 mg.  The customer pays 150% of the regular charge.

Problem:

A uniform, dense rope of length b and mass per unit length m is coiled on a smooth table.  You lift one end of the rope by hand vertically upward at constant speed u₀.  Find the force that you must apply to the rope when the end is a distance a above the table (a < b). 

Solution:

• Concept:
  Newton's 2nd law, F = dp/dt
• Reasoning:
  Let a be the distance of the end of the rope above the table.  Consider the rope to consist of sections of length dx.  To move the rope upward with constant speed, you must apply an upward force equal to the force of gravity on the section of length a in addition to a force to change the momentum of a section dx from 0 to mdxu₀ in a time interval dt.
• Details of the calculation:
  F =  mag + m(dx/dt)u₀ = mag + mu₀².

Problem:

A uniform heavy chain of mass λ per unit length hangs vertically so that the low end just touches a horizontal table.  The upper end is released and the chain falls on the table.  Find the force the chain exerts on the table after it has fallen a distance x.

Solution:

• Concepts:
  Impulsive forces, Newton's 2nd law, F = dp/dt
• Reasoning:
  Consider the chain to consist of sections of length dx.  After the chain has fallen a distance x, the sections that have not yet reached the table have velocity v = (2gx)^½.
  The table has to support a section of the chain of length x and has to reduce the momentum of a section of length dx from λdxv to zero in a time interval dt.
• Details of the calculation:
  The table has to exert a force F = λxg + λv² in the upward direction.
  F = λxg + λ2gx = 3λxg.

Problem:

A rope of mass M and length L is suspended in the earth's gravitational field, g, with the bottom end of the rope touching a surface.  The rope is released from rest and falls limply on the surface, without bouncing.  Find the force F(t) exerted on the surface as a function of time.  At what time does F(t) reach its maximum?  What is the magnitude of this maximum force?

Solution:

• Concepts:
  Newton's 2nd law, F = dp/dt
• Reasoning:
  Let  λ = M/L.  Consider the rope to consist of sections of length dx.  After the rope has fallen a distance x = ½gt², the sections that have not yet reached the table have velocity v = (2gx)^½.  The scale has to support a section of the rope of length x and has to reduce the momentum of a section of length dx from λdxv to zero in a time interval dt.
• Details of the calculation:
  The scale has to exert a force F = λxg + λv² in the upward direction.
  F = λxg + λ2gx = 3λxg.  F(t) = (3/2)(M/L)g²t² for t < T = (2L/g)^½.
  The maximum force is exerted when the last link is stopped by the scale.  F_max = 3λLg = 3Mg at t = T.
  For t > T we have F = Mg.

Problem:

A rope with mass M and length L is held in the position shown below, with one end attached to a support. (Assume that only a negligible length of the rope starts out below the support.) The rope is released. Find the force that the support applies to the rope, as a function of time.

Solution:

• Concepts:
  Newton's second law
• Reasoning:
  At time t, the free end of the rope is moving at speed gt, and it has fallen a distance gt²/2.  This distance gets "doubled up" below the support.  So at time t, a length gt²/4 is hanging at rest, and a length L - gt²/4 is moving at speed gt. The momentum of the entire rope is therefore p = - λ(L - gt²/4 )gt, where λ is the mass per unit length of the rope.  The minus sign signifies downward motion.  The forces on the entire rope are Mg = λLg downward, and N (the force from the support) upward.
• Details of the calculation:
  F = dp/dt applied to the entire rope gives
  N - λLg = d/dt(- λ(L - gt²/4 )gt) = - λLg + 3λg²t²/4.
  N = 3λg²t²/4.
  or:
  N must support a section of length a length x = gt²/4 and must change the momentum of a section dx = 2gtdt/4 from λdxgt to zero.  dp = 2λg²t²dt/4,  dp/dt = 2λg²t²/4. 
  N = λg²t²/4 + 2λg²t²/4 = 3λg²t²/4.

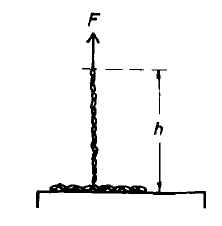
Problem:

A chain with mass/length = m hanging vertically from one end, where an upward force F is applied to it, is lowered onto a table as shown in the figure.
Find the equation of motion for h, the height of the end above the table (h is the length of chain hanging freely).

Solution:

• Concepts:
  Newton's 2nd law, F = dp/dt
• Reasoning:
  In addition to the applied and gravitational forces, we have to take into account the impulse due to a section of the chain being stopped by the table.
• Details of the calculation:
  
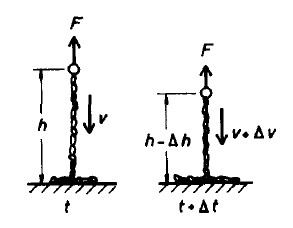
  For this one-dimensional problem let the downward direction be the positive direction.
  The change in momentum of the chain in a time interval dt is
  dp = m(h - dh)(v + dv) - mhv = m h dv - m dh v,
  keeping only first order terms.
  dp/dt = m h dv/dt - m dh/dt v =  m h dv/dt - m v²,
  We also have
  dp = -Fdt  + m h g dt - m dh v,  where mdhv is the impulse due to a section of the chain being stopped by the table.  This impulse is provided by the normal force from the table.
  dp/dt = -F + mhg - m v².
  Combining:  dv/dt = -(F - mhg)/(mh).  dv/dt = -d²h/dt².  d²h/dt² = F/(mh) - g.

Problem:

A ball of mass M on a frictionless horizontal table is pulled by a constant horizontal force F.  A coiled up rope of mass per unit length r is attached which uncoils as the body moves. 
(a)  By taking into account the uncoiling of the rope, derive an expression for the speed of the ball as a function of distance traveled.
(b)  Evaluate the terminal speed of the ball, assuming a very long rope.

Solution:

• Concepts:
  Newton's 2nd law, F = dp/dt
• Reasoning:
  F = dp/dt, yields the equations of motion, which can be solved for the velocity as a function of position.
• Details of the calculation:
  (a)  F  = dp/dt. (1-dimensional problem)
  p = mv = (M + m_rope)v, dp = vdm_rope + mdv.  dm_rope = rdx,  m = M + rx.
  F = rv² + (M + rx)dv/dt.
  We are interested in dv/dx.
  dv/dt = (dv/dx)v.  vdv/dx = (F - rv²)/ (M + rx).
  Let x' = (M + rx), then dx' = rdx.
  vdv/dx' = (F/r- v²)/x'.  Let F/r = B.
  vdv/dx' = (B - v²)/x', dv²/dx' = 2B/x' - 2v²/x' = 2(B - v²)/x'.
  Let v'² = -v².  Then dv'²/dx' = -2v'²/x'.
  v'² = C₁/x'².  dv'²/dx' = -2C₁/x'³ = -2v'²/x'.  v² = F/r  - C₁/x'².
  The initial conditions are v² = 0 and x' = M.
  Therefore C₁ = M² F/r.
  v²(x) = (F/r)(1  - M²/(M + rx)²).
  (b)  As x--> infinity, v² --> F/r.

Problem:

A uniform chain of length 4l and mass density ρ is held so half of it is coiled up in a heap at the edge of a smooth table while the other half is hanging as shown.  It is supported at a point A, which is at the same vertical height as the table.

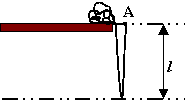
The chain is released from rest.
(a)  Show that just after the last link leaves the table its speed is v = (31/20)^½(gl)^½.
You may assume that all motion occurs along a single vertical line.
(b)  What force is exerted on the chain at point A, immediately prior to the instant when the chain first becomes vertical?

Solution:

• Concepts:
  Newton's 2^nd law
• Reasoning:
  The system consists of the part of the chain that is coiled up, the part that is falling, and the part that is hanging at rest.  In a small time interval dt the momentum of the system changes because a small amount dm₁ of the coiled up chain receives an impulse dm₁v and starts falling, a small amount of the falling chain dm₂ receives an impulse -dm₂v and stops falling and the section m that is falling speeds up (mdv).  The forces acting on the uncoiled parts of the chain are gravity and the force from the support.
• Details of the calculation:
  (a) Δp = (m + Δm)(v + Δv) - mv,  dp = mdv + vdm.
• Let us picture each link of the chain as a box.
  
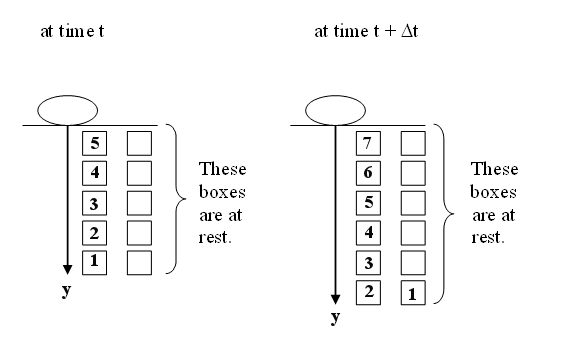
  At time t:  p = ρyv.  dp = ρydv/dt + vρdy.
  dp/dt = ρy(dv/dt) + ρv(dy/dt).  dy/dt = v/2.
  The falling links travel a distance equal to the length of two links while the length of the chain y only increases by the length of one link.
  The force on the part of the chain that is not coiled up is
  F = 2ρyg - F_s (gravity + force from the support).
  Let F_s = F₁ + ρyg.  F₁ provides the impulse that stops dm₂. 
  F₁ = ρ(dy/dt)v = ρv²/2.
  F = dp/dt = ρyg - F₁.  ρy(dv/dt) + ρv²/2 = ρyg - ρv²/2.  ydv/dt + v² = yg.
  We want to solve this differential equation for v(y).  We want to find v(2l).  We have to eliminate t from the equation.
  dy/dt = v/2.  d/dt = (v/2)d/dy.  y(v/2)dv/dy + v² = yg.  (y/4)dv²/dy + v² = gy.
  dv²/dy = -4v²/y + 4g.
  Try v² = ay + b/y⁴.  Then dv²/dy = a - 4b/y⁵ = -4v²/y + 5a.  Therefore a = 4g/5.
  v²(l) = 0 --> al + b/l⁴ = 0, b = -al⁵.
  v²(2l) = a2l - al⁵/(16l⁴) = al(2 - 1/16) = al*31/16 = gl*31/20.
  
  (b)  Assume the last link has left the table.  Look at the chain at some time t when a section is falling and a section is hanging at rest.
  
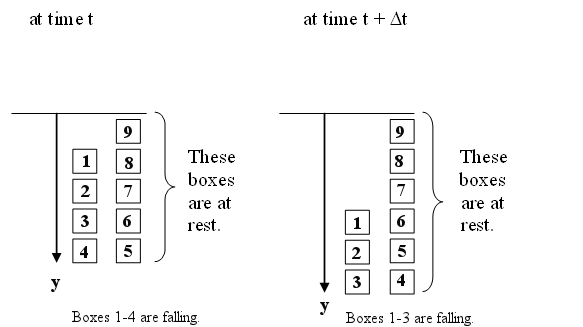
  p = ρ(y - y₁)v,  dp = mdv + vdm = ρ(y - y₁)dv + ρv(dy - dy₁)
  dp/dt = ρvdy/dt - ρvdy₁/dt  + ρ(y - y₁)dv/dt.
  dy/dt = v/2,  dy₁/dt = v.
  F = ρ(y - y₁)g - F₁ = ρ(y - y₁)g - ρv²/2.
  F = dp/dt --> ρ(y - y₁)g - ρv²/2 = -ρv²/2  + ρ(y - y₁)dv/dt.
  dv/dt = g, dy/dt = v/2, (v/2)dv/dy = g, dv²/dy = 4g.
  v²(4l) - v²(2l) = 4g*2l = 8gl.
  v²(4l) = gl*31/20 + 8gl = 191/20.
  F₁(4l) = ρv²(2l)/2 = ρgl*191/40.
  F_s = ρ4gl + ρgl*191/40 = ρgl*351/40 = total force exerted by the support.