Elastic collisions
Problem:
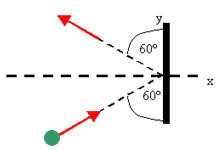
A 3 kg steel ball strikes a wall with a speed of 10.0 m/s at an angle of 60o
with the surface. It bounces off with the same speed and angle.
If the ball is in contact with the wall for 0.2 s, what is the average force
exerted on the ball by the wall?
Solution:
- Concepts:
Impulse: dp =
Fdt, ∆p =
Favg∆t
- Reasoning:
In the elastic collision with the "infinitely" massive wall, the ball receives
an impulse ∆p. Enough information is given to calculate ∆p.
Since the contact time is given, Favg can be calculated.
- Details of the calculation:
The balls initial momentum is
pi
= pxii + pyij
= (3 kg 10 m/s)sin60oi
+ (3 kg 10 m/s)cos60oj.
Its final momentum is
pf = pxfi + pyfj
= -(3 kg 10 m/s)sin60oi
+ (3 kg 10 m/s)cos60oj.
∆p
= pf
- pi= -2(30 kgm/s)sin60oi
= -(51.96 kgm/s)i.
∆p =
Favg ∆t.
Favg
= -(51.96 kgm/s)i/(0.2s) = -259.8 Ni.
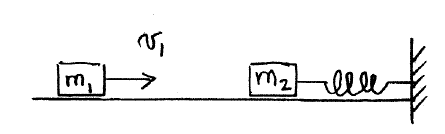
Problem:
A block of mass m1 and initial velocity v1 collides
head-on with a stationary block of mass m2. The mass m2
compresses a spring of spring constant k. Neglect friction and assume the
collision is elastic.
(a) What is the velocity v2' of m2 just after the
collision?
(b) What is the maximum compression of the spring?
Solution:
- Concepts:
Elastic collisions, energy and momentum conservation
- Reasoning:
In elastic collisions energy and momentum are conserved.
- Details of the calculation:
(a) Let v1'and v2' be the velocities of m1
and m2 just after the collision.
Momentum conservation: m1v1 = m1 v1'
+ m2 v2'.
Energy conservation: m1v12 = m1
v1'2 + m2 v2'2.
v2' = 2v1/(1 + m2/m1).
(b) ½m2v2'2 = ½kd2, where d is
the maximum compression of the spring
d = (m2/k)½2v1/(1 + m2/m1).
Problem:
A (non-relativistic) neutron in a reactor makes an elastic head-on collision with the nucleus of
a carbon atom initially at rest.
(a) What fraction of the neutron's kinetic
energy is transferred to the carbon nucleus?
(b) If the initial kinetic
energy of the neutron is 1.6*10-13 J, find its final kinetic energy
and the kinetic energy of the carbon nucleus after the collision.
(The mass
of the carbon nucleus is about 12 times the mass of the neutron.)
Solution:
Problem:
A non-relativistic neutron with mass m and kinetic energy T scatters elastically
off a nucleus with mass M. What is the maximum kinetic energy that can be
transferred to the nucleus in one collision if
(a) M is initially at rest,
(b) or M is initially allowed to move?
Solution:
- Concepts:
Elastic collisions, energy and momentum conservation
- Reasoning:
The maximum kinetic energy is transferred in a head-on collision. We use
energy and momentum conservation.
- Details of the calculation:
(a) If M is at rest and m = m1, M = m2.
Momentum conservation:
(i) m1v1i = m1v1f + m2v2f.
Energy conservation:
(ii) ½m1v1i2 = ½m1v1f2
+ ½m2v2f2
v2f2 = (m1/m2)(v1i2
- v1f2) from (ii),
v1f = v1i - (m2/m1)v2f
from (i).
We can therefore write
v1f2 = v1i2 + (m2/m1)2v2f2
- 2(m2/m1)v1iv2f.
v2f2 = (m1/m2)( 2(m2/m1)v1iv2f
- (m2/m1)2v2f2) = 2v1iv2f
- (m2/m1)v2f2.
(1 + (m2/m1))v2f = 2v1i.
v2f = 2m1v1i/(m1+m2).
The maximum amount of kinetic energy transferred is ½Mv2f2
= [4mM/(M+m)2]T.
(b) If M is allowed to move, then the maximum amount of kinetic energy
transferred is T, and m is at rest after the collision.
(For this to happen M must initially moves with speed ½(1 - m/M)v into the
same direction as m.)
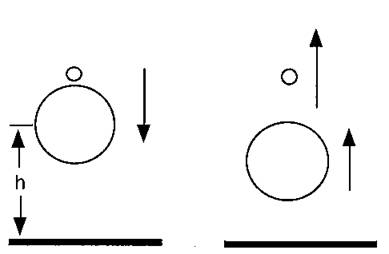
Problem:
Two perfectly elastic balls, the larger of mass M and the smaller of mass m,
with m << M, are dropped from a height h >> radius of either ball above a solid
surface. Mass M rebounds elastically from the surface and mass m rebounds
elastically from M. Find the height H that the small ball reaches in terms
of h. You need only find an approximate result in the limit that m/M -->
0. The general result depends upon the ratio m/M.
Solution:
- Concepts:
Elastic collisions, frame transformations
- Reasoning:
When an object of mass m1 << m2
and velocity v collides head on with an object of mass m2
at rest, then m1 rebounds with a velocity nearly equal to -v.
- Details of the calculation:
Assume M collides with velocity
v = -(2gh)½
j
= -vj with the ground. It rebounds with velocity vj. In a
frame moving with velocity vj equal to the velocity of M right after
the collision with the ground, m approaches with velocity -2vj and
rebounds with velocity 2vj. In the lab frame m moves with velocity
3vj = (2gh')½
j right after its collision with M,
and therefore rises to a height of h' = 9h.
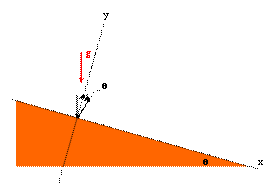
Problem:
An elastic ball is dropped on a long inclined plane. It
bounces, hits the plane again, bounces, and so on. Let us label the
distance between the points of the first and the second hit d12
and the distance between the points of the second and the third hit d23.
Find the ratio d12/d23.
Solution:
- Concepts:
Elastic collisions, motion with constant acceleration
- Reasoning:
The component of the acceleration perpendicular to the inclined plane and
the component of the acceleration parallel to the inclined plane are
constant. The balls motion perpendicular to the inclined plane is a
series of bounces from some initial height above the plane to the plane and
back to the initial height. The time interval between successive
contacts with the plane is constant. But the ball also accelerates in
the direction parallel to the plane, so the distance along the plane between
successive contacts with the plane increases.
- Details of the
calculation:
Assume the inclined plane makes an angle
θ with the horizontal. Orient the axes
of your coordinate system as shown in the figure. The x-axis makes an
angle θ with the horizontal and the
y-axis is perpendicular to the inclined plane. The ball is dropped vertically
and just after the first bounce its velocity vector makes an angle of 90o
- θ with the x-axis. Let x = 0, y
= 0, t = 0 be the coordinates of the ball at the instant the ball makes contact
with the inclined plane the first time.
In the time interval between the first and second bounce
the equations giving the position and velocity of the ball as a function of time
are:
x(t) = v sinθ t +
½ g sinθ t2, y(t) = v cosθ
t - ½ g cosθ t2
vx(t) = v sinθ
+ g sinθ t, vy(t) = v cosθ
- g cosθ t
The ball bounces for the second time when y(t) = 0, t = ta
= 2v/g.
x(ta) = (2v2/g) sinθ
+ (2v2/g) sinθ = (4v2/g)
sinθ
vx(ta) = v sinθ + 2v sinθ = 3v sinθ,
vy(ta) = v cosθ -
2v cosθ = -v cosθ
Just after the second bounce, the velocity of the ball is vx
= 3v sinθ, vy = v cosθ.
Let t' = t - ta. Between the second and the
third bounce the equations giving the position and velocity of the ball as a
function of time are:
x(t) - x(ta) = 3v sinθ t' + ½ g sinθ t'2,
y(t) = v cosθ t' - ½ g cosθ
t'2
The ball bounces for the third time when y(t) = 0, t' = tb
= 2v/g.
x(ta + tb) - x(ta) = (6v2/g)sinθ
+ (2v2/g) sinθ = (8v2/g)
sinθ
Therefore d12/d23
= x(ta)/( x(ta + tb) - x(ta)) = ½.
Problem:
Three elastic spheres of equal size are suspended on light strings
as shown; the spheres nearly touch each other. The mass M of the
middle sphere is unknown; the masses of the other two spheres are 4m
and m. The sphere of mass 4m is pulled sideways until it is elevated
a distance h from its equilibrium position and then released. What must
the mass of the middle sphere be in order for the sphere of mass m to rise to a
maximum possible elevation after the first collision with the middle
sphere? What is that maximum elevation H?
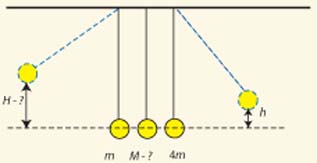
Solution:
- Concepts:
Elastic collisions, energy and momentum conservation
- Reasoning:
In elastic collisions mechanical energy and momentum are
conserved.
- Details of the calculation:
For a collision between a sphere of mass
m1 and initial velocity v1i and a stationary sphere of
mass m2, energy and momentum conservation yield v2f =
2m1v1i/(m1 + m2).
Let mass 4m
move with speed v = (2gh)1/2 just before the first collision.
Here we have for the collision between 4m and M: v2f = 8mv/(4m +
M).
Now v2f becomes v1i for the collision between M
and m.
We have for this collision: vf = 16mMv/[(m + M)(4m +
M)], where vf is the speed of mass m immediately after the
collision.
We want to maximize vf with respect to M.
vf
= 16mMv/(M2 + 5Mm + 4m2),
dvf/dM = 0
--> 16m(M2 + 5Mm + 4m2) - 16mM(2M + 5m) = 0.
16M2
= 64m2, M = 2m.
This is the only physical value for M for
which dvf/dM = 0.
vf --> 0 as M --> 0 or infinity,
we have a maximum.
vfmax = (16/9)v = (16/9)(2gh)1/2.
H = vfmax2/2g = (16/9)2h = 3.16 h.





