Variable mass

"Variable mass" problems

Problem:

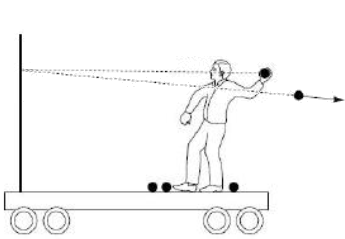
A 60 kg man standing fixed to the ground, can throw a m = 150 g baseball horizontally with a maximum speed of v₀ = 25 m/s.
(a) How much mechanical energy does he put into the throw?
(b) Assume the man stands fixed to a 9.25 kg platform which moves frictionless with respect to the ground. He has five 150 g baseballs and throws one of the baseballs horizontally as shown, putting in the same amount of mechanical energy as found in part (a). The collision of the ball with the platform wall is elastic. What is his velocity (magnitude and direction) after the throw?

(c) What is the horizontal velocity component of the ball relative to the man?
(d) Assume the man throws the remaining four balls sequentially, always putting in the same amount of mechanical energy. What will be his final velocity?

Solution

Concepts:
Energy and momentum conservation
Reasoning:
If the man is fixed to the ground, the mechanical energy is equal to the kinetic energy of the baseball. If he is fixed to the platform, the mechanical energy is shared between the ball and the recoiling system.
Since the collision of the ball with the platform wall is elastic, the final velocities are the same as those for a system where the ball is thrown in the opposite direction.
Details of the calculation:
(a) E = ½mv₀² = 46.875 J.
(b) E = ½MV² + ½mv², energy conservation.
MV = -mv, momentum conservation.
Here m is the mass of the baseball, M is the mass of the recoiling system, v is the velocity of the baseball (chose the coordinate system so v points in the positive x-direction) and V is the velocity of M.
(1D motion, the signs of v and V carry the directional information.)
v = -MV/m, E = ½MV² + ½M²V²/m. V² = 2Em/(M(M + m)).
V = -(2Em/(M(M + m)))^½, the man is moving in the negative x-direction.
Let M₀ be the mass of the man and the platform and the 5 balls, M₀ = 70 kg. M = M₀ - m.
V² = 2*(46.875 J)*0.15/(69.85*70) (m/s)², V = -5.36 cm/s.

(c) v - V = (M/m + 1) (2Em/(M(M + m)))^½ = (2E(M + m)/(Mm)))^½ = 25.02 m/s is the relative velocity of the ball with respect to the man.

(d) Before the nth throw, the platform with the man and the remaining balls is an inertial frame with mass M₀ - (n - 1)m. After the nth throw M_n' = M₀ - nm is the mass of the recoiling system.
The velocity of the recoiling system in this inertial frame is V' = -(2Em/(M_n'(M_n'+ m)))^½.
After 5 balls have been thrown, the velocity of the man with respect to the ground is
V_f = -(2Em)^½∑_n=1⁵(M_n'(M_n'+ m))^-½.
M_n'(M_n'+ m) ≈ M₀² - 2M₀nm + M₀m = M₀²(1 - (2n - 1)m/M₀).
(M_n'(M_n'+ m))^-½ ≈ M₀^-1(1 + (n - ½)m/M₀).
V_f = -(2Em/M₀²)^½∑_n=1⁵(1 + (n - ½)m/M₀)
= -(2Em/M₀²)^½[5*(1 - ½m/M₀) + (m/M₀)∑_n=1⁵n]
= -(2Em/M₀²)^½[5*(1 - ½m/M₀) + (m/M₀)*15] = -26.92 cm/s.

Problem:

A trainload of empty, non-leaking coal cars is accelerating in an easterly direction due to a constant force F. It starts to rain, and the rain has a velocity which has a horizontal component v₀, in a westerly direction. The rain fills the cars at a constant rate of λ mass units per unit time. Under these conditions the train will reach a maximum velocity.
(a) Find the maximum velocity and express it in terms of F, v₀, and λ.
(b) Find the train's velocity v(t).

Solution:

Concepts:
Newton's 2nd law, F = dp/dt, dp = p(t + dt) - p(t)
Reasoning:
Assume the train moves into the x-direction. Its mass is m(t) = m₀ + λt.
In a small time interval Δt its momentum changes by Δp = P_after - P_before = mΔv + Δm(v + v₀)
dp = mdv + dmv + dmv₀.
Details of the calculation:
(a) F = mdv/dt + (dm/dt)(v + v₀) = (m₀ + λt)dv/dt + λ(v + v₀).
dv/dt = F/(m₀ + λt) - λ(v + v₀)/(m₀ + λt).
When v = v_max, dv/dt = 0. Then F = λ(v + v₀), v_max = F/λ - v₀.
(b) Let t' = m₀ + λt. dv/dt = λdv/dt'. dv/dt' = (F/λ - (v + v₀))/t'.
Let V = F/λ - (v + v₀), then dV = -dv.
dV/dt' = -V/t'. dV/V = -dt'/t'. V(t') = B/t'. B is a constant which depends on the initial conditions.
F/λ - v(t) - v₀ = B/(m₀ + λt). v(t) = F/λ - v₀ - B/(m₀ + λt).

Problem:

Water starts emerging horizontally with speed v₀ from a nozzle and just reaches the far end of a box with mass m₀ and length l which rests on a frictionless surface.
The mass flow rate of the water is λ.

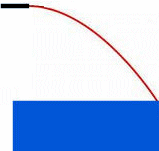
Find the velocity of the box as a function of time as long as water pours into the box.

Solution:

Concepts:
Newton's 2nd law, F = dp/dt, dp = p(t + dt) - p(t)
Reasoning:
F = 0, dp = m dv + dm v - dm v₀.
Details of the calculation:
dp/dt = (dm/dt)(v - v₀) + m dv/dt = λ(v - v₀) + (m₀ + λt)dv/dt = 0.
dv/dt = -λ(v - v₀)/(m₀ + λt).
Let t' = m₀ + λt, v' = v - v₀, then dv'/dt' = -v'/t'. v' = B/t'.
v = v₀ + B/(m₀ + λt), v(0) = 0 --> B = -m₀v₀.
v(t) = v₀ - m₀v₀/(m₀ + λt) = λt₀v₀/(m₀ + λt).

Problem:

A spherical water droplet falls without friction under the influence of gravity through an atmosphere saturated with water vapor. Let its initial radius at t = 0 be C, its initial velocity v₀. As a result of condensation, the water drop experiences a continuous increase in mass, proportional to its surface. Its radius R then increases linearly with time. Integrate the differential equation of the motion by introducing R instead of t as independent variable. Show that for C = 0 the velocity increases linearly with time.

Solution:

Concepts:
Newton's 2^nd law: F = dp/dt, dp = mdv + vdm
Reasoning:
The system consists of the moisture, with zero momentum. and the water droplet with momentum p. In a time interval dt a small amount dm of the moisture receives an impulse vdm. In the same time interval the velocity of the drop changes by dv. The total momentum change of the system is dp = mdv + vdm.
Details of the calculation:
Choose a coordinate system such that the z-axis points downward and F = mgk. The problem then is a one-dimensional problem.
p = mv, dp/dt = mdv/dt + vdm/dt = mg. dv/dt = g - (v/m)dm/dt.
m = ρ4πR³/3, dm/dt = λ4πR², since the increase in mass per unit time is proportional to the surface area.
But we also have dm/dt = ρ4πR²dR/dt. Therefore dR/dt = λ/ρ, R = C + (λ/ρ)t.
dv/dt = (dv/dR)(dR/dt) = (λ/ρ)(dv/dR).
But we also have
dv/dt = g - (v/m)(dm/dt) = g - 3vλ/(ρR).
Therefore
dv/dR = (ρg/λ) - 3v/R.
[The differential equation dx/dt + nx/t = B has the general solution
x = At^-n + Bt/(n+1).]
v = AR^-3 + (ρg/4λ)R, v = A/(C + (λ/ρ)t)³ + (ρg/(4λ))(C + (λ/ρ)t).
At t = 0 v = v₀. v₀ = A/C³ + ρgC/(4λ), A = v₀C³- ρgC⁴/(4λ).
As C goes to zero A goes to zero, and v = (ρg/(4λ))(λ/ρ)t = gt/4.
v increases linearly with time.

Problem:

A spacecraft of mass m₀ and cross-sectional area A is coasting with velocity v₀ when at t = 0 it encounters a stationary dust cloud of density ρ. If the dust sticks to the spacecraft, solve for the speed of the spacecraft as a function of time. Assume A is constant over time.

Solution:

Concepts:
Newton's 2^nd law: F = dp/dt, dp = mdv + vdm
Reasoning:
The system consists of the dust, with zero momentum and the spacecraft with momentum p. In a time interval dt a small amount dm of the dust receives an impulse vdm. In the same time interval the velocity of the spacecraft changes by dv. The total momentum change of the system is dp = mdv + vdm = 0.
Details of the calculation:
p = mv, dp/dt = mdv/dt + vdm/dt = 0. dv/dt = -(v/m)dm/dt.
dm/dt = ρAv since the increase in mass per unit time is proportional to A.
mv = m₀v₀ since p is constant.
dv/dt = -(v/m)ρAv. dv/v³ = -ρAdt/(mv) = -ρAdt/(m₀v₀).
Integrating we obtain 1/v² = 2ρAt/(m₀v₀) + C, with C = 1/v₀², since at t = 0 v = v₀.
v(t) = [1/v₀² + 2ρAt/(m₀v₀)]^-½ = [m₀v₀²/( m₀ + 2ρAtv₀)]^½.

Problem:

The UT Physics Department's vacuum cannon fires a 3.8 cm diameter, 2.3 g ping pong ball through a 1.8 m long pipe that has been evacuated to a pressure which is a very small fraction of atmospheric pressure, so that its initial acceleration is simply determined by Newton's second law and the force produced by one atmosphere of pressure acting on the cross-sectional area of the ping pong ball. (The ends of the pipe are sealed with a very thin plastic film.) However, as the ball accelerates down the pipe, the atmospheric pressure-force also has to accelerate the mass of air that rushes in to fill the pipe behind the ball. Assume that this variable mass piston of air is a cylinder having the same density as the surrounding atmosphere (1.3 kg/m³) and an initial mass of zero, and that none of this air leaks around the edges of the ball into the evacuated space ahead of the ball.
(a) Neglecting the effect of the variable mass piston of air, i.e. assuming the acceleration to be constant along the length of the pipe and equal to the initial acceleration, constant acceleration, find the (incorrectly predicted) exit velocity of the ball.
(b) Derive an expression for the speed of the ball as a function of distance accelerated down the cannon, taking the variable mass piston of air into account.
(c) Evaluate the terminal velocity (for a very long cannon) for the numerical values given above, and the predicted velocity for our version of the cannon, which is 1.8 m long. Compare these values, and the result of (a), with the speed of sound in air at room temperature (about 340 m/s) and discuss that comparison.

Solution:

Concepts:
Newton's 2nd law, F = dp/dt
Reasoning:
Newton's 2nd law, F = dp/dt, yields the equations of motion, which can be solved for the velocity as a function of position.
Details of the calculation:
(a) P = F/A = 101 kPa. F = P*πr² = 114.5 N.
a = F/m = 4.98*10⁴ m/s². v(d = 1.8 m) = (2a*1.8 m)^½ = 423 m/s.
(b) F = PA = dp/dt
p = mv = (m_ball + m_air)v,   dp = vdm_air + mdv,   dm_air = ρAdx, m = m_ball + ρAx.
PA = ρAv² + (m_ball + ρAx)dv/dt.
dv/dt = (dv/dx)v,   vdv/dx = (PA - ρAv²)/ (m_ball + ρAx).
Let x' = (m_ball + ρAx), then dx' = ρAdx.
vdv/dx' = (PA/(ρA) - v²)/x',   vdv/dx' = (B - v²)/x', dv²/dx' = 2B/x' - 2v²/x'.
Let v'² = B - v². Then dv'²/dx' = -2v'²/x'. This integrates to
v'² = C₁/x'², v² = P/ρ - C₁/x'².
The initial conditions are v² = 0 and x' = m_ball.
Therefore C₁ = m_ball² P/ρ,
v²(x) = (P/ρ)(1 - m_ball²/(m_ball + ρAx)²).
(c) As x --> infinity, v² --> P/ρ = (1.01*10⁵ N/m²)/(1.3 kg/m³),   v --> 279 m/s.
v(1.8 m) = 279 m/s (1 - (2.3*10^-3/(2.3*10^-3 + 1.3*p*(1.9*10^-2)²*1.8)²)^½= 247 m/s.
The terminal velocity of 279 m/s and the calculated velocity of 247 m/s are below the speed of sound and hence are reasonable, but the result of 423 m/s for part a is greater than the speed of sound and hence is not physically reasonable. However, when v approaches the speed of sound, the air can no longer be treated as incompressible, and hence the results of part c are also incorrect. For incompressible flow we need v/v_sound < 0.3. Moreover, the assumption of plug-like flow will also become invalid.