Equilibrium

Problem:

A 1500 kg automobile has a wheelbase (the distance between the axles) of 3 m.  The center of mass of the automobile is on the centerline at a point 1.2 m behind the front axle.  Find the force exerted by the ground on each wheel.

Solution:

• Concepts:
  Static equilibrium
• Reasoning:
  The car is in static equilibrium, F_tot = 0, τ_tot = 0.  The force of gravity Mg acts on the center of mass of the object.  It produces no torque about the CM.
• Details of the calculation:
  
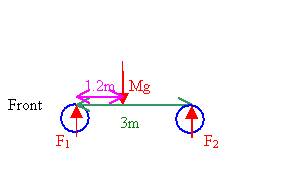
  F_tot = F₁ + F₂ - Mg = 0.
  τ_tot = F₂ 1.8 m - F₁ 1.2 m = 0.
  F₁ = 1.5 F₂.
  2.5F₂ = Mg = 14700 N, F₂ = 5880 N. F₁ = 8820 N.
  The force exerted by the ground on each rear wheel is F₂/2 = 2940 N and the force exerted by the ground on each front wheel is F_½ = 4410 N.

Problem:

A board weighing 90 N and 12 m long rests on two supports with each support being one meter from its respective ends.  A 360 N block is placed on the board 2 m from the rightmost support. Find the force that is exerted by each support on the board.

Solution:

• Concepts:
  Equilibrium
• Reasoning:
  Equilibrium implies no net force and no net torque.
• Details of the calculation:
  No net force:
  F_left + F_right - m_board*g - m_load*g = 0.
  F_left + F_right = (90 + 360) N = 450 N.
  No net torque about any point:
  Choose the left support point.  F_right*10 m - m_board*g*5 m - m_load*g*8 m = 0.
  F_right = (90*5 + 360*8)/10 N = 333 N.
  F_left = 117 N.
  Both F_left and F_right point upward.

Problem:

A uniform massive rod AB of length L rests at the inclination ±10^o with respect to the horizontal with end A in contact with a vertical wall.  The two configurations are shown in figures a and b.  End of the rod is supported by a massless cord BC, which is of length 1.2 L and is attached at C, a point on the wall above A.  What coefficient of static friction between A and the wall is necessary to achieve each configuration?

Solution:

• Concepts:
  Static equilibrium, static friction: F_max = μN, N = normal force
• Reasoning:
  In static equilibrium the total force and the total torque about the CM must be zero.  F = 0, τ = 0
  
  The diagram shows the forces on the rod.  The forces acting at the ends of the rod can exert a torque about the CM.
• Details of the calculation:
  (i) F_y = Tsinφ + F_f - mg = 0
  (ii) F_x = -Tcosφ + F_R = 0
  (iii) τ = (L/2)[Tsin(φ - θ) - F_f cosθ - F_R sinθ] = 0
  Note:  F_f could be positive or negative.
  We have 3 equations and 3 unknowns. We are, however, only interested in the ratio F_f/F_R.
  Inserting (ii) into (iii) we have
  T sin(φ - θ) - F_f cosθ - T cosφ sinθ = 0,  F_f = [T sin(φ - θ) - T cosφ sinθ]/cosθ.
  μ = |F_f|/N = |F_f|/F_R = F_f/(Tcosφ) = [sin(φ - θ) - cosφ sinθ]/[cosφ cosθ].
  cosφ = L cos10^o/(1.2 L) = 0.82067.
  φ = 34.848^o.
  case (a): θ = 10^o,  μ = 0.3436 or greater.
  case (b): θ = -10^o,  μ = 1.0489 or greater.

Problem:

A homogeneous ladder of length L leans against a wall (see figure).  The coefficient of friction with the ground is μ₁, the coefficient of friction with the wall is μ₂.  Find the minimal angle θ, below which the ladder will slip.

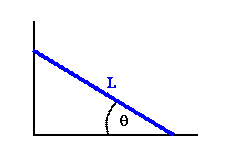
Solution:

• Concepts:
  Static equilibrium, static friction: F_max = μN, N = normal force
• Reasoning:
  In static equilibrium the total force and the total torque about the CM must be zero.  F = 0, τ = 0
• Details aof the calculations:
  
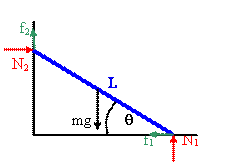
  In equilibrium:
  F_y = 0:  N₁ + f₂ = mg   (1)
  F_x = 0:  N₂ = f₁  (2)
  The torque about the CM is zero:  N₂sinθ + f₂cosθ + f₁sinθ = N₁cosθ   (3)
  (N₂ + f₁)sinθ = (N₁ - f₂)cosθ   (rewriting (3))
  2f₁sinθ = (mg - 2f₂)cosθ   (eliminating N₁ and N₂ from (3) using (1) and (2))
  tanθ = (mg - 2f₂)/(2f₁)
  The angle θ is smallest when both f₁ and f₂ have their maximum value.
  tanθ = (mg- 2μ₂N₂)/(2μ₁N₁) = (N₁ + μ₂μ₁N₁- 2μ₁μ₂N₁)/(2μ₁N₁) = (1 - μ₂μ₁)/(2μ₁).
  For smaller angles the ladder will slip.

Problem:

A 5.0 m long ladder leans against a wall at a point 4.0 m above the ground.  The ladder is uniform and has a mass of 12.0 kg.  Assume the wall is frictionless, but the ground is not.
(a)  Determine the forces exerted on the ladder by the ground and the wall.
(b)  If the coefficient of static friction between the ladder and the ground is 0.40, how far up the ladder can a 58 kg person climb before the ladder slips?

Solution:

• Concepts:
  Static equilibrium:  F = 0, τ = 0
• Reasoning:
  In static equilibrium the total force and the total torque about the CM must be zero.
• Details of the calculation:
  
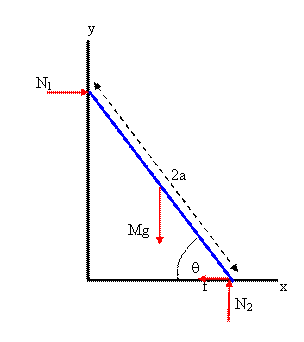
  (a)  F_x = N₁ - f = 0.  F_y = N₂ - Mg = 0.  τ = N₂ a cosθ  - f a sinθ - N₁ a sinθ = 0. (about CM)
  Mg 3/5 - f  4/5 - f 4/5 = 0.  3 Mg - 8 f = 0,  f = (3/8) Mg = 44.1 N.
  The force exerted by the ground on the ladder is 117.6 N j - 44.1 N i, and the force exerted on the ladder by the wall is 44.1 N i.
  (b)  With a person of mass m a distance on the ladder at a distance a + d from the end on the ground we have
  F_x = N₁ - f = 0.  F_y = N₂ - Mg - mg = 0. 
  τ = N₂ a cosθ  + mg d cosθ - f a sinθ - N₁ a sinθ = 0.
  3(M + m)g + 3mg(d/a) - 8f = 0.  f = 3g(M + m (1 + (d/a))/8.
  μ = f/N₂ = 3(M + m (1 + (d/a))/[8(M + m)].
  d/a = (8μ/3 - 1)(M + m)/m = 0.08.
  d + a = 2.7 m.

Problem:

A long thin uniform rod lies flat on the table as shown.  One end of the rod is slowly (quasi-statically) pulled up by a force that remains perpendicular to the rod at all times.  What minimum coefficient of static friction is required so that the rod can be brought to the vertical position without any slipping of the bottom end?

Solution:

• Concepts:
  Static equilibrium
• Reasoning:
  Since the rod is raised slowly (quasi-statically), the entire system remains in equilibrium at any moment in time. Thus, the torque about the point of rotation of the rod is zero, and the net external force is 0.
• Details of the calculation:
  
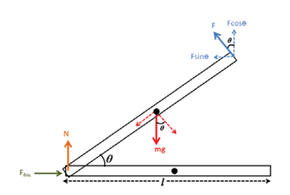
  Assume that 0 < θ < π/2.
  F_fri = Fsinθ, τ = -Fl + mglcosθ/2 = 0  -->  F = mgcosθ/2,  N = mg - Fcosθ.
  We need  the coefficient of friction μ > Fsinθ /( mg - Fcosθ).
  Eliminating F from the equation we have μ > sinθ cosθ/(2 - cos²θ).
  Find the maximum μ as a function of angle from dμ/dθ = 0.
  dμ/dθ = [(2 - cos²θ)(2cos²θ - 1) - 2cos²θ (1 - cos²θ)]/(2 - cos²θ)² = 0
  Since the denominator is finite the numerator has to be zero.  Let x = cos²θ.
  (2 - x)(2x - 1) - 2x(1 - x) = 0, x = (2/3),  cosθ = (2/3)^½, sinθ = (1/3)^½.
  The coefficient of friction must be large enough to prevent slipping at that angle.
  μ > (1/3)^½(2/3)^½/(2  - (2/3)) = (1/8)^½.  μ_min = (1/8)^½.

Problem:

Two steel balls, each of radius R and mass M, are packed into a bottomless cylindrical thin-walled tube of diameter R(2 + √2).  The tube and balls sit on a table.  There is no friction anywhere in the problem.  Find the minimum mass of the tube m that will keep the system in equilibrium.

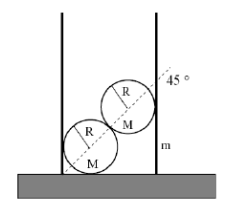
Solution:

• Concepts:
  Static equilibrium
• Reasoning:
  For the system to be in equilibrium the net force on and the net torque on all components must be zero.
• Details of the calculation:
  
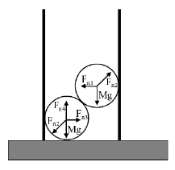
  Consider the top ball.  We need
  Mg = F_n2/√2 and F_n1 = F_n2/√2.  Therefore F_n1 = Mg, F_n2 = Mg/√2.
  Consider the bottom ball.  We need
  F_n3 = F_n2/√2 and Mg + F_n2/√2 = F_n4. 
  Therefore F_n3 = Mg, F_n4 = 2Mg.
  
  No torque is exerted on the balls. 
  The net force on the tube is zero.
  
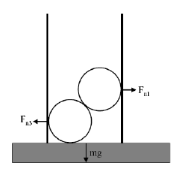
  Let us calculate the net torque on the tube about the right lower edge in the diagram.  In equilibrium we need this torque to be zero.
  The balls, pushing against the wall, and the weight of the cylinder exert a torque about the right lower edge.
  If the net torque due to these forces points out of the page, then the reaction force from the ground on the left lower edge will cancel it, since the cylinder cannot move into the ground.
  For a cylinder with minimum mass m the torque due to the reaction force from the ground is zero.
  0 = F_n1 R(2 + √2) - F_n3R - mg R(2 + √2)/2.
  Substituting we obtain
  0 = M(1 + √2) - M - mg(1 + 1/√2), which yields the minimum mass of the tube,
  m = 2M/(1 + √2).

Problem:

A uniform metal plate has mass m and length 4R.  The plate is bent in half at right angles and placed on a horizontal cylinder of radius R as shown.  

The top half of the plate is horizontal.  The cylinder is fixed.  What is the minimum coefficient of static friction μ_s between the plate and the cylinder that allows the plate to remain at rest?

Solution:

• Concepts:
  Equilibrium, free-body diagrams
• Reasoning:
  Draw a free-body diagram that shows all the forces that can act on the plate.   In equilibrium the net force and the net torque about any point have to be zero.
• Details of the calculation:
  
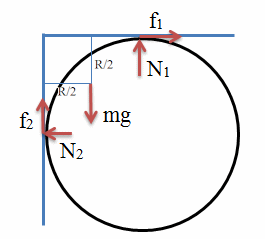
  Force:
  horizontal component:  f₁ = N₂
  vertical component:  f₂ + N₁ = mg
  We also have f₁ ≤ μ_sN₁,  f₂ ≤ μ_sN₂.
  torque about the corner:
  mg*R/2 + N₂*R = N₁*R
  Combining these equations we eliminate f₂.
  f₁ + f₂ = mg/2,  f₂ ≤ μ_sf₁, 
  N₁ = f₁ + mg/2,  f₁ ≤ μ_s(f₁ + mg/2),  f₁ ≤ μ_s(mg/2)/(1 - μ_s).
  But mg/2 ≤ f1 + μ_sf₁, so 1 ≤  μ_s(1 + μ_s)/(1 - μ_s),  μ_s² + 2μ_s - 1 ≥ 0.
  The minimum μ_s satisfies μ_s² + 2μ_s - 1 = 0.  μ_s(min) = 2^½ - 1.

Problem:

A rope is wound around a cylinder of radius R with a contact angle φ (φ can be larger than 2π) to hold a massive object in place, for example to secure a ship for docking.  The object exerts a force F on one end of the rope and the other end of the rope held by a force T.   The coefficient of static friction between the rope and the cylinder is k.  Find the ratio F/T required to keep the object stationary as a function of φ.

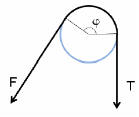
Solution:

• Concepts:
  Equilibrium, friction
• Reasoning:
  The frictional force is proportional to the normal force.  We have to find the normal force a small section of rope exerts on the cylinder.
• Details of the calculation:
  Consider an infinitesimally small section of rope of length Rdθ, acted on by the forces T'' = T' + dT' and T' as shown. 
  
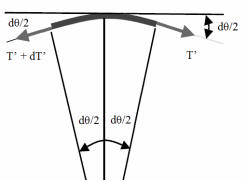
  The magnitudes of the tangential and normal components of these forces are
  T'_t = T'cos(dθ/2), T'_n = T'sin(dθ/2), T''_t = T''cos(dθ/2), T''_n = T''sin(dθ/2).
  The magnitude of the net tangential force is T''_t - T'_t = dT'cos(dθ/2) = dT'.
  The magnitude of the net normal force is N = (2T' + dT')sin(dθ/2) = T'dθ since dθ is infinitesimal and we only keep first order terms in the small quantities.
  For the section of rope to be in equilibrium, we need |dT'| ≤ kN = kT'dθ
  |dT'|/T' ≤ kdθ.
  Assume we want to find the minimum value of T.  (T < F, dT' is positive.)
  Integrating from θ = 0 to θ = φ we find ln (F/T) = -kφ,  F/T = exp(-kφ).
  To keep the object stationary we need F/T = exp(kφ), T = Fexp(-kφ).
  (Here we assume that φ is small enough so that friction alone does not keep the object stationary.)

Problem:

A rope rests on two platforms which are both inclined at angle θ (which you are free to pick) as shown.  The rope has uniform density and its coefficient of friction with the platform is 1.  The system has left-right symmetry.  What is the largest possible fraction of the rope that does not touch the platform?  What angle θ allows this maximum value?

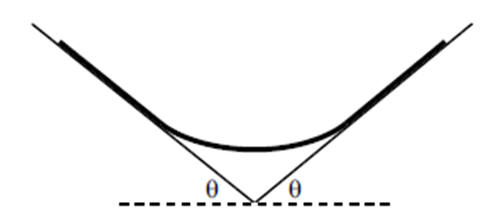
Solution:

• Concepts:
  Static equilibrium
• Reasoning:
  Let the total mass of the rope be m and let a fraction f of it hang in the air.  For each half of the symmetrical situation, the weight of the hanging fraction must be balanced by the vertical component of the tension in the rope.  For the fraction of the rope touching the platform the frictional force must balance the gravitational force component along the plane plus the tension in the lower end.
  For a given angle θ:  
  maximum frictional force --> maximum tension --> maximum hanging fraction
• Details of the calculation:
  For the right half:
  Hanging weight = (f/2)mg.  Vertical component of tension = T sinθ. 
  (f/2)mg = T sinθ.  T = (f/2)mg/sinθ.
  Mass of rope touching platform = (1 - f)m/2.  Normal force = (1 - f)(m/2)g cosθ.
  Maximum frictional force = (1 - f)(m/2)g cosθ, since the coefficient of friction is 1.
  Gravitational force component along the plane = (1 - f)(m/2)g sinθ.
  (1 - f)(m/2)g cosθ = (1 - f)(m/2)g sinθ + (f/2)mg/sinθ.
  f = (cosθ sinθ - sin²θ)/(1 + cosθ sinθ - sin²θ).  This can also be written as
  f = (sin2θ + cos2θ - 1)/(2 + sin2θ + cos2θ - 1).
  To find the angle for which f_max(θ) = f_max, set df/dθ = 0.
  θ_max = 22.5^o.  f_max = (2^1/2 - 1)/(2^1/2 + 1) = 0.172.

Problem:

A floor has an area of 100 m².  Its consists of two very stiff plates, separated by coil springs to give it some "bounce".  The equilibrium separation is 5 cm.  There are 100 evenly spaced identical springs per square meter.  The spring constant of each spring is k = 10³ N/m.
(a)  Find the Young's modulus of this floor.
(b)  When 20 people with a combine mass of 1200 kg rest on this floor (in equilibrium), by how much does the distance between the plates change?
(c)  In (b), what is the elastic (strain) energy stored in the floor?

Solution:

• Concepts:
  Young's modulus
• Reasoning:
  The Young's modulus is defined through F/A = Y ΔL/L,
  Y = (tensile stress)/(tensile strain).
• Details of the calculation:
  (a)  The effective spring constant of the system of 10⁴ springs in parallel is 10⁷ N/m.
  Hooke's law:   F/ΔL = k = YA/L = 10⁷ N/m.
  Y = (10⁷ N/m)*(5*10^-2 m)/100 m² = 5*10³ N/m².
  (b)  ΔL = FL/(AY) = (1200 kg)*(9.8 m/s²)*(5*10^-2 m)/(100 m² * 5*10³ N/m²) = 1.18 mm.
  The distance between the plates change by 1.18 mm.
  (c)  We model the floor as a compressed spring.  The spring constant k = 10⁷ N/m.
  The elastic energy stored in the floor is ½k ΔL² = 7 J.
  Think about:  Why not mgΔL?