Shear stress and strain, shear modulus
Shear modulus S = (shear stress)/(shear strain) = (F||/A)/(Δx/L0)
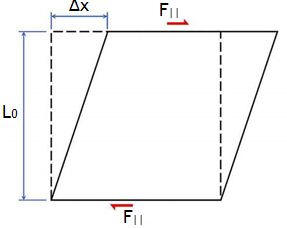
Shear stress: 0.245 N/(6*10-2 m)2 = 68 Pa.
Shear strain = (5 mm)/(20 mm) = ¼.
Shear modulus S = 272 Pa.
A floor has an area of 100 m2. Its consists of two very stiff
plates, separated by coil springs to give it some "bounce". The
equilibrium separation is 5 cm. There are 100 evenly spaced identical
springs per square meter. The spring constant of each spring is k = 103
N/m.
(a) Find the Young's modulus of this floor.
(b) When 20 people with a combine mass of 1200 kg rest on this floor (in
equilibrium), by
how much does the distance between the plates change?
(c) In (b), what is the elastic (strain) energy stored in the floor?
Solution:
A block of gelatin has dimensions 60 mm by 60 mm by 20 mm when unstressed. It rests on one of the 60 mm by 60 mm sides. A force of 0.245 N is applied tangentially to the upper surface causing a 5 mm displacement relative to the lower surface. Find the shear stress, the shear strain, and shear modulus.
Solutions

Two rigid parallel plates are connected by a composite material consisting of parallel fibers in a plastic matrix as shown in the figure.
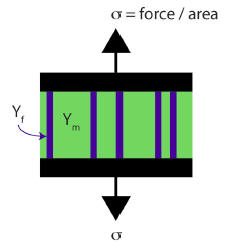
The volume fraction of the fibers relative to the total volume of the
composite is f. A stress σ is applied to the plates. The Young's
modulus of the fiber is Yf, and that of the matrix is Ym. Assuming there is no
delamination across the fiber/matrix interface, the strains ε in the components
of the composite are equal (isostrain).
(a) Write Hooke's law in terms of σ, Y and strain, ε.
(b) Write the expression of the condition of isostrain in terms of
σ, Y, ε for the fiber and matrix.
(c) Derive an expression for the Young's modulus, Yeff, of the
composite.
Solution: