Work and conservation of energy

Work

Problem:

A cyclist intends to cycle up a 8^o hill whose vertical height is 150 m with constant speed.  If each complete revolution of the pedals moves the bike 6 m along its path, calculate the average force that must be exerted on the pedals tangent to their circular path.  Neglect work done by friction and other losses.  The pedals turn in a circle of diameter 30 cm.  The total mass of the cyclist and his bike is 100 kg.

Solution:

• Concepts:
  Work and energy
• Reasoning:
  The work done by the cyclist changes the potential energy of the system.
• Details of the calculation:
  The net work done by the cyclist is during one revolution of the pedals is
  W = mg∆h = 100*9.8*6*sin(8^o) J = 818 J.
  During one one revolution the pedal travels a distance s.
  W = <F>*s = <F>*2π(0.15 m) = (0.942 m)*<F>
  <F> = (818 J)/( (0.942 m) = 868 N

Conservation of energy

Problem:

A pencil of length L is held vertically with its point on a desk and then allowed to fall over.  Assuming that the point does not slip, find the speed of the eraser just as it strikes the desk.  Compare this with the speed that would result from free fall from a height equal to the length of the pencil.

Solution:

• Concepts:
  Energy conservation
• Reasoning:
  Gravity is a conservative force.  We have pure rotation about a point.
• Details of the calculation:
  ½Iω² = mgL/2.  I = mL²/3.
  ω² = 3g/L.  v_tip = ωL = (3gL)^½.
  Speed of eraser that falls freely from a height L: v = (2gL)^½.
  [½mv² = mgL]

Problem:

Two thin beams of mass m and length l are connected by a frictionless hinge and thread.

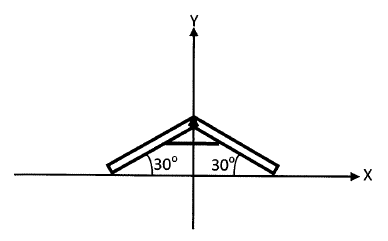
The system rests on a smooth surface.  At t = 0 the thread is cut.  Neglect the mass of the hinge and the treat.
(a)  Find the speed of the hinge when it hits the floor.
(b)  Find the time it takes for the hinge to hit the floor in terms of an integral.

Solution:

• Concepts:
  Energy conservation
• Reasoning:
  The system is frictionless.  The symmetry of the problem tells us that the hinge will fall vertically.   The potential energy of the two beams will be converted into translational kinetic energy of their CMs and rotational kinetic energy about their CMs.
• Details of the calculation:
  (a)  For a given angle θ, the CMs of beams 1 and 2 are at positions
  x₁ = ½lcosθ, y₁ = ½lsinθ, x₂ = -½lcosθ, y₂ = ½lsinθ.
  Their velocity components are
  dx₁/dt = -½lsinθdθ/dt, dy₁/dt = ½lcosθdθ/dt, dx₂/dt = ½lsinθdθ/dt, dy₂/dt = ½lcosθdθ/dt.
  The speed of the CM of each rod is v = [¼l²(dθ/dt)²]^½ = ½l|dθ/dt|
  and its angular speed about its CM is is |dθ/dt| = ω = 2v/l.
  The speed of the hinge is v_h = 2v.
  The moment of inertia if each rod about its CM is I = ml²/12.
  The kinetic energy of the system is 2[½mv² + ½Iω²]
  = ¼ml²(dθ/dt)² + (1/12)ml²(dθ/dt)² =  (1/3)ml²(dθ/dt)².
  The potential energy of the system is mglsinθ.
  
  Energy conservation:  (1/3)ml²(dθ/dt)² + mglsinθ = mglsin(30^o) = ½mgl.
  (dθ/dt)² =  (3g/l)(0.5 - sinθ).
  When θ = 0 the |dθ/dt| = (3g/(2l))^½, v_h = l|dθ/dt| = (3lg/2))^½.
  This is the speed with which the hinge hits the floor.
  
  (b)  dt = dθ/[dθ/dt], t = -∫_{30 deg}⁰ dθ/[(3g/2l)(1 - 2sinθ)]^½ = (2l/3g)^½∫₀^{30 deg} dθ/(1 - 2sinθ)^½.

Problem:

Galileo wants to demonstrate that unequal masses fall with a uniform acceleration by dropping two spherically symmetric masses simultaneously from the same height z.  Ideally we know that they should hit the ground at the same time, t = (2z/g)^½,  where g is the acceleration due to gravity.
Unfortunately for Galileo, the surface of the first sphere is slightly irregular, so the otherwise negligible air drag induces a rotation with an angular frequency proportional to the velocity, ω = εv₁.  The second sphere does not rotate.  Assume that ε is constant and ignore possible heating of the air by friction.
Find the ratio of impact times t₁/t₂ of the two spheres.  The answer should involve only the coefficient ε and the mass m₁ and moment of inertia I₁ of the first sphere.

Solution:

• Concepts:
  Energy conservation
• Reasoning:
  Gravitational potential energy is converted into kinetic energy.  The rotating sphere has translational as well as rotational kinetic energy.
• Details of the calculation:
  For the non-rotating sphere we have as a function of the distance z' below the point of release
  mgz' = ½mv²,  v²(z') = 2gz'.  This yields t(z') = (2z'/g)^½.
  For the rotating sphere we have as a function of the distance z' below the point of release
  m₁gz' = ½m₁v₁² + ½I₁ω² = ½m₁v₁² + ½I₁ε²v₁² = ½(m₁ + ε²I₁)v₁²,
  v₁² = 2g[m₁/(m₁ + ε²I₁)]z'.
  This yields t₁(z') = (2z'/g')^½, with g' = g[m₁/(m₁ + ε²I₁)].
  Therefore t₁/t₂ = (g/g')^½ = [(m₁ + ε²I₁)/m₁)]^½.

Problem:

Find the fraction of the kinetic energy that is translational and rotational when
(a)  a hoop
(b)  a disc and
(c)  a sphere rolls down an inclined plane of height h.  Find the velocity at the bottom in each case.  Compare with a block sliding without friction down the plane.

Solution:

• Concepts:
  The moment of inertia, energy conservation, rolling
• Reasoning:
  Energy conservation:  T_f = mgh = ½mv² + ½Iω²
  For rolling ω = v/r, so T_f = ½v²[m + I/r²] = mgh.
• Details of the calculation:
  The moments of inertia of the hoop, disk, and sphere with radius r are
  I_h = mr², I_d = mr²/2 and I_sp = 2mr²/5, respectively.
  T_kin/T_f = m/[m + I/r²],  T_rot/T_f = (I/r²)/[m + I/r²] = I/[mr² + I]  
  v = [2mgh/(m + I/r²)]^½
  For a block T_rot = 0,  T_kin/T_f = 1,  v = (2gh)^½
  (a)  hoop:         T_kin/T_f = T_rot/T_f = ½,  v = (gh)^½ = ½^½v_block.
  (b)  disk:          T_kin/T_f = (2/3),  T_rot/T_f = (1/3),  v = (4gh/3)^½ = (2/3)^½v_block.
  (c)  sphere:      T_kin/T_f = 5/7,  T_rot/T_f = 2/7,  v = (10gh/7)^½ = (5/7)^½v_block.

Problem:

A sphere of radius R and uniformly distributed mass m is released at rest and begins moving down an inclined plane which makes an angle q with the horizontal.   The sphere reaches a final position as indicated, with its center at ∆z = -h relative to its initial position.  The gravitational force on the sphere is F = -mg k.

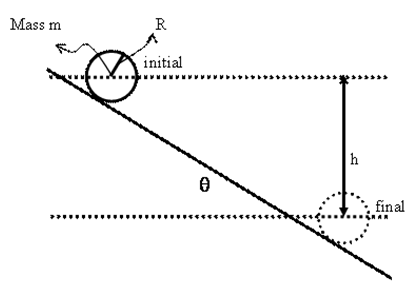
(a)  If the surface is frictionless, so the sphere slips without rotating,
    (i)  what is the time t required to go from the initial to the final position and
    (ii )  what is the final velocity of the sphere?

(b)  Now assume that the surface has sufficient friction so that the sphere rolls without slipping.  In that case, what is the final velocity of the central point of the sphere?

Solution:

• Concepts:
  Newton's 2^nd law, energy conservation
• Reasoning:
  We have a sphere sliding or rolling down an inclined plane.
• Details of the calculation:
  (a)  F = ma = m d²s/dt² = mgsinθ.  d²s/dt² = gsinθ.  v = ds/dt = gsinθt, s = ½gsinθt².
   The sphere travels a distance s = h/sinθ.   h/sinθ = ½gsinθt².  t² = 2h/(gsin²θ).
   The time t required to go from the initial to the final position is t = (2h/g)^½(1/sinθ).
   mgh = ½mv², v = (2gh)^½ is the final velocity of the sphere.
   (b)  ½mv² + ½Iw² = mgh,  I = 2mR²/5 for a uniform sphere, w = v/R for rolling.
   ½mv² + mv²/5 = mgh, 7v²/10 = gh, v = (10gh/7)^½ is the final velocity of the central point of the sphere.

Problem:

A cylindrical shell rolls without slipping down an incline as shown below.  If it starts from rest, how far must it roll along the incline to obtain a speed v?

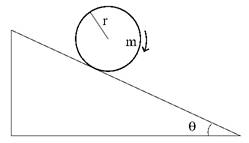
Solution:

• Concepts:
  Energy conservation, rolling
• Reasoning:
  Gravity is a conservative force.
  Rolling:  ω = v/r.  Energy conservation: ½mv² + ½Iω² = mgΔh.
• Details of the calculation:
  I = mr²,  therefore v² = gΔh. 
  Δh = Δs*sinθ, therefore Δs = v²/(g sinθ) is the distance the cylindrical shell must roll.

Problem:

A cylinder of mass m, radius r, and length l rolls straight down an inclined plane of length L and angle 30^o with respect to the horizontal.  A sphere of mass M, and radius R rolls down another inclined plane, also of length L but at an angle θ with respect to the horizontal.  Each object is solid, of uniform density, and rolls without slipping.  Find an expression for the angle θ for which the two objects reach the bottom at the same time after they are released from rest at the same time.

Solution:

• Concepts:
  Rigid-body motion, energy conservation, rolling
• Reasoning:
  The accelerations should be equal for the objects are to reach the bottom at the same time; the lengths L of the inclines does not matter.
• Details of the calculation:
  The moments of inertia are I_cyl = ½mr²,  I_sph = (2/5)Mr².  The length of the cylinder does not matter. 
  | potential energy lost|  = |kinetic energy gained|
  For the cylinder:  mgL sin(30^o) = ½mv² + ¼mr²(v²/r²) = ¾mv² = ¾m 2aL,
  a = (2/3) g sin(30^o),
  since v² - v₀² = 2aL for motion with constant acceleration.
  For the sphere:  MgL sin(θ) = ½Mv² + (1/5)Mr²(v²/r²) = (7/10)Mv² = (7/5)MaL, 
  a = (5/7) g sin(θ). 
  The acceleration does not depend on the radii and masses of the cylinder and the sphere,
  Equating  (2/3) g sin(30^o) = (5/7) g sin(θ),  sin(θ)= (14/15)sin(30^o),
  θ = sin^-1(7/15) = 27.8^o.

Problem:

An inclined plane of length L makes an angle θ > 0^o with respect to the horizontal.  A very thin ring with radius R rolls down this plane.  It reaches the bottom in time Δt_ring.
(a)  If a uniform density disk or sphere with the same radius R roll down this plane, at what time do they reach the bottom?  Find Δt_disk/Δt_ring and Δt_sphere/Δt_ring.
(b)  If all three object should reach the bottom at the same time Δt_ring, one needs to vary the angle θ for the disk and the sphere.  Find sinθ_disk/sinθ and sinθ_sphere/sinθ.

Solution:

• Concepts:
  Rigid-body motion, energy conservation, kinematics
• Reasoning:
  Energy conservation:  mgLsinθ = ½mv² + ½I(v²/r²)
  Kinematics:  v² = 2aL, a = ½gsinθ,  L = ½at²,  t = (2L/a)^½
• Details of the calculation:
  (a)  Ring:
  Energy conservation:  mgLsinθ = ½mv² + ½mr²(v²/r²),  gLsinθ = v².
  Kinematics:  v² = 2aL, a = ½gsinθ,  L = ½at²,  t = (2L/a)^½ =  (4L/(gsinθ))^½.
  Disk:
  Energy conservation:  mgLsinθ = ½mv² + ½(½mr²)(v²/r²),  gLsinθ = ¾v².
  Kinematics:  v² = 2aL, a = (2/3)gsinθ,  L = ½at²,  t = (2L/a)^½ =  (3L/(gsinθ))^½.
  Sphere:
  Energy conservation:  mgLsinθ = ½mv² + ½(2/5)mr²(v²/r²),  gLsinθ = (7/10)v².
  Kinematics:  v² = 2aL, a = (5/7)gsinθ,  L = ½at²,  t = (2L/a)^½ =  (14/(5gsinθ))^½.
  Δt_disk/Δt_ring =  (3/4)^½.
  Δt_sphere/Δt_ring = (7/10)^½.
  (b)  The same acceleration will produce the same time Δt.
  Disk:  (2/3)gsinθ_disk = ½gsinθ,  sinθ_disk/sinθ = ¾.
  Sphere:  (5/7)gsinθ_disk = ½gsinθ,  sinθ_disk/sinθ = 7/10.

Problem:

Two identical uniform cylinders of radius R each are placed on top of each other next to a wall as shown.  After a disturbance, the bottom cylinder slightly moves to the right and the system comes into motion.  Find the maximum subsequent speed of the bottom cylinder.  Neglect friction between all surfaces.

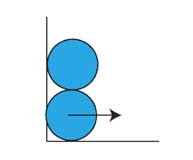
Solution:

• Concepts:
  Energy conservation
• Reasoning:
  No friction  -->  no torque
  The cylinders will not rotate.
  Assume a constraint.  The cylinders will stay in contact.
  Calculate the velocity of the bottom cylinder as a function of X, the horizontal position of its center, using energy conservation.
  Calculate its acceleration a function of X.  At the horizontal position X for which dv_x/dt = 0, the acceleration changes sign.  The force of constraint now must pull on the lower cylinder to keep the cylinders in contact.  This constraint cannot be met.  The cylinders will not stay in contact.  The lower cylinder will slide to the right with the horizontal velocity it has at the horizontal position X for which dv_x/dt = 0.  Because its acceleration and its velocity have both pointed in the positive x-direction before the cylinder reached that position X, the speed the lower cylinder has at that position is its maximum speed.
• Details of the calculation:
  

  

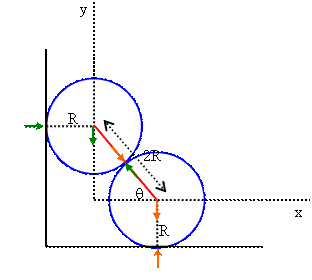
  Let M be the mass of each cylinder and R the radius.  Assume the cylinders stay in contact.
  Energy conservation:
  Mg(2R - 2Rsinθ) = ½ M(v_x² + v_y²)
  The upper cylinder is moving down and the lower cylinder is moving towards the right.
  v_x² + v_y² = 4Rg(1 - sinθ)
  X = 2Rcosθ, Y = 2Rsinθ,
  v_x = dX/dt, v_y = dY/dt, v_x² + v_y² = 4R²(dθ/dt)²
  (dθ/dt)² = (g/R)(1 - sinθ)
  Energy conservation yields dθ/dt in terms of the angle θ.  Since v_x is proportional to dθ/dt, we can now find v_x and dv_x/dt in terms of θ, and therefore find the angle θ for which dv_x/dt = 0.
  v_x = -2R sinθ dθ/dt, v_x² = 4Rg(sin²θ - sin³θ)
  dv_x²/dt = (dv_x²/dθ)(dθ/dt) = 2v_x(dv_x/dt)
  dv_x²/dt = 4Rg(2sinθ - 3sin²θ) (dθ/dt)
  dv_x/dt = dv_x²/dt = 0 if  2sinθ - 3sin²θ = 0.
  sinθ = (2/3), dθ/dt = -(g/3R)^½, v_x = (4/3)(gR/3)^½.
  The maximum speed of the bottom cylinder is (4/3)(gR/3)^½.