Impulses connecting linear and rotational motion
Problem:
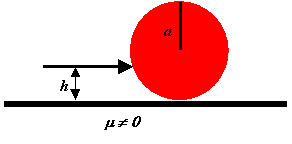
A perfectly uniform billiard ball at rest is struck by a cue at a height h.
This causes it to have an initial velocity v0 and an
initial angular velocity ω0. How far will it go on
a surface with coefficient of friction μ before pure rolling sets in?
Express your answer in terms of v0 and h.
Solution:
- Concepts:
Kinetic friction: F = μN, N = normal force. Friction
opposes the relative motion.
Rolling: A definite relationship between linear and angular velocity
is needed, and therefore a definite relationship between linear and angular
momentum.
Newton's second law: F = dP/dt,
τ = dL/dt.
- Reasoning:
At t = 0 the ball receives an impulse providing the initial velocity v0
and an angular impulse providing the initial angular velocity ω0.
If the condition for rolling is not satisfied, kinetic friction acting at a point away from the CM
will result in a torque about the
CM, thus changing the linear as well as angular momentum.
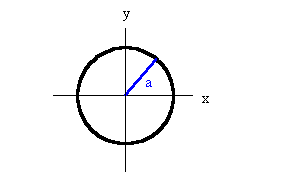
Choose the coordinate system as shown.
Let v0 = v0i and
ω0 =
ω0k. The height h at which the ball is struck
determines the relationship between v0 and the
initial angular velocity ω0.
mv0 = FΔt, Iω0 = τΔt = aFΔt(a -
h)/a.
The torque points in the z-direction if a > h and in the -z-direction if a < h.
For a sphere I = (2/5)ma2. Therefore
aω0 = (5/2)v0(a - h)/a.
The direction of the frictional force depends on v0
and ω0.
If v0 + aω0 > 0, or h < (7/5)a, the the frictional
force points in the -x-direction.
If v0 + aω0 < 0, or h > (7/5)a, the the frictional
force points in the +x-direction.
If v0 + aω0 = 0, or h = (7/5)a, the ball is rolling
and we have only static friction.
The condition for rolling is v(t) = -aω(t).
- Details of the calculation:
(i) Assume 0 < h < (7/5)a.
F = -μmgi = m(dv/dt)i. dv/dt = -μg, v(t) = v0
- μgt.
τ = I(dω/dt)k = -μmgak. dω/dt = -μmga/I,
ω(t) = ω0 - (5/2)μgt/a.
Now find the time t when v(t) = -aω(t).
v0 - μgt = -aω0
+ (5/2)μgt
t = (v0 + aω0)/((7/2)μg) is the time when rolling sets
in.
d = v0t - ½μgt2 = (12v02
+ 10aω0v0 - 2a2ω02)/(49μg)
is the distance the ball has
traveled before this time.
Inserting aω0 = (5/2)v0(a - h)/a we have
d = (12v02 + 25v02(1 - h/a) -
(25/2)v02(1 - h/a)2)/(49μg).
(ii) Assume h > (7/5)a < 2a.
F = μmgi = m(dv/dt)i. dv/dt = μg, v(t) = v0
+ μgt.
τ = I(dω/dt)k = μmgak. dω/dt = μmga/I,
ω(t) = ω0 + (5/2)μgt/a.
Now find the time t when v(t) = -aω(t).
v0
+ μgt = -aω0 - (5/2)μgt.
t = -(v0 + aω0)/((7/2)μg).
d = (-16v02 - 18aω0v0 - 2a2ω02)/(49μg).
d = (-16v02 + 45v02(h/a - 1) -
(25/2)v02(1 - h/a)2))/(49μg).
Problem:
A homogeneous thin rod of mass m and length 2a slides on a smooth, horizontal
table, one end being constrained to slide without friction in a fixed straight
line. It is initially at rest, with its extension normal to the line, when it
is struck at the free end with an impulse Q parallel to the line.
(a) Determine the initial motion of the rod.
(b) Show that the force exerted by the line on the rod is given by
Q2sinθ/[ma((4/3) - sin2θ)2], where θ is the
angle between the rod and the line.
Solution:
- Concepts:
Newton's second law: F = dP/dt,
τ
= dL/dt. The linear and the angular motion are coupled by a
constraint.
- Reasoning:
The force delivering the impulse acts at a point away from the CM. This
results in a torque about the CM. The force of constraint also acts away
from the CM and therefore can produce a torque.
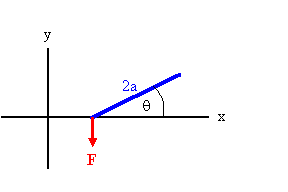
The impulse is in the x-direction. It will result in momentum
P of
the CM and angular momentum L about the CM. The force of constraint
is in the y-direction. It can change the y-component of
P and it can
change L.
The y coordinate of the CM and the angular coordinate θ are linked by
constraints.
- Details of the calculation:
(a) initial motion of CM:
P = Qi, V = (Q/m)i, initial motion about CM:
L
= -Qak, ω = -(Qa/I)k.
moment of inertia of the rod about the CM:
I = 2(m/2a)∫0ar2dr = ma2/3.
(b) subsequent motion: There is no force in the x-direction, Vx
= Q/m = constant.
There is a force in the y-direction which produces linear acceleration of
the CM and angular acceleration about the CM.
d2y/dt2 = -F/m, dL/dt = F cosθ ak = I(d2θ/dt2)k.
Therefore d2y/dt2 = -I(d2θ/dt2)/(m
cosθ a). (y is the y-coordinate of the CM.)
But y and θ are linked by constraints.
y = a sinθ, d2y/dt2 = -a sinθ (dθ/dt)2 +
a cosθ (d2θ/dt2).
Therefore - a sinθ (dθ/dt)2 + a cosθ (d2θ/dt2)
= -I(d2θ/dt2)/(m cosθ a),
d2θ/dt2 = cosθ sinθ (dθ/dt)2/[(4/3) - sin2θ]
We are supposed to show that F = Q2sinθ/[ma((4/3) - sin2θ)2].
Using F cosθ ak = I(d2θ/dt2)k, we are
supposed to show that d2θ/dt2 = (Q2/I)cosθ sinθ/[ma((4/3)
- sin2θ)2].
[To solve this differential equation guess (dθ/dt) = A/((4/3) - sin2θ)½
and verify the solution. This is an obvious guess, since the solution for F
is given. A is determined from the initial conditions.
At θ = 90o, dθ/dt = Qa/I = 3Q/ma = 3½A. A = 3½Q/ma.]
F = I(d2θ/dt2)/[cosθ a] = [ma/(3cosθ)][A2sinθ
cosθ/((4/3) -sin2θ)2] = Q2sinθ/[ma((4/3) -
sin2θ)2]
Problem:
A sphere of radius R, mass M, and radius of gyration k = (I/M)½
about any axis through its center rolls with linear velocity
v on a
horizontal plane. The direction of motion is perpendicular to a vertical step
of height h, where h < R. The sphere and step are perfectly rough and
inelastic. Show that the sphere will surmount the step upon collision if v2
> 2ghR2(R2 + k2)/(R2 - hR + k2)2.
Solution:
- Concepts:
ΔP = FΔt, ΔL =
τΔt, relationship between linear
and angular momentum for rolling motion
- Reasoning:
The sphere makes an inelastic collision with the step. It starts rotating about
the pivot point. Its momentum and angular momentum change. The change in
momentum and angular momentum are not independent of each other but are
connected by the fact that the pivot point is fixed.
- Details of the calculation:
Just after the sphere has contacted the
pivot point it is rotating about the
pivot point. Its kinetic energy is
T = ½MR2(dα/dt)2 + ½Mk2(dα/dt)2.
KE of motion of CM + KE of motion about CM
For the sphere to surmount the step we need
T > Mgh just after the sphere has contacted the pivot point.
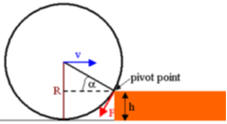
Right after contacting the step the magnitude of the momentum of the sphere is
MR(dα/dt) = Mv sinα - FΔt = Mv(R - h)/R - FΔt.
Here Mv sinα is the momentum component perpendicular to the direction from the
pivot point to the center of the sphere from before the collision and FΔt is the
impulse due to the tangential force F.
At the same time the magnitude of the angular momentum about the CM is
I(dα/dt) = Iv/R + FRΔt.
Here Iv/R is the angular momentum before the collision and FRΔt is the change in
angular momentum because of the impulse.
We therefore can write FΔt = Mv(R - h)/R - MR(dα/dt) = (I/R)(dα/dt) - Iv/R2.
Solving for (dα/dt) we have:
MR(dα/dt) = Mv(R - h)/R - (I/R)(dα/dt) + Iv/R2.
(R2 + k2)(dα/dt) = v(R - h + k2/R), (dα/dt) =
v(R2 - hR + k2)/[(R2 + k2)R].
T = ½M(R2 + k2)(dα/dt)2 > Mgh yields
½v2(R2 - hR + k2)2/[(R2
+ k2)R2] > gh,
v2 > 2ghR2(R2 + k2)/(R2 -
hR + k2)2.
Problem:
A man wishes to break a long rod of length l by hitting it on a rock.
The end of the rod which is in his hand rotates without displacement as shown in
the figure below.
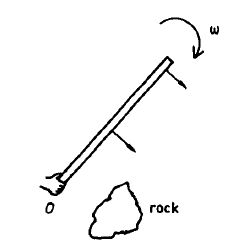
The man wishes to avoid having a large
force act on his hand at the time the rod hits the rock.
Which point on the rod should hit the rock? (Ignore gravity).
Solution:
- Concepts:
Center of percussion
- Reasoning:
When the rod hits the rock a distance x > l/2 from the point O, the rock
exerts a force of magnitude F on the rod. This force causes the CM to
accelerate backward with acceleration of magnitude dv/dt = F/m. (This
causes the point O to accelerate backward with a = dv/dt.) The force
also exerts a torque about the CM, which causes a ccw angular acceleration
about the CM of magnitude dω/dt = F(x - l/2)/I.
(This causes the point O to accelerate forward with a = (l/2)dω/dt.)
If x denotes the center of percussion, then the backward and forward
accelerations exactly cancel.
- Details of the calculation:
We want (l/2)dω/dt = dv/dt, or (l/2)F(x - l/2)/I =
F/m, (l/2)(x - l/2) = I/m.
The moment of inertia of a rod about its CM is I = ml2/12.
We want (l/2)(x - l/2)= l2/12. x = 2l/3.
The rod should contact the rock a distance x = 2l/3
from the point O.
Problem:
A uniform disk of radius R and mass M is spinning about its diameter with
angular velocity ω, as shown below. Located on the rim of the disk,
at an angle θ from the spin axis, is point P, and P is moving with speed vp.
Point P is now suddenly fixed. Show that the subsequent linear speed vc
of the center of the disk is vc = vp/5.

Solution:
- Concepts:
Newton's second law: ΔP =
FΔt, ΔL =
τΔt
- Reasoning:
To reduce the velocity of point P to zero, an impulse must
be delivered. The force acts at a point away from the CM. This results in
a torque and an angular impulse about the CM.
The impulse changes the
momentum of the CM and the angular momentum about the CM in such a way that
point P is at rest. This determines the magnitude of ΔP. The
velocity of the CM is given by vc = ΔP/M.
- Details of the calculation:
The disk rotates about the z-axis.
Assume that when it is aligned with the yz-plane the impulse is delivered to
the point P on the rim, a distance y = Rsinθ from the z-axis and z = Rcosθ
from the y-axis.
ΔP = FΔt i, ΔL =
r × ΔP
= -F R sinθ Δt k + F R cosθ Δt j.
Just after the impulse,
the momentum of the CM is ΔP and the angular momentum about the CM is
L = Izωk - F R sinθ Δt k + F R cosθ Δt j.
The velocity of the point P after the impulse is v = (FΔt/M)i +
(ω + Δω) × r = 0.
(FΔt/M)i - ω
i + (1/Iz)(F R sinθ Δt)R sinθ i + (1/Iy)(F R cosθ Δt)R cosθ
i
= 0.
For a disk of radius R we have:
Iz = Iy =
2∫0R∫0πrdrdφ(r sinφ)2ρ
= MR2/4.
Therefore:
FΔt/M - ωR sinθ + FR2sin2θ
Δt/(MR2/4) + FR2cos2θ Δt/(MR2/4)
= 0.
FΔt = (M/5)ωR sinθ .
The speed of point P before the impulse is vp
= ωR sinθ.
Therefore FΔt = (M/5)vp, vc = FΔt/M =
vp/5.






