Newton's  laws of motion applied to rigid bodies

Problem:

As shown in the figure, a uniform thin rod of weight W is supported horizontally by two supports, one at each end.  At  t = 0, one of these supports is removed.  Find the force on the remaining support immediately thereafter.

Solution:

• Concepts:
  Rigid -body motion
• Reasoning:
  Immediately after one of the supports is removed, the rod rotates about the other support.  We have acceleration of the CM and angular acceleration about the CM.  The resulting motion keeps the point resting on the other support fixed.
• Details of the calculation:
  Let the X-axis point to the right and the Y-axis point up.
  Acceleration of the CM:  W - N = -Md²Y/dt².
  Angular acceleration about CM:  N(L/2) = -Id²θ/dt².
  I = ML²/12.
  To keep the point resting on the other support fixed we need
  d²Y/dt² = (L/2)d²θ/dt².
  Therefore (W - N)/M = N(L²/4)/I = 3N/M.  W = 4N.
  N = W/4 is the magnitude of the force on the remaining support.  

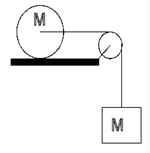
Problem:

A block with mass M hangs from a string that slides over a pulley without friction.  The other end of the string is attached to a massless axel through the center of a hoop of mass M and radius R that can roll without slipping on a flat horizontal surface.  The system is released from rest.  Find the tension in the string.

Solution:

• Concepts:
  Newton's 2nd law, linear and rotational motion, rolling
• Reasoning:
  We use Newton's 2nd law to find the linear acceleration.  The rolling constraint is used to eliminate the frictional force in the equation.
• Details of the calculation:
  For the hoop:  T - f = Ma, fR = Iα = MRa.
  For the block:  Mg - T = Ma.
  Therefore  f = Ma, T = 2Ma, Mg = 3Ma, a = g/3, T = (2/3)Mg.
  Or, using energy conservation, with the y-axis pointing down:
  MgΔy = ½Mv² + ½Mv² + ½Iω² = (3/2)Mv², gdy/dt = gv = 3vdv/dt = 3v a.
  a = g/3,  Mg - T = Ma, T = (2/3)Mg.

Problem:

Three cylinders with the same mass m, the same length h, and the same external radius R are initially resting on an inclined plane.  The coefficient of sliding friction on the inclined plane, μ, is known and has the same value for all the cylinders.  The first cylinder is an empty tube with inner radius r and density ρ₁, the second is a solid cylinder with density ρ₂, and the third has a cavity exactly like the first one, but closed with two negligible mass lids and is filled with a liquid with the same density as the cylinder's walls.  The friction between the liquid and the cylinder wall is considered negligible.  The density of the material of the first cylinder is n times greater than that of the second or of the third cylinder.
(a)  Find the condition for angle θ of the inclined plane with the horizontal, so that none of the cylinders is sliding, i.e. we have pure rolling.
(b)  Find the linear acceleration of the cylinders when we have pure rolling.  Compare these accelerations.
(c)  Find the reciprocal ratios of the angular accelerations of all three cylinders if θ is large and the condition for pure rolling is not satisfied.  Compare these angular accelerations.
(d)  Find the magnitude of the interaction force between the liquid and the walls of the third cylinder when this cylinder is sliding, given that the liquid mass is m_l.

Solution:

• Concepts:
  Rigid-body motion, linear and rotational motion, rolling
• Reasoning:
  We are asked to compare linear and angular accelerations of three cylinders when they are rolling and when they are sliding.
  (a)  For a cylinder rolling freely on an inclined plane the equations of motion are
  mg sinθ - F_f = ma,  F_fR = Iα,
  where α is the angular acceleration. The condition for rolling is a = αR.
  Solving the system of equations we find
  a = g sinθ/(1 + I/(mR²)),  F_f =  mg sinθ/(1 + mR²/I).
  The condition of non-sliding is  F_f < μN, where the normal force N = mgcosθ.
• Details of the calculation:
  (a)  Using F_f from above we need mg sinθ < μmg cosθ(1+ mR²/I),  tanθ < μ(1+ mR²/I). 
  For none of the cylinders to slide, we have to use the largest moment of inertia I.
  The moments of inertia of the three cylinders are
  I₁ = ½ρ₁π(R⁴ - r⁴)h,  I₂ = ½ρ₂πR⁴h, I₃ = ½ρ₂π(R⁴ - r⁴)h.
  Because the three cylinders have the same mass we have
  m = ρ₁π(R² - r²)h = ρ₂πR²h, which results in
  r² = R²(1 - ρ₂/ρ₁) = R²(1 - 1/n) with n = ρ₁/ρ_2.
  The moments of inertia can be written as I₁ = I₂(2 - 1/n),  I₃ =  I₂(2 - 1/n)(1/n) = I₁/n.
  We have ρ₁ > ρ₂,  n > 1, and therefore  I₁ > I₂ > I₃.  
  The necessary condition for none of the cylinders to slide is tanθ < μ(1+ mR²/I₁).     
  (b)  The linear accelerations of the rolling cylinders are
  a₁ = 2g sinθ/[4 - 1/n],  a₂ = 2g sinθ/3, a₃ = 2g sinθ/[2 + 2/n - 1/n²].
  a₁ < a₂ < a₃.
  (c)  If the condition for pure rolling is not satisfied we have F_f = μN = μmg cosθ and α = (R/I) μmg cosθ
  For the cylinders of this problem we have α₁ : α₂ : α₃ = 1/I₁ : 1/I₂ : 1/I₃ = 1 : (2 - 1/n) : n.
  1/α₁ : 1/α₂ : 1/α₃ = I₁ : I₂ : I₃ = 1 : 1/(2 - 1/n) : 1/n.
  α₁ < α₂ < α₃.
  (d)  When the cylinders is sliding we have mg sinθ - F_f = ma,  F_f = μmg cosθ,  a = g(sinθ - μ cosθ).
  Let F be the interaction force between the liquid and the walls acting on the liquid mass m_l inside the cylinder.

  

  F_x + m_l gsinθ = m_la = m_lg(sinθ - μ cosθ),  F_y - m_lg cosθ = 0.
  F_x = -μ m_lgcosθ,  F_y = m_lg cosθ,
  F = (F_x² + F_y²)^½ = m_lg cosθ (1 + μ²)^½.

Problem:

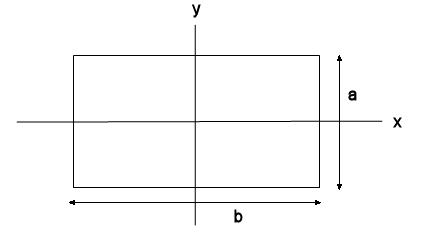
A uniform rectangular object of mass m with sides a and b (b > a) and negligible thickness rotates with constant angular velocity ω about a diagonal through the center.  Ignore gravity.

(a)  What are the principal axes and principal moments of inertia?
(b)  What is the angular momentum vector in the body coordinate system?
(c)  What external torque must be applied to keep the object rotating with constant angular velocity about the diagonal?

Solution:

• Concepts:
  Rigid-body motion, the moment of inertia tensor
• Reasoning:
  The body is not rotating about one of its principal axes. 
• Details of the calculation:
  (a)  The principal axes are the symmetry axes. To find the angular momentum L = I₁ω₁i + I₂ω₂j + I₃ω₃k we have to find the moments of inertia and the angular velocity components along the principal axes.
  
  I₁ = I_x = ma²/12,   I₂ = I_y = mb²/12,   I₃ = I_z = I₁ + I₂ = m(a² + b²)/12.
  (b) The component of ω along the principal axes are
  ω₁ = ωb/(a² + b²)^½,  ω₂ = ωa/(a² + b²)^½,  ω₃ = 0.  ω = [ω/(a² + b²)^½] (b, a, 0).
  L = I₁ω₁i + I₂ω₂j + I₃ω₃k = [mabω/(12(a² + b²)^½)] (a, b, 0).  (Note: i, j, k refer to the body-fixed axes.)
  (c)  Let dL/dt be the rate of change of L with respect to the space fixed axes, d'L/dt its rate of change with respect to the body fixed axes.
  dL/dt = d'L/dt + ω × L = τ.  In the body-fixed coordinate system ω is constant,  d'L/dt = 0.
  τ = ω × L = (ω₁L₂ - ω₂L₁)k = [mabω²/(12(a² + b²))](b² - a²)k.  (Note: k points along the body-fixed z-axis)
  

Problem:

Near the surface of the earth a uniform disk of mass M₁ and radius R is pivoted on a frictionless horizontal axle through its center.  A small mass M₂ is attached to the disk at radius R/2, at the same height as the axle.  This system is released from rest.

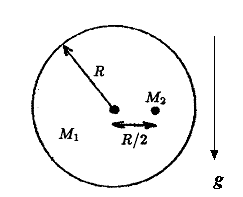
(a)  What is the angular acceleration of the disk immediately after it is released?
(b)  What will be the magnitude of the maximum angular velocity that the disk will reach?

Solution:

• Concepts:
  The moment of inertia, Newton's 2^nd law applied to rotational motion, energy conservation
• Reasoning:
  The system is constrained to rotate about a fixed axis, gravity is responsible for a torque about this axis, the force of gravity is a conservative force.
• Details of the calculation:
  (a)  The moment of inertia of the disk about its center is I_disk = ½M₁R².
  The total moment of inertia of the system about the center of the disk is
  I = I_disk + M₂(R/2)² = (2M₁ + M₂)R²/4.
  When the system is released the torque is τ = Iα = M₂gR/2.
  The angular acceleration α when the system is released therefore is
  α = M₂gR/2I, = 2M₂g/[(2M₁ + M₂)R].
  (b)  Energy conservation:  ½Iω_max² = M₂gR/2.
  ω_max² = M₂g R/I = 4M₂g/[(2M₁ + M₂)R].

Problem:

A dumbbell consists of two spheres A and B, each with volume V, which are connected by a rigid rod.  A has mass M and B has mass 2M.  The distance between the centers of the spheres is d as shown below.  In all parts of this problem assume that the mass and volume of the rod and the moment of inertia of each sphere about its diameter are so small that they can be taken to be zero, and that air resistance can be neglected.

• (a)  True or false?
  If the dumbbell is dropped in a vacuum with the rod initially horizontal, the heavier sphere B will hit the floor first.
• (b) True or false?
  If the dumbbell is thrown on a frictionless horizontal surface with the rod horizontal, sphere B will move in a straight line with A rotating about it.
• (c)  What is the moment of inertia of the dumbbell about an axis, which passes through the center of mass of the dumbbell and is perpendicular to the rod?
• (d)  The dumbbell is placed on a frictionless horizontal table.  Sphere A is attached to a frictionless pivot so that B can be made to rotate about A with constant angular velocity.
  
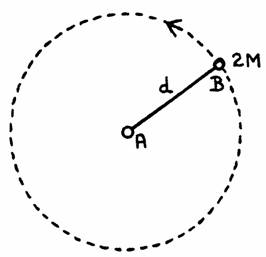
  If B makes one revolution in period T, what is the tension in the rod?
• (e)  Sphere A is now attached to a frictionless pivot so that B hangs freely vertically.  At some instant of time a strong wind begins to apply a constant horizontal force to B.  As a result, the dumbbell rotates about A in a vertical plane.
  
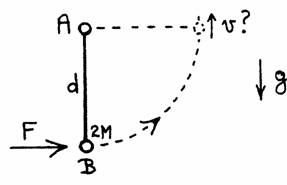
  What is the speed of B (in terms of F, d, g, and M) at the instant when the dumbbell is horizontal?
• (f)  The dumbbell is placed in water, which has density ρ.  It is observed that by attaching a mass m to the rod, a distance l from the center of B, the dumbbell floats with the rod horizontal on the surface of the water and each sphere exactly half submerged, as shown below.  The volume of the mass m is negligible.  In terms of V, M, d, and ρ, derive the value of m and the value of l.
  

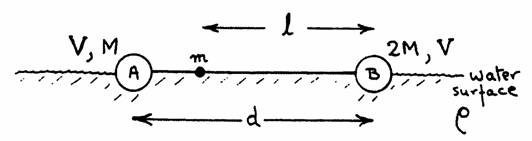
Solution:

• Concepts:
  Various concepts and definitions introduced in a general physics course, such as Newton's second law, torque, buoyant force, moment of inertia, etc.
• Reasoning
  The different parts of the problem test the student's understanding of some of the fundamental concepts introduced in a typical general physics course.
• Details of the calculation:
  (a)  False:  The only force acting on the dumbbell is gravity, giving mass-independent acceleration g.
  (b)  False:  The CM will move in a straight line.  Both spheres may rotate about the CM with angular frequency ω₀, if ω₀ ≠ 0.
  (c)  Location of the CM:  MR = 2M(d - R), R = distance of CM from sphere A,
  R = (2/3)d.
  Moment of inertia: I = M(2d/3)² + 2M(d/3)² = (2/3)Md².
  (d)  The tension must provide the centripetal force, F_c = 2Mv²/d.
  v = 2πd/T, F_c = 8Mπ²d/T².
  (e)  The tangential component of the applied horizontal force is F_t = Fcosθ.
  The tangential component of the gravitational force is 2Mgsinθ.
  The magnitude of the torque pointing out of the page is
  τ = Fdcosθ - 2Mgdsinθ = Iα.  (I = moment of inertia, I = 2Md², α = angular acceleration.)
  ½Iω² = ∫τdθ.
  ω² = 2(Fd - 2Mgd)/I = (Fd - 2Mgd)/(Md²).
  But ω² = v²/d².  v = [(Fd - 2Mgd)/M]^1/2.
  We can a also use the work-kinetic energy theorem.
  Total work done by external forces: W = Fd - 2Mgd = ½2Mv².
  (f) The system is at rest, the total force and the total torque are zero.
  No force:  ½ρVg + ½ρVg - Mg - 2Mg - mg = 0, m = ρV - 3M.
  (buoyant force + gravitational force = 0)
  No torque about sphere B: (½ρVg  - Mg )d - mgl = 0.
  l = (½ρVd  - Md)/(ρV - 3M) = (m + M)d/(2m).

Problem:

Suppose a uniform wheel of radius R, thickness d, and mass M is rotating with uniform angular speed ω about an axis that passes through its center of mass but makes an angle θ with a line perpendicular to the wheel.  Find the angular momentum of the wheel and the torque about the principal axes.

Solution:

• Concepts:
  Rigid body motion, Euler's equations
• Reasoning:
  Euler's equations give us the relationships between torque, angular acceleration and angular velocity about the principal axes.
• Details of the calculation:
  Orient the body-fixed coordinate system so that the z-axis is perpendicular to the wheel, and ω lies in the xz-plane. Then ω_x = ωsinθ, ω_y = 0, ω_z = ωcosθ.  Euler's equations are
  I_xdω_x/dt + (I_z - I_y)ω_yω_z = τ_x,  I_ydω_y/dt + (I_x - I_z)ω_zω_x = τ_y,  I_zdω_z/dt + (I_y - I_x)ω_xω_y = τ_z.
  dω_x/dt = dω_y/dt = dω_z/dt = 0.  ω_y = 0.
  τ_x = τ_z = 0.
  (I_x - I_z)ω_zω_x = τ_y,  (I_x - I_z)ω²sinθcosθ = τ_y,  (I_x - I_z)ω²(sin2θ)/2 j = τ = torque about the y-axis.
  For a cylinder of radius R, height d, and mass M we have
  I_z = M/(πr²d)∫_-d/2^d/2dz∫₀^R2πr³dr = MR²/2,
  I_x = M/(πr²d)∫_-d/2^d/2dz∫₀^2πdθ∫₀^Rrdr(r²sin²θ + z²) = Md²/12 + MR²/4 = I_y.
  τ = (Md²/12 - MR²/4)ω²(sin2θ)/2 j.
  
  L = i I_xωsinθ + k I_zωcosθ.  Here i and k refer to the body fixed axis.
  L = i (Md²/12 + MR²/4)ωsinθ + k (MR²/2)ωcosθ.

Problem:

A pair of long, thin, rods, each of length L and mass M, are connected to a hoop of mass M and radius L/2 to form a 4-spoked wheel as shown.
Express all answers in terms of the given variables and  fundamental constants.
(a)  Calculate the moment of inertia for the entire spoked-wheel assembly for an axis of rotation through the center of the assembly and perpendicular to the plane of the wheel.

The wheel is now mounted to a frictionless fixed axle and suspended from a vertical support.  Several turns of light cord are wrapped around the wheel, and a mass M is attached to the end of the cord and allowed to hang.  The mass is released from rest.
(b)  Determine the tension in the cord supporting the mass as it accelerates downwards.
(c)  Calculate the angular acceleration of the wheel as the mass descends.
(d)  Determine the instantaneous velocity of the mass after the wheel has turned one revolution.
(e)  Determine the instantaneous angular momentum of the mass-wheel system about the center of the wheel after the wheel has turned one revolution.

Solution:

• Concepts:
  Newton's second law, linear and rotational motion
• Reasoning:
  We use Newton's 2^nd law to find the tension.
• Details of the calculation:
  (a)  The moment of inertia for the spoked wheel is the sum of the individual moments of inertia of its three components,  I_wheel = 2I_rod + I_hoop.
  I_wheel = 2ML²/12 + MR² = 2ML²/12 + M(L/2)² = 5ML²/12.
  (b)  For the hanging mass:  F_net = Mg - T = Ma.
  For the wheel:  τ = (L/2)T = Iα = (5ML²/12)(2a/L).
  a = 3T/(5M),  T = 5Mg/8.
  (c)  a = 3T/(5M) = 3g/8,  α = 2a/L = (3/4)g/L.
  (d)  v_f² = v_i² + 2aΔy.  Here v_f² = 2(3g/8))(2πL/2) = 3gπL/4,  v_f = (3gπL/4)^½.
  (e)  L_system = L_mass + L_wheel = M(L/2)v_f + I_wheel 2v_f/L = ML (4gπL/3)^½.