Rotational kinematics

Problem:

A centrifuge in a medical laboratory rotates at an angular speed of 3600 rev/min.  When switched off, it rotates 50 times before coming to rest.  What is the constant angular acceleration of the centrifuge?

Solution:

• Concepts:
  Rotational kinematics
• Reasoning:
  We have motion with constant angular acceleration.
• Details of the calculation:
  Formulas for rotational kinematics:
  ω = dθ/dt,  α = dω/dt,  Δω = αΔt,  ω_f = ω_I + αΔt.
  θ_f = θ_i + ω_i(t_f - t_i) + ½α(t_f - t_i)².
  Δθ = <ω>Δt.  <ω> = (ω_i + ω_f)/2
  Given:
  θ_i = 0,  θ_f = 50 * 2π (50 revolutions)
  ω_i = (3600 * 2π/min) *(1 min/60 s) = 377/s,  ω_f = 0
  α = constant
  Asked:
  α = ?
  Find Δt:  <ω> = (ω_i + ω_f)/2 = 188.5/s,  Δt = Δθ /<ω> = 1.667 s
  Find α:  α = (ω_f - ω_i)/ Δt = -(377/s)/(1.666 s) = -226.2/s²

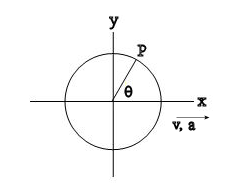
Problem:

An automobile drag racer drives a car with constant acceleration ai.  The tires with radius r₀ are not slipping.  At t = 0 the car starts from rest.
(a)   Derive an equation for the acceleration of a point P(θ) on the outer surface of the tire when the instantaneous velocity of the car is vi.
(b)   For which point P(θ) on the outer surface of the tire is the magnitude of the acceleration the greatest?  What is this magnitude of the acceleration?

Solution:

• Concepts:
  Rigid body motion
• Reasoning:
  Let a_i denote the acceleration of the point P.
  a_i = a + a_rel, where a is the acceleration of the CM and a_rel is the acceleration of P in the CM frame
• Details of the calculation:
  (a)  a_i = ai + a_tangential + a_centripetal = ai + a(-cosθ j + sinθ i) - (v²/r₀) (cosθ i + sinθ j)
  = (a + a sinθ - (v²/r₀)cosθ)i - (a cosθ  + (v²/r₀) sinθ)j.
  (b)  a_i is largest when the acceleration of the CM and the acceleration of P in the CM frame both point in the same direction.  This can happen for a point P in the second quadrant, when a cosθ_m + (v²/r₀) sinθ_m = 0, tanθ_m = -ar₀/v², tan(π - θ_m) = ar₀/v².
  This identifies the point of maximum acceleration.
  Substituting a cosθ_m = -(v²/r₀) sinθ_m yields a_im = (a + a sinθ_m - (v²/r₀)cosθ_m)i.
  a_im  = a + a sinθ_m - (v²/r₀)cosθ_m = a + [a² + (v²/r₀)² ]^½.
  (Since at P(θ_m) the acceleration of the CM and the acceleration of P in the CM frame point in the same direction, their magnitudes just add.)