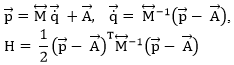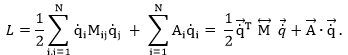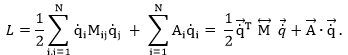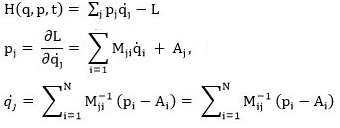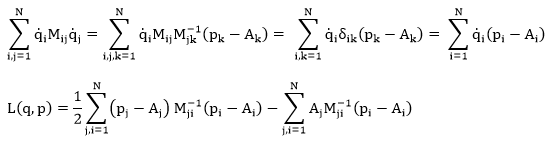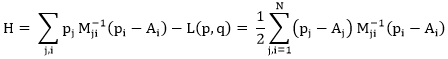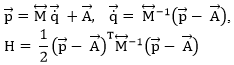Lagrangian and Hamiltonian formalism

Problem:

The Lagrangian of a system is given by L({q_i, v_i}), where {qi} are linearly independent generalized coordinates and {v_i = dq_i/dt} are the generalized velocities.
d/dt(∂L/∂v_i) - ∂L/∂q_i = 0,  ∂L/∂v_i  = p_i.
A symmetry is a coordinate transformation that does not change the form of the Lagrangian.
Consider a continuous coordinate transformation, which is a transformation that can be built from infinitesimal transformations of the form  {q_i --> q_i' = q_i  + δq_i}, with δq_i = f({q_i})ε,
where ε --> 0.  Show that if the Lagrangian is invariant under this transformation (δL = 0), then the quantity Q = ∑ p_i f({q_i}) is a constant of motion, i.e. a conserved quantity.

Solution:

• Concepts:
  Lagrangian mechanics
• Reasoning:
  δL({q_i, v_i}) = ∑[(∂L/∂v_i) δv_i - ∂L/∂q_i) δq_i]
• Details of the calculation:
  δL = ∑[p_i δv_i - ∂L/∂q_i) δq_i].
  From Lagrange's equations  ∂L/∂q_i = dp_i/dt.
  δL = ∑[p_i δ(dq_i/dt) - (dp_i/dt)) δq_i] = ∑[p_i d(δq_i)/dt  -  (dp_i/dt)) δq_i] = d/dt∑ [p_i δq_i]
  Note:  δ(dq_i/dt) = d(δq_i)/dt 
  δL = 0 --> ∑ [p_i δq_i] = constant.

Problem:

Let {q_i} and {p_i} be the generalized coordinates and momenta of a system and let A, B,  and C be arbitrary functions of the q's and p's.
The Poisson Bracket (PB) of A and C is defined as
{A, C} = ∑_i [(∂A/∂q_i) (∂C/∂p_i) - (∂A/∂p_i) (∂C/∂q_i)].

Properties of the PB that can be easily verified are
{A, C} = -{C, A},  {kA, C} = k{A, C} for any constant k.
{(A+B), C} = {A, C} + {B, C}.
{(AB), C} = A{B, C} + B{A, C}

(a)  Evaluate {q_i, q_j}, {p_i, p_j}, and {q_i, p_j} for arbitrary i, j.
(b)  Evaluate {q_iⁿ, p_i}.  (Hint: use mathematical induction)
(c)  Evaluate {F, p} for an arbitrary smooth function F of the generalized coordinate q.
(Any smooth function can be arbitrarily well approximated by a polynomial.)

Solution:

• Concepts:
  Poisson Bracket
• Reasoning:
  We are asked to evaluate various Poisson Brackets.
• Details of the calculation:
  (a)  {q_i, q_j} = 0,  {p_i, p_j} = 0,  {q_i, p_j} = δ_ij.
  (b)  {q_i², p_i} = 2 q_i {q_i, p_i}= 2 q_i
  {q_iⁿ, p_i} = n q_i^n-1, for n = 2.
  Assume {q_i^n-1, p_i} = (n-1) q_i^n-2.
  Then {q_iⁿ, p_i} = q_i{q_i^n-1, p_i} + q_i^n-1{q_i, p_i} = (n-1) q_i^n-1 + q_i^n-1 = n q_i^n-1.
  {q_iⁿ, p_i} = n q_i^n-1 therefore holds for all n.
  (c)   F(q) = ∑_n A_nqⁿ.  {F, p} = ∑_n A_n{qⁿ, p} = ∑_n A_n n q_i^n-1 = dF/dq.
  {F, p} = dF/dq.

Problem:

Let {q_i} and {p_i} be the generalized coordinates and momenta of a system and let F, and G be arbitrary functions of the q's and p's.
The Poisson Bracket (PB) of F and G is defined as
{F, G} = ∑_i [(∂F/∂q_i) (∂G/∂p_i) - (∂F/∂p_i) (∂G/∂q_i)].
(a)  Show that dq_j/dt = {q_j, H},  dp_j/dt = {p_j, H} is another way of writing Hamilton's equations of motion.
(b)  Write dF/dt in terms of a PB.
(c)  Consider the three Cartesian components of the angular momentum L. 
We have {Li, Lj} = ∑_k ε_ijk L_k.
Assume the Hamiltonian of a system is given by H = ωL_z.  Use the Poisson Bracket formulation to work out the equations of motion for the vector L.

Solution:

• Concepts:
  Poisson Bracket formulation of classical mechanics
• Reasoning:
  We are asked to show how the PB formalism can be used to find the evolution of a physical quantity.
• Details of the calculation:
  (a)  {q_j, H} =  ∑_i [(∂q_j/∂q_i) (∂H/∂p_i) - (∂q_j /∂p_i) (∂H/∂q_i)] = ∂H/∂p_j
  dq_j/dt = ∂H/∂p_j
  {p_j, H} = ∑_i [(∂q_j/∂q_i) (∂H/∂p_i) - (∂q_j /∂p_i) (∂H/∂q_i)] = -∂H/∂q_j
  dp_j/dt = -∂H/∂q_j
  (b)  dF/dt = ∑_i [(∂F/∂q_i) (dq_i/dt) + (∂F/∂p_i) (dp_i/dt)]
  (dq_i/dt) = (∂H/∂p_i),  (dp_i/dt) = -(∂H/∂q_i)
  dF/dt = ∑_i ((∂F/∂q_i) (∂H/∂p_i) - (∂F/∂p_i) (∂H/∂q_i)) = {F, H}
  (c)  dL_i/dt = {L_i, H} = ω{L_i, L_z}
  dL_z/dt = 0.
  dL_x/dt = -ωL_y. 
  dL_y/dt = ωL_x. 
  L_x = A cos(ωt + φ)
  L_y = A sin(ωt + φ)
  The z-component of L does not change.  The component of L perpendicular to the z-axis in the xy-plane rotate ccw about the origin with constant angular velocity ω = ωk.

Problem:

Assume every point in phase space is shifted by an amount δq_i = {q_i,G}, δp_i = {p_i,G}, where G is an arbitrary function of the coordinates and conjugate momenta.  
G is called the generator of the transformation δq_i, δp_i.
Show that the function of the coordinates and conjugate momenta F is changed by an amount δF = {F,G} by the transformation.

Solution:

• Concepts:
  Poisson Bracket formulation of classical mechanics
• Reasoning:
  We are asked to explore the connection between symmrtry and conservation laws.
• Details of the calculation:
  δF = (∂F/∂q_i) δq_i + (∂F/∂p_i) δp_i  (summation convention)
  δF = (∂F/∂q_i) {q_i,G},  + (∂F/∂p_i) {p_i,G} = {F, G}   (show by writing out all the terms in the PB)
  When the transformation generated by G does not change the Lagrangian or Hamiltonian, then   δH = {H, G} = 0. 
  Assume G is such a symmetry transformation.  Find dG/dt.
  dG/dt = (∂G/∂q_i) (∂q_i/∂t)  + (∂G/∂p_i) (∂p_i/∂t)  = (∂G/∂q_i) (∂H/∂p_i) - (∂G/∂p_i) (∂H/∂q_i) = {G,H}
  dG/dt = 0.  If G generates a symmetry transformation, the G is a constant of motion.

Problem:

Consider the motion of a particle in a potential U(r) in a rotating frame.  Let Ω be the angular velocity of the rotating frame with respect to an inertial frame and let Ω be constant.
(a)  Express the Lagrangian of the particle in terms of r and v of the particle in the rotating frame.
(b)  Obtain the equations of motion in the rotating frame.
(c)  Obtain the Hamiltonian of the particle in the rotating frame.

Solution:

• Concepts:
  Lagrangian and Haniltonian mechanics, rotating frames
• Reasoning:
  We are asked to write down the lagrangian and the Hamiltonian in the rotating frame and to obtain the equations of motion in the rotating frame.
• Details of the calculation:
  (a)  L = T - U.  In the inertial frame L = ½mv_i² - U(r).
  The relationship between the velocity v_i in the inertial frame and the velocity v in a frame rotating with constant angular velocity Ω is
  v_i = v + Ω × r.
  In terms of r and v in the rotationg frame L = ½m(v + Ω × r)² - U(r), or
  L = ½mv² + ½m(Ω × r)² + mv·(Ω × r) - U(r),
  (b)  ∂L/∂v = mv + m(Ω × r)
  (d/dt)∂L/∂v = mdv/dt + m(Ω × v)
  ∂L/∂r = (∂/∂r)(½m(Ω × r)² + mv·(Ω × r) - U(r))
  d(Ω × r)² = 2(Ω × r)·(Ω × dr) = 2[(Ω × r) × Ω]·dr
  (∂/∂r)(Ω × r)² = 2[(Ω × r) × Ω] = -2[(Ω × (Ω × r)]
  (∂/∂r)(v·(Ω × r)) = (∂/∂r)[(v × Ω)·r] = (v × Ω) = -(Ω × v)
  The equation of motion is (d/dt)∂L/∂v = ∂L/∂r.
  mdv/dt + m(Ω × v) = -m[(Ω × (Ω × r)] - m(Ω × v) - ∂U(r)/∂r
  mdv/dt = - ∂U(r)/∂r - m[(Ω × (Ω × r)] - 2m(Ω × v)
  is the equation of motion in the rotating frame.
  -2m(Ω × v) = Coriolis force
  -m Ω × (Ω × r) = centrifugal force
  (c)  p = ∂L/∂v = mv + m(Ω × r), v = (p - m(Ω × r))/m
  H = p·v - L
  H(p, r) = p·(p - m(Ω × r))/m - ½(p - m(Ω × r))²/m - ½m(Ω × r)² - (p - m(Ω × r))·(Ω × r) + U(r)
  = p²/m - p·(Ω × r) - p²/(2m) -  ½m(Ω × r))² + p·(Ω × r)
  - ½m(Ω × r)² - p·(Ω × r) + m(Ω × r))² + U(r)
  = p²/(2m) - p·(Ω × r)  + ½m(Ω × r))² - ½m(Ω × r)² + U(r)
  H(p, r) = (p - m(Ω × r))²/(2m)  - ½m(Ω × r)² + U(r)
  is the Hamiltonian of the particle in the rotating frame.

Problem:

The Lagrangian of a system of N degrees of freedom is

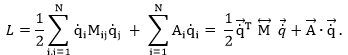
What is the Hamiltonian for a symmetric mass matrix M_ij = M_ji?

Solution:

• Concepts:
  The Lagrangian and the Hamiltonian
• Reasoning:
  Given the Lagrangian, we are asked to find the Hamiltonian of a system.
• Details of the calculation:
   

  

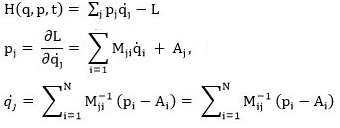
  Therefore:

  

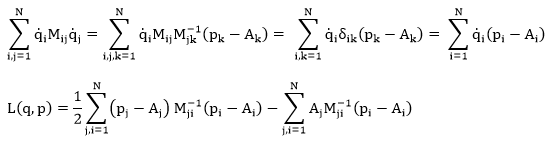
  We then have:

  

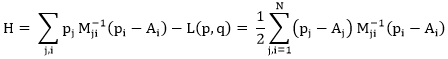
  In matrix notation: