Problems involving the Hamiltonian

Problem:

In a problem with one degree of freedom, a particle of mass m is subject to a force F(x,t) = F₀t.  The force is derivable from a potential.
(a)  Find the potential energy of the particle and the Lagrangian and Hamiltonian of the particle.
(b)  Solve Hamilton's equations of motion.

Solution:

• Concepts:
  The Lagrangian and the Hamiltonian, Hamilton's equations of motion
• Reasoning:
  We are asked to find the Lagrangian and the Hamiltonian and to solve Hamilton's equations of motion.
• Details of the calculation:
  (a)  F(x,t) = -∂U/∂x = F₀t,  U(x,t) = -F₀tx. (We can arbitrarily choose the zero of the potential energy.)
  L = T - U = ½m(dx/dt)² + F₀tx.  ∂L/∂(dx/dt) = p_x = m(dx/dt).
  H = (dx/dt)p_x - L = p_x²/2m - F₀tx.
  (b) dx/dt = ∂H/∂p_x,  dp_x/dt = -∂H/∂x,  dx/dt = p_x/m, dp_x/dt = F₀t,  d²x/dt² = F₀t/m.
  dx/dt = F₀t²/(2m) + v₀,  x =  F₀t³/(6m) + v₀t + x₀.

Problem:

A block of mass m moves on a frictionless surface with a displacement x under the influence of a spring force F = -kx,  where k is the spring constant.
(a)  Calculate the potential energy U(x), and the Lagrangian.
(b)  Find Lagrange's equations of motion.
(c)  Find the Hamiltonian.
(d)  Find Hamilton's equations of motion.

Solution:

• Concepts:
  Lagrange's and Hamilton's Equations
  d/dt(∂L/∂(dq_i/dt)) -  ∂L/∂q_i = 0.
  ∂L/∂(dq_i/dt) = p_j.  H(q, p, t) = ∑_i(dq_i/dt)p_i - L.
  dq_i/dt = ∂H/∂p_i,  dp_i/dt = -∂H/∂q_i/
• Reasoning:
  F is a conservative force.  It is derivable from a potential.  We can use the Lagrangian and Hamiltonian formalism.
• Details of the calculations:
  (a)  Hooke's law:  U = ½kx²,  L = T - U = ½m(dx/dt)² - ½kx².
  (We have one generalized coordinate.)
  (b)  ∂L/∂(dx/dt) = m(dx/dt),  ∂L/∂x = kx,  d²x/dt² = -(k/m)x.
  (c)  P_x = ∂L/∂(dx/dt) = m(dx/dt).
  m(dx/dt)² - L = ½m²(dx/dt)² + ½kx² = P_x²/(2m) + ½kx².
  H = P_x²/(2m) + ½kx².
  (d) dx/dt  = ∂H/∂P_x = P_x/m,  dP_x/dt = -∂H/∂x = -kx.

Problem:

A point particle of mass m is constrained to move in one dimension on the x-axis.
The force acting on the particle can be derived from the velocity-dependent potential
U = F(dx/dt)t.
Write down
(a)  the Lagrangian,
(b)  the Hamiltonian,
(c)  Hamilton's equations.

Solution:

• Concepts:
  The Lagrangian and the Hamiltonian, Hamilton's equations of motion
• Reasoning:
  We are asked to find the Lagrangian and the Hamiltonian and Hamilton's equations of motion for a particle, given that force acting on the particle it can be derived from a generalized potential U = F(dx/dt)t.
• Details of the calculation:
  (a)  T = ½m(dx/dt)² ,  U = F(dx/dt)t,  we have a velocity-dependent potential.
  L = ½m(dx/dt)² - F(dx/dt)t.
  (b)  p_x = ∂L/∂(dx/dt) = m(dx/dt) - Ft.
  dx/dt = (p_x + Ft)/m.
  H = (dx/dt)p_x - L
  = p_x(p_x + Ft)/m - (p_x + Ft)²/(2m) + Ft(p_x + Ft)/m
  = (p_x + Ft)²/(2m).
  The Hamiltonian is a function of the coordinates and the canonical momenta.
  (c)  Hamilton's equations:
  dx/dt  = ∂H/∂p_x = (p_x + Ft)/m,  dp_x/dt = -∂H/∂x = 0.
  This yields the second order differential equation for the coordinate x,
  d²x/dt² = F/m.

Problem:

A particle of mass m moves in one dimension under the influence of a force

F(x,t) = -k x exp(-t/τ),

where k and τ are positive constants.  (Note carefully the dependence on x to the first power).
(a)  Compute the Lagrangian function.
(b)  Use Lagrange's equation to determine the equation of motion explicitly.
(c)  Compute the Hamiltonian function in terms of the generalized coordinate and generalized momentum.  (Show clearly how you get this.)
(d)  Determine Hamilton's equations of motion explicitly for this particular problem (not just general formulae).
(e)  Does the Hamiltonian equal the total energy?
(f)  Is the total energy of the mass conserved?
(g)  What is it about the force F which supports your answer to part f?

Solution:

• Concepts:
  Lagrangian and Hamiltonian mechanics
• Reasoning:
  We are asked to find the Lagrangian and Hamiltonian for the system.
• Details of the calculation:
  (a)  F(x,t) = - ∂U(x,t)/∂x.   U(x,t) = k(x²/2)exp(-t/τ).
  L = T - U = ½ m(dx/dt)² -  k(x²/2)exp(-t/τ).
  (b)  d/dt(∂L/∂(dx/dt)) -  ∂L/∂x = 0. 
  ∂L/∂(dx/dt) = m dx/dt,  d/dt(∂L/∂(dx/dt)) = m d²x/dt².
  ∂L(x,t)/ ∂x = -kxexp(-t/τ).
  m d²x/dt² = -kx exp(-t/τ).
  
  (c)  H(x, p, t) = (dx/dt)p - L.
  p = ∂L/∂(dx/dt)= m dx/dt.   H = p²/(2m) + k(x²/2)exp(-t/τ).
  (d) dx/dt  = ∂H/∂p = p/m.  dp/dt  = -∂H/∂x = -kxexp(-t/τ).
  d²x/dt²= (dp/dt)/m = -(k/m)xexp(-t/τ).
  (e)  Yes.  If the generalized coordinates do not explicitly depend on time, then H = T + U = E, the total energy of the system.
  (f)  No.  If H does explicitly depend on time, H = H(t), then H is not a constant of motion.
  (g)  The force F is a function of position and time.  It is derivable from a time dependent potential energy function.  F = -k(t)x, it is a Hooke's law type force with a spring constant that decreases exponentially.  Assume a particle has kinetic energy E₀ = ½mv₀² as it moves through the origin at t = 0 and comes to a stop at position x.  It then accelerates back towards the origin.  Since the magnitude of the force decreases with time, the magnitude of the positive work done by F on the return trip is smaller than the magnitude of the negative work done by F on the trip from the origin to x.  The potential energy at the origin is zero, the kinetic energy of the particle has decreased, the particle has lost energy.

Problem:

The Lagrangian for a simple spring is given by  L = ½m(dx/dt)² - ½kx².
Find the Hamiltonian and the equations of motion using the Hamiltonian formulation.  Identify any conserved quantities.

Solution:

• Concepts:
  The Lagrangian and the Hamiltonian, Hamilton's equations of motion
• Reasoning:
  We are asked to find the Lagrangian and the Hamiltonian and Hamilton's equations of motion.
• Details of the calculation:
  H = p²/(2m) + ½kx².  H is a function of x and p, while the Lagrangian is a function of x and v.
  Equations of motion: dx/dt = ∂H/∂p,  dp/dt = -∂H/∂x.
  dx/dt = p/m,  dp/dt = -kx.  We have two first-order differential equations which can be combined to yield the second order differential equation d²x/dt² = -(k/m)x.
  The coordinates and the Hamiltonian do not contain time explicitly, so H = E, and E = constant.  The energy E is a conserved quantity.

Problem:

Consider the Lagrangian L = m(dx/dt)(dy/dt) - mω₀²xy.
(a)  Write down Lagrange's equations associated with this Lagrangian and solve them.  What physical system does this Lagrangian describe?
(b)  Determine the Hamiltonian of the system.
(c)  Define new generalized coordinates x' and y' such that
x = 2^-½ (x' + iy'), y = 2^-½ (x' - iy'). 
Write down the Lagrangian and Lagrange's equations in terms of the new generalized coordinates and velocities and solve them.
(d)  Express the total energy of the system in terms of the new generalized coordinates and velocities, assuming these coordinates are real.

Solution:

• Concepts:
  Lagrangian mechanics
• Reasoning:
  We are asked to find the Lagrangian and Hamiltonian of the system.
• Details of the calculation:
  d/dt(∂L/∂(dq/dt)) -  ∂L/∂q = 0.
  (a)  For q₁ = x we obtain d²y/dt² + ω₀² y = 0,
  and for q₂ = y we obtain d²x/dt² + ω₀² x = 0.
  The solutions are x = X₀exp(iω₀t) and y = Y₀exp(iω₀t), with X₀ and Y₀ complex constants that depend on the initial conditions,
  The problem is that of a two-dimensional, isotropic, harmonic oscillator.
  (b) 
  H(q, p, t) = ∑_i(dq_i/dt)p_i - L.   p_x = ∂L/∂(dx/dt) = mdy/dt,   p_y = ∂L/∂(dy/dt) = mdx/dt.
  H = p_xp_y/m + mω₀²xy.
  (c)  xy = ½((dx'/dt)² + (dy'/dt)²),  L = ½m((dx'/dt)² + (dy'/dt)² - ω₀²(x'² + y'²).
  Using these coordinates, we recognize the Lagrangian of a two-dimensional, isotropic,harmonic oscillator.
  Lagrange's equations are d²x'/dt² + ω₀² x' = 0,  d²y'/dt² + ω₀² y' = 0.
  Real solutions are x' = Ccos(ω₀t + Φ_x'),  y' = Dcos(ω₀t + Φ_y').
  C, D, Φ_x',  and Φ_y' depend on the initial conditions.
  p'_x= ∂L/∂(dx/'dt) = m dx'/dt,  p'_y= ∂L/∂(dy/'dt) = m dy'/dt, 
  H = (p'_x² + p'_y²)/(2m) + mω₀²(x'² + y'²)/2. 
  (d)  E = mω₀²(C² + D²)/2.

Problem:

Consider a simple plane pendulum consisting of a mass m attached to a string of length l.  After the pendulum is set into motion, the length of the string is shortened at a constant rate

dl/dt = -Θ = constant.

The suspension point remains fixed.  Consider only times for which l₀ - Θt > 0, i.e. for which the mass has not yet contacted the suspension point.
(a)  Compute the Lagrangian and write down Lagrange's equation of motion for small displacements from equilibrium.
(b)  Compute the Hamiltonian function.
(c)  Compare the Hamiltonian and the total energy and discuss the conservation of energy for this system.

Solution:

• Concepts:
  Lagrangian Mechanics
• Reasoning:
  We are asked to compute the Lagrangian and the Hamiltonian and find and solve Lagrange's equations.
• Details of the calculation:
  (a)  L = T - U.
  As long as (l₀ - Θt) > 1 we have
  T = ½m(l₀ - Θt)²(dθ/dt)² + ½mΘ²,  U = - mg(l₀ - Θt) cosθ.
  L = ½m(l₀ - Θt)²(dθ/dt)² + ½mΘ² + mg(l₀ - Θt)cosθ is the Lagrangian of the system.
  ∂L/∂(dθ/dt) = m(l₀ - Θt)²dθ/dt,  d/dt(∂L/∂(dθ/dt)) = m(l₀ - Θt)²d²θ/dt² - 2mΘ(l₀ - Θt)dθ/dt.
  ∂L/∂θ = -mg(l₀ - Θt)sinθ.
  (l₀ - Θt)d²θ/dt² - 2Θdθ/dt = -gsinθ is the equation of motion.
  For small angular displacement θ:  (l₀ - Θt)d²θ/dt² - 2Θdθ/dt = -gθ.
  
  (b)  H(p_θ, θ) = p_θ (dθ/dt) - L,  p_θ = ∂L/∂(dθ/dt) = m(l₀ - Θt)²dθ/dt,  H = p_θ²/(m(l₀ - Θt)²) - L
  H(p_θ, θ) = p_θ²/(2m(l₀ - Θt)²) - mg(l₀ - Θt)cosθ - ½mΘ² ≠ T + U.

  (c)  The constraints do explicitly depend on time, so H ≠ T + U, the total energy of the system. 
  H = H(t), H is not a constant of motion.
  The energy is not conserved. 
  dE/dt = p_θ²Θ/(m(l₀ - Θt)³) + mgΘcosθ = m(l₀ - Θt)(dθ/dt)²Θ + mgΘcosθ is the rate that work is done on the system.
  dE/dt = FΘ = where F is the tension in the string.  F = m(l₀ - Θt)(dθ/dt)² + mgcosθ.

Problem:

Consider the 2D problem of a free particle of mass m moving in the xy plane.
(a)  Use the Lagrangian formalism to find the equations of motion of the particle using Cartesian coordinates (x, y) in an inertial reference frame.
(b)  Now switch to explicitly time dependent coordinates.
X = xcos(ωt) + ysin(ωt),  Y = -xsin(ωt) + ycos(ωt). 
These would be the Cartesian coordinates of the particle in a reference frame rotating with constant angular speed ω counterclockwise about the z-axis of the inertial reference frame, i.e. ω = ωk.  Write down the Lagrangian in terms of the coordinate X and Y and the corresponding velocities.   Note:  x = Xcos(ωt) - Ysin(ωt),  y = Xsin(ωt) + Ycos(ωt).
(c)  Find the equations of motion in terms of the new coordinates.  Identify the fictitious forces appearing in the rotating frame.
(d)  What are the conditions for a circular orbit of radius R = (X² + Y²)^½ about the origin in the rotating frame?
(d)  Find the Hamiltonian H, and use Hamilton's equations to find the equations of motion.

Solution:

• Concepts:
  The Lagrangian formalism
• Reasoning:
  We are asked to use explicitly time-dependent coordinates.
• Details of the calculation:
  (a)  L = T = ½m(v_x² + v_y²), d/dt(∂L/∂v_i) = 0,  v_x = constant, v_y = constant.
  (b)  x = Xcos(ωt) - Ysin(ωt),  y = Xsin(ωt) + Ycos(ωt).
  v_x = v_X cos(ωt) - ω X sin(ωt) - v_Y sin(ωt) - ω Y cos(ωt).
  v_y = v_X sin(ωt) + ω X cos(ωt) + v_Y cos(ωt) - ω Y sin(ωt).
  v_x² + v_y² =  v_X² + v_Y² + ω²(X² + Y²) - 2ω(v_XY - v_YX)
  L = ½m(v_X² + v_Y² + ω²(X² + Y²) - 2ω(v_XY - v_YX))
  (c)  d/dt(∂L/∂v_X) - ∂L/∂X = 0, d/dt(∂L/∂v_Y) - ∂L/∂Y = 0.
  The equations of motions are a_X = ω²X + 2ω v_Y,  a_y = ω²Y - 2ω v_X, 
  mω²X and mω²Y  are the X- and Y-component of the centrifugal force, respectively.
  m2ω v_Y and - m2ω v_X  are the X-t and Y-component of the Coriolis force, respectively.
  (c)  Circular orbit: X² + Y² = R².  For a circular orbit of radius R we need
  d²X/dt² =  -ω²X, d²Y/dt² =  -ω²Y, 
  ω²X + 2ω v_Y = -ω²X,  v_Y = -ωX,
  ω²Y - 2ω v_X = -ω²Y,  v_X =  ωY.
  The angular velocity of the particle in the rotating frame must be ω = -ωk .
  (d)  H = P_X v_X + P_Y v_Y - L.  P_X = ∂L/∂v_X = mv_X - mωY,  P_Y = ∂L/∂v_Y = mv_Y + mωX,
  H = ½m(v_X² + v_Y² - ω²(X² + Y²)) = (P_X² + P_Y²)/(2m) + ω(P_XY - P_YX)
  ∂H/∂X = -dP_X/dt = -ωP_Y,  ∂H/∂Y = -dP_Y/dt = ωP_X. 
  ∂H/∂P_X = dX/dt = P_X/m + ωY ,  ∂H/∂ P_Y = dY/dt =   P_Y/m - ωX .
  a_X = (dP_X/dt)/m + ωdY/dt = ωP_Y/m + ωdY/dt = 2ωv_{Y +}  ω²X,
  a_Y = (dP_y/dt)/m - ωdX/dt = -ωP_X/m - ωdX/dt = - 2ωv_{X +}  ω²Y.
  The Hamiltonian H = (P_X² + P_Y²)/(2m) + ω(P_XY - P_YX) does not explicitly depend on time, so it is conserved.  Since the coordinates explicitly depend on time, the Hamiltonian is not equal to the total energy.

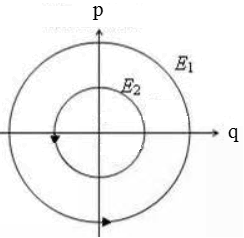
Problem:

Consider a system described by the Lagrangian L = ½mv² - ½kx², where v = dx/dt.
(a)  Express L in terms of the generalized coordinate q = (km)^¼x and the associated generalized velocity.
(b)  In terms of q and its canonical momentum p derive the form of the Hamiltonian H.  Is H a constant of motion?  Is it the energy E of the system?
(c)  Derive Hamilton's equations of motion and solve for q(t) and p(t).
(d)  Elaborate on the trajectories of the system in phase space.

Solution:

• Concepts:
  Lagrangian and Hamiltonian mechanic
• Reasoning:
  We are asked to choose a given generalized coordinate and the associated conjugate momentum.
• Details of the calculation:
  (a)  dq/dt = v_q = (km)^¼dx/dt,   L = (dq/dt)²/(2ω) - ωq²/2 = v_q²/(2ω) - ωq²/2 = L(q, v_q)
  (b)  p = dL/v_q = v_q/ω.
  H = pv_q - L = v_q²/(2ω) - ωq²/2 = (ω/2)(p² + q²) = H(p, q).
  H does not explicitly depend on time, so it is a constant of motion.
  The generalized coordinate and momentum do not explicitly depend on time, so H = E.
  (c)  Hamilton's equations are dp/dt = -∂H/∂q = -ωq,  dq/dt = p∂H/∂q = ωp.
  Solutions are q = A cos(ωt + Φ),  p = A sin(ωt + Φ),  A and Φ are determined by the initial conditions, ω = (k/m)^½.
  (d)  Trajectories in phase space are concentric circles about the origin (p = q = 0). 

  

  Phase-space points corresponding to different energies move on different circles.  All phase space points rotate ccw about the origin with the same angular speed ω.