Lagrangian problems, inclined planes
Problem:
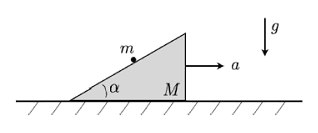
A wedge of mass M rests on a horizontal frictionless surface. A point mass m
is placed on the wedge, whose surface is also frictionless. Find the horizontal
acceleration a of the wedge.
Solution:
- Concepts:
Lagrangian Mechanics
- Reasoning:
All forces, except the forces of constraint, are derivable from a potential.
The Lagrangian formalism is well suited for such a system because we do not have
to solve for the forces of constraint or explicitly eliminate them from the
equations of motion.
- Details of the calculation:
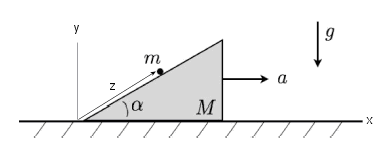
L = T - U.
T = Twedge + Tm = ½M(dx2/dt)2 +
½m[(dx1/dt)2 + (dy1/dt)2]. U =
mgy1.
Constraints: x1 = x2 + z cosα,
y1 = z sinα.
L = ½m[(dx2/dt)2 + (dz/dt)2 + 2(dx2/dt)(dz/dt)
cosα] + ½M(dx2/dt)2 - mgz sinα.
The equations of motion are obtained from
d/dt(∂L/∂(dq/dt)) - ∂L/∂q = 0.
for q1 = x2 and q2 = z.
(m + M)(d2x2/dt2) + m(d2z/dt2)
cosα = 0.
The horizontal position of the CM does not change.
m(d2z/dt2) + m(d2x2/dt2)cosα
+ mg sinα = 0.
Combining:
a = d2x2/dt2 = mg cosα sinα/(M + m -
m cos2α) = mg cosα sinα/(M + m sin2α).
You can also work from Newton's laws. The equations of motion then are
-Nsinα = m(d2x1/dt2) ,
Nsinα = M(d2x2/dt2),
-mg + Ncosα = m(d2y1/dt2),
with
x1 = x2 + z cosα, y1
= z sinα.
We have to solve for d2x2/dt2. Using
Newton's laws, we have to explicitly eliminate the force of constraint N.
From the first two equations:
m(d2x1/dt2) + M(d2x2/dt2)
= (m + M)(d2x2/dt2) + m(d2z/dt2)
cosα = 0.
From the third equation:
N = [m(d2z/dt2)sinα + mg]/cosα.
Insert this back into the second equation:
[m(d2z/dt2)sin2α + mgsinα]/cosα = M(d2x2/dt2).
[-(m + M)(d2x2/dt2)sin2α/cosα
+ mgsinα]/cosα = M(d2x2/dt2).
mg sinα cosα = M(d2x2/dt2)cos2α
+ (m + M)(d2x2/dt2)sin2α
mg sinα cosα = (d2x2/dt2) (M + m sin2α).
a = d2x2/dt2 = mg cosα sinα/(M + m sin2α).
Problem:
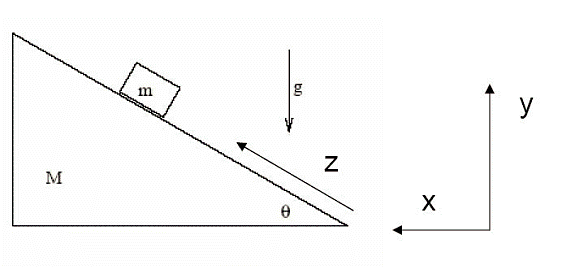
A wedge of mass M = 4.5 kg sits on a horizontal surface. Another mass m
= 2.3 kg sits on the sloping side of the wedge. The incline is at an angle θ =
31.7 degrees with respect to the horizontal, and g = 9.8 m/s. All surfaces are
frictionless. The mass m is released from rest on mass M, which is also
initially at rest. Use Lagrangian mechanics to determine the vector values of
the accelerations of both M and m once the mass is released.
Solution:
- Concepts:
Lagrangian Mechanics
- Reasoning:
We are asked to use Lagrangian Mechanics to solve the
problem.
- Details of the calculation:
L = T - U.
T = Twedge + Tm
= ½M(dx2/dt)2 + ½m[(dx1/dt)2 +
(dy1/dt)2]. U = mgy1.
Constraints: x1
= x2 + z cosθ, y1 = z sinθ.
L = ½ m[(dx2/dt)2
+ (dz/dt)2 + 2(dx2/dt)(dz/dt) cosθ] + ½M(dx2/dt)2
- mgz sinθ.
The equations of motion are obtained from
d/dt(∂L/∂(dq/dt)) -
∂L/∂q = 0,
for q = x2 and q = z.
(m + M)(d2x2/dt2)
+ m(d2z/dt2) cosθ = 0,
m(d2z/dt2)
+ m(d2x2/dt2) cosθ + mg sinθ = 0.
d2x2/dt2 = (mg cosθ sinθ)/(M + m - m cos2θ).
Inserting the numerical values we have:
d2x2/dt2
= 1.9624 m/s2,
d2z/dt2 = -6.82 m/s2,
d2x1/dt2 = -3.85 m/s2,
d2y1/dt2
= -3.58 m/s2.
Problem:
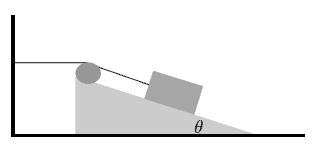
The system, shown in the diagram, consists of a wedge placed on a horizontal
surface and a block connected to a string that passes over a massless pulley
attached to the wedge. The other end of the string is attached to the wall so
that the string is horizontal between the wall and the pulley, and parallel to
the inclined surface between the pulley and the block. The wedge and the block
have equal masses m. The angle θ is given. When the system is released from
rest the block begins to slide along the inclined surface of the wedge.
Neglecting all friction, find the acceleration of the wedge.
Solution:
- Concepts:
Lagrangian mechanic
- Reasoning:
The Lagrangian method often simplifies the treatment of systems with
holonomic constraints.
- Details of the calculation:
Let the string have length L. Let x be the coordinate of the point
where the string touches the pulley.
Then coordinates of the point where the string attaches to the block are
x' = x + (L - x)cosθ, y' = h - (L - x)sinθ, where h is the height of the
point where the string attaches to the wall.
The kinetic energy of the system is T = ½ mvx2 + ½ m(vx'2
+ vy'2) = ½ m vx2 (3 - 2cosθ).
The potential energy is U = m g x sinθ + constant.
L = ½ m vx2 (3 - 2cosθ) - m g x sinθ
∂L/∂vx = mvx(3 - 2cosθ), d/dt(∂L/∂vx) = max(3
+ 2cosθ), ∂L/∂x = - m g sinθ.
ax = - g sinθ/(3 - 2cosθ).
Problem:
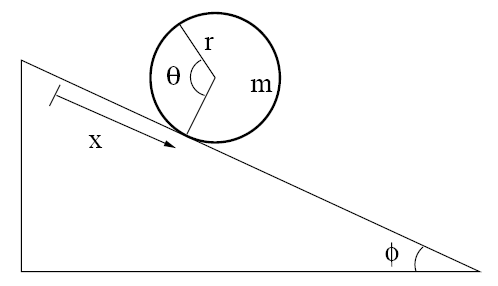
Consider a hoop of mass m and radius r rolling without slipping down an
incline.
(a) Determine the Lagrangian L(x, dx/dt) of this
one-degree-of-freedom system. Derive from it the Lagrange equation and its
solution for initial condition x0 = 0, dx/dt|0 = 0.
(b) Determine the alternative Lagrangian L(x, dx/dt, θ, dθ/dt) and
the holonomic constraint f(x, θ) = 0 that must accompany it. Derive the
associated three equations of motion for the two unknown dynamical variables x
and θ, and the undetermined Lagrange multiplier λ. Solve these equations
for the same initial conditions as in (a) and determine the static frictional
force of constraint between the hoop and the incline.
Solution:
- Concepts:
Lagrange's Equations, Lagrange multipliers
- Reasoning:
In part (a) we use the constraint of rolling to eliminate
the coordinate θ.
In part (b) we are asked to use the method of Lagrange
multipliers. Then the equations of motion are be obtained from
d/dt(∂L/∂(dqk/dt)) - ∂L/∂qk = ∑lλlalk,
Σk alk dqk + alt dt = 0.
- Details of the calculation:
(a) L = T - U.
T = (m/2)v2
+ (I/2)ω2. v = dx/dt, ω = dθ/dt = v/r, I = mr2, U =
-mgxsinΦ.
L = m(dx/dt)2 + mgxsinΦ.
∂L/∂v = 2mdx/dt,
(d/dt)∂L/∂v = 2md2x/dt2, ∂L/∂x = mgsinΦ.
d2x/dt2
= (g/2)sinΦ. ax = (g/2)sinΦ, vx = (gt/2)sinΦ, x = (gt2/4)sinΦ.
(b) L = (m/2)(dx/dt)2 + (mr2/2)(dθ/dt)2 +
mgxsinΦ.
Constraint: dθ = dx/r, dx - rdθ = 0.
We have two
coordinates, x and θ, and one equation of constraint, dx - rdθ = 0, which
must be cast into the form λ1∑a1k dqk = 0,
λ1(a1x dx + a1θ dθ) = 0.
Therefore a1x = 1, a1θ = -r.
∂L/∂v = mdx/dt,
(d/dt)∂L/∂v = md2x/dt2, ∂L/∂x = mgsinΦ.
∂L/∂ω = mr2dθ/dt,
(d/dt)∂L/∂ω = mr2d2θ/dt2, ∂L/∂θ = 0.
md2x/dt2
- mgsinΦ = λ, mr2d2θ/dt2 = -rλ, d2x/dt2
= rd2θ/dt2.
3 equations, 3 unknowns.
d2x/dt2
= (g/2)sinΦ, d2θ/dt2 = (g/(2r))sinΦ, λ = -(mg/2)sinΦ.
Here λ = Fx is the force of constraint associated with the
coordinate x. It is the static frictional force of constraint between
the hoop and the incline.
The generalized force of constraint associated with the coordinate θ is -rλ
= r(mg/2)sinΦ. It is the torque acting on the hoop, pointing into
the page.
Problem:
Two spheres are of the same radius R and mass M, but one is solid and the
other is a hollow shell (of negligible thickness). Both spheres roll
(without sliding) down a ramp of incline θ.
(a) Which sphere will have the
greater acceleration down the ramp?
(b) Determine the Lagrangian for the
motion of the sphere and derive the equation of motion for both cases.
Solution:
- Concepts:
Lagrange's Equations
- Reasoning:
All forces except the forces of constraint are derivable
from a potential. The Lagrangian formalism is well suited for such a
system. We are asked to derive Lagrange's equation of motion.
- Details of the calculation:
(a) We have a conservative system.
Potential energy is converted into rotational and translational kinetic
energy ½Iω2 + ½Mv2 with v = ωR. The moment of inertia
of the solid sphere I = (2/5)MR2 is smaller than the moment of
inertia of the thin spherical shell I = (2/3)MR2, so the solid
sphere will have the greater linear acceleration down the ramp.
(b) Set
up a coordinate system:
L = T - U. T = ½(I/R2 + M)(dx/dt)2, U =
Mgxsinθ.
L = ½(I/R2 + M)(dx/dt)2 - Mgxsinθ.
Equation of motion: (d/dt)(∂L/∂v) - ∂L/∂x = 0, with v = dx/dt.
(I/R2
+ M)d2x/dt2 + Mgsinθ = 0.
a = d2x/dt2
= (M/(I/R2 + M))gsinθ.
For the solid sphere: a = (5/7)
gsinθ.
For the spherical shell: a = (3/5) gsinθ.






