Lagrange multipliers

Problem:

A heavy particle with mass m is placed on top of a vertical hoop.  Calculate the reaction of the hoop on the particle by means of the Lagrange undetermined multipliers and Lagrange's equations.  Find the height at which the particle falls off.

Solution:

• Concepts:
  Lagrange's Equations, Lagrange multipliers
  d/dt(∂L/∂(dq_k/dt)) -  ∂L/∂q_k = ∑_lλ_la_lk,    Σ_k a_lk dq_k + a_lt dt =  0.
• Reasoning:
  The problem requires us to use the method of Lagrange multipliers. 
  
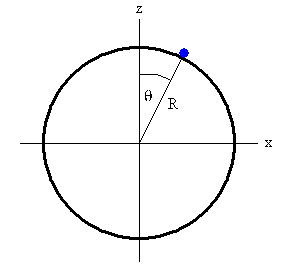
  Imagine the particle to be constrained to move on the hoop.  For a small θ, the force of constraint points away from the origin.  For a large θ it points toward the origin. The angle for which the force of constraint is zero is the angle at which the particle falls off.  To find the force of constraint as a function of θ, we use the technique of Lagrange multipliers.
  We have two coordinates, r and θ, and one equation of constraint, r = R, which must be cast into the form λ₁Σ a_1k dq_k = 0,  λ₁(a_1r dr + a_1θ dθ) = 0.
  The equation of constraint is r = R, dr  =  0,  therefore we can choose a_1r = 1, a_1θ  =  0.
• Details of the calculation:
  T = ½m((dr/dt)² + r²(dθ/dt)²),  U = mgr cosθ.
  L = ½m((dr/dt)² + r²(dθ/dt)²) - mgr cosθ.
  ∂L/∂(dr/dt)  = m dr/dt,  d/dt(∂L/∂(dr/dt)) = md²r/dt², 
  ∂L/∂r = mr(dθ/dt)² - mgcosθ.
  ∂L/∂(dθ/dt) = mr²(dθ/dt),  d/dt(∂L/∂(dθ/dt)) = mr²d²θ/dt² +  2mr(dθ/dt)(dr/dt),
  ∂L/∂θ = mgr sinθ.
  d/dt(∂L/∂(dr/dt)) - ∂L/∂r = λ₁a_1r,   
  md²r/dt² - mr(dθ/dt)² +  mgcosθ = λ₁                          (1)
  d/dt(∂L/∂(dθ/dt)) - ∂L/∂θ = λ₁a_1θ, 
  mr²d²θ/dt² +  2mr(dθ/dt)(dr/dt) - mgr sinθ = 0.             (2)
  
  The equation of constraint is dr = 0.  We have three equations and three unknowns,
  r(t), θ(t), and λ₁.
  dr/dt = 0 --> d²r/dt² = 0, r = R.
  mR²d²θ/dt² - mgRsinθ = 0.                                             (from 2)
  -mR(dθ/dt)² +  mgcosθ = λ₁,                                           (from 1)
  dθ/dt =  [(g/R)cosθ - λ₁/(mR)]^½.                                  
  The particle falls off when λ₁ = 0.   Then  dθ/dt =  [(g/R)cosθ]^½.
  
  To find an expression for λ₁ we need to solve the differential equation
  d²θ/dt² = (g/R)sinθ
  for dθ/dt and equate the solution with dθ/dt =  [(g/R)cosθ - λ₁/(mR)]^½. 
  Denote dθ/dt = f(θ).
  df(θ)/dt = [df(θ)/dθ]f(θ) = ½df²(θ)/dθ = (g/R)sinθ.
  f²(θ) = A - (2g/R)cosθ.
  dθ/dt =  [A - (2g/R)cosθ]^½.
  
  Initial conditions:  dθ/dt = 0 for θ = 0, A = 2g/R.
  dθ/dt =  [(2g/R) - (2g/R)cosθ]^½.
  The particle falls off when (g/R)cosθ  = (2g/R) - (2g/R)cosθ, or cosθ = (2/3), θ = 48.19^o.
  
  To find λ₁ set (2g/R) - (2g/R)cosθ = (g/R)cosθ - λ₁/(mR).
  λ₁/(mR) = (3g/R)cosθ - (2g/R), λ₁ = 3mg cosθ - 2mg.
  λ₁a_1r = F_r, F_r =  is the reaction of the hoop on the particle.

Problem:

A bead of mass m slides without friction on a circular loop of radius a.  The loop lies in a vertical plane.

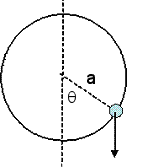
(a)  Use the Lagrange multiplier method and find the appropriate Lagrangian including terms expressing the constraints. 
(b)  Apply the Euler-Lagrange equations to obtain the equations of motion and solve for θ << 1.
(c)  Find the force of constraint.

Solution:

• Concepts:
  Lagrangian Mechanics, Lagrange multipliers
• Reasoning:
  We are instructed to use the Lagrange multiplier method
• Details of the calculation:
  T = ½m((dr/dt)² + r²(dθ/dt)²),  U = -mgrcosθ,  L = T - U.
  (a)  We have two coordinates, r, and θ, and one equation of constraint, r = a, which we want to cast into the form λ₁∑ a_1k dq_k = 0.  We have dr = 0, a_1r = 1, a_1θ = 0.
  (b)  Equations of motion:
  d/dt(∂L/∂(dq_k/dt)) -  ∂L/∂q_k = ∑_lλ_la_lk,    Σ_k a_lk dq_k + a_lt dt =  0.
  d²r/dt² - r(dθ/dt)² - gcosθ = λ₁/m.
  d²θ/dt² =  -(g/r)sinθ.
  The equation of constraint is r = a, dr/dt = d²r/dt² = 0.
  Therefore d²θ/dt² =  -(g/a)sinθ,  -a(dθ/dt)² - gcosθ = λ₁/m.
  If θ << 1, then d²θ/dt² = -(g/a)θ.  θ = θ_maxsin(ωt + θ₀),  ω² = g/a.
  -a(dθ/dt)² - g = λ₁/m,  λ₁ = -mg + ma(dθ/dt)² = -mg - mv²/a.
  (c)  The force of constraint has magnitude mg + mv²/a and points radially inward towards the origin.

Problem:

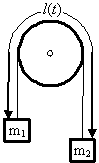
Two masses m₁ and m₂ are connected by a massless string that runs over a frictionless pulley.  The length of the string, l, somehow increases at a constant rate, i.e. l(t) = l₀ + l₁t.  Use the method of Lagrange multipliers to determine the tension of the string at time t.

Solution:

• Concepts:
  Lagrange's Equations, Lagrange multipliers
  d/dt(∂L/∂(dq_k/dt)) -  ∂L/∂q_k = ∑_lλ_la_lk,    Σ_k a_lk dq_k + a_lt dt =  0.
• Reasoning:
  The problem requires us to use the method of Lagrange multipliers. 
  Let the generalized coordinate x_i denote the distance along the string from the top of the pulley to the mass m_i.
  Then L = m₁(dx₁/dt)²/2 + m₂(dx₂/dt)²/2 + m₁gx₁ + m₂gx₂.
  The equation of constraint is x₁ + x₂ = l₀ + l₁t,  dx₁ + dx₂ - l₁dt = 0.  There is only one equation of constraint.  We write λ(a_x1 dx₁ + a_x2 dx₂ + a_tdt)  = 0.
  a_x1 = 1,  a_x2 = 1,  a_t = -l₁.
• Details of the calculations:
  The equations of motion are
  m₁d²x₁/dt² - m₁g = λ,
  m₂d²x₂/dt² - m₂g = λ.
  From dx₁ + dx₂ - l₁dt = 0 we obtain
  d²x₁/dt² + d²x₂/dt² = 0.
  Solving these 3 equations we obtain
  m₁d²x₁/dt² - m₂d²x₂/dt² = (m₁ - m₂)g .
  m₁d²x₁/dt² + m₂d²x₁/dt² = (m₁ - m₂)g .
  d²x₁/dt² = (m₁ - m₂)g/(m₁ + m₂).
  λ = m₁(m₁ - m₂)g/(m₁ + m₂) - m₁g = -2m₁m₂g/(m₁ + m₂).
  λ is the force of constraint acting on m₁, its magnitude is the tension in the string, the - sign indicates that it is acting upward on m₁.

Problem:

Consider a particle of mass m constrained to remain on the surface of a cylinder of radius b.   Let the axis of the cylinder be the z-axis.  The particle is subject to the force of gravity mg in the negative z-direction. 
(a)  Use the Lagrange multiplier method and find the appropriate Lagrangian including a term expressing the constraint. 
(b)  Apply the Euler-Lagrange equations to obtain the equations of motion. 
(c)  Find the force of constraint and briefly discuss why this value is reasonable and to be expected.
(d)  Now, repeat parts (a) and (b) without using the Lagrange multiplier method.  Instead, build the constraint into the general coordinates.

Solution:

• Concepts:
  Lagrangian Mechanics, Lagrange multipliers
• Reasoning:
  We are asked to find the force of constraint using Lagrange multipliers.
• Details of the calculation:
  T = ½m((dr/dt)² + (dz/dt)²) +  ½mr²(dφ/dt)²,  U = -mgz,  L = T - U.
  (a)  We have three coordinates, r, z, and φ, and one equation of constraint, r = b, which we want to cast into the form λ₁∑ a_1k dq_k = 0.  We have dr = 0, a_1r = 1, a_1z = a_1ɸ = 0.
  (b)  Equations of motion:
  d/dt(∂L/∂(dq_k/dt)) -  ∂L/∂q_k = ∑_lλ_la_lk,    Σ_k a_lk dq_k + a_lt dt =  0.
  md²r/dt² - mr(dφ/dt)² = λ₁,  md²z/dt² + mg = 0,  mr²d²φ/dt² + 2mr(dr/dt)(dφ/dt) = 0
  The equation of constraint is r = b, dr/dt = d²r/dt² = 0.
  Therefore d²z/dt² = -g,  z(t) = z₀ + v_z0t - ½ gt²,
  d²φ/dt² = 0,  φ(t) = φ₀ + ω₀t, with ω₀ = dφ/dt,
  mbω₀² = -λ₁.
  (c)  The force of constraint has magnitude mbω₀² and points radially inward towards the z-axis.  It is the centripetal force providing the centripetal acceleration mv_φ²/b.
  (d)  T = ½m(dz/dt)² +  ½mb²(dφ/dt)²,  U = -mgz,  L = T - U.
  d/dt(∂L/∂(dq_k/dt)) -  ∂L/∂q_k = 0.
  md²z/dt² + mg = 0,  mr²d²φ/dt² = 0.
  d²z/dt² = -g,  z(t) = z₀ + v_z0t - ½ gt².
  d²φ/dt² = 0,  φ(t) = φ₀ + ω₀t.