Standard Lagrangian problems (other problems)

One generalized coordinate

Problem:

Consider the system shown below, in which two bodies of the same mass M are connected by a massless string across a massless frictionless pulley.  The coefficient of friction for the mass on the incline is μ and the angle of the incline is 30^o with respect to the horizontal.  Define the z-coordinate as shown.  Assume downward motion and μ < 1.
(a)  Determine the Lagrangian L(z, dz/dt) for the system.
(b)  If at t = 0, z = z₀, and v = v₀, find z(t) until the block is stopped by the pulley.

Solution:

• Concepts:
  Lagrange's equations,  d/dt(∂L/∂(dq/dt)) -  ∂L/∂q = Q_j.
  where L contains the potential of the conservative forces and Q_j represents the generalized forces not arising from a potential.
• Reasoning:
  In this problem conservative and non-conservative forces (gravity and friction) are present.
• Details of the calculation:
  (a)  We only need one generalized coordinate.
  Assume downward motion.  Then
  T = M(dz/dt)², U = Mgz + Mgzsin(30^o) + constant = 1.5 Mgz + constant.  L = T - U.
  Q_z = μMgcos(30^o).
  (b)  Lagrange's equation yields 2Md²z/dt² + 1.5Mg =  μMgcos(30^o).
  d²z/dt² = (μcos(30^o) - 1.5)g/2 = g'.
  Since μ < 1, g' is negative.
  dz/dt = -v₀ - |g'|t,  z(t) = z₀ - v₀t - ½|g'|t², until the block is stopped by the pulley.

Problem:

A flexible uniform string of mass M and length L slides smoothly over a circular, frictionless peg of radius R, with the right-hand end moving downward in a uniform gravitational field with g = 9.8 m/s².  The string is released from rest in a situation where the right-hand end hangs below the left-hand end by an amount d.

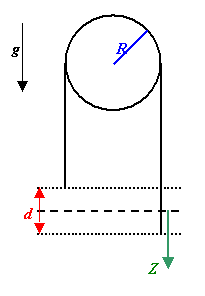
(a)  Find an expression for Z, the vertical position of the right-hand end as a function of time during the interval when the string is still in contact with the peg over the full upper half of the peg.  Assume that the position Z of the right-hand end is measured downward from the equilibrium position Z = 0.
(b)  In the limit R --> 0, find Z also for times subsequent to the loss of contact with the peg.

Solution:

• Concepts:
  Newton's second law or Lagrange's equations.
• Reasoning:
  For a conservative system we find and solve the equations of motion.
• Details of the calculation:
  (a)  F(z') = (M/L)g2z'.  U = -∫₀^z F(z')dz'.
  T = ½M(dz/dt)²,  U  = -Mgz²/L
  L = T - U,  d²z/dt² = 2gz/L
  z(t) = Bexp(At) + B'exp(-At) is the general solution.
  A = (2g/L)^½, B an B' are determined by the initial conditions.
  z(0) = B + B' = d/2, dz/dt|₀ = A(B - B') = 0,  B = B' = d/4.
  z(t) = (d/2)cosh(At) = (d/2)cosh((2g/L)^½t),
  (b)  When R => 0 the result from (a) is valid for z < L/2. 
  For z > L/2 we have a freely falling object, falling from an initial position z = L/2 with initial velocity v_c = v(L/2).
  From energy conservation we have ½M(dz/dt)² - Mgz²/L = -Mgd²/4L.
  Evaluating at z = L/2 we find
  v_c = v(L/2) = [g(L²-d²)/2L]^½ = [(gL - d²/L)/2]^½
  at t_c = t(L/2) = (L/(2g))^½cosh^-1(L/d).
  z(t) = (L/2) + v_c(t - t_c) + ½g(t - t_c)².

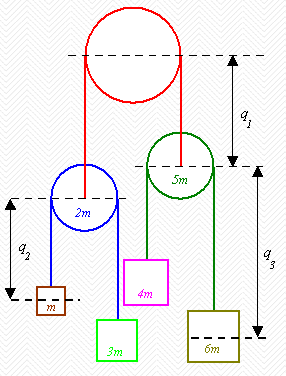
Problem:

For the Atwood Machine shown, all pulleys are smooth and non-rotating and all cords are inextensible.  Work out the accelerations of 3m and 5m.

Solution:

• Concepts:
  Lagrange's Equations
• Reasoning:
  All forces except the forces of constraint are derivable from a potential.  The Lagrangian formalism is well suited for such a system.
• Details of the calculation:
  Let the y-axis point downward.  Let l₁ be the hanging portion (not the part in contact with the pulley) of the length of the red string, l₂ the hanging portion of the length of the blue string, and l₃ the hanging portion of the length of the green string.  Let us find the kinetic and potential energy of the masses in terms of the generalized coordinates q₁, q₂, and q₃.  We can then write down the Lagrangian and the equations of motion, which will yield the accelerations of the masses.
   

  mass	y-coordinate	vecocity	T	U
  2m	l1-q1	-dq1/dt	m(dq1/dt)2	-2mg[l1-q1]
  m	l1-q1+q2	-dq1/dt+dq2/dt	(m/2)[(dq1/dt)2+(dq2/dt)2-2(dq1/dt)(dq2/dt)]	-mg[l1-q1+q2]
  3m	l1-q1+l2-q2	-dq1/dt-dq2/dt	(3m/2)[(dq1/dt)2+(dq2/dt)2+2(dq1/dt)(dq2/dt)]	-3mg[l1-q1+l2-q2]
  5m	q1	dq1/dt	(5/2)m(dq1/dt)2	-5mg[q1]
  4m	q1+l3-q3	dq1/dt-dq3/dt	2m[(dq1/dt)2+(dq3/dt)2-2(dq1/dt)(dq3/dt)]	-4mg[q1+l3-q3]
  6m	q1+q3	dq1/dt+dq3/dt	3m[(dq1/dt)2+(dq3/dt)2+2(dq1/dt)(dq3/dt)]	-6mg[q1+q3]

  T = (21m/2)(dq₁/dt)²+2m(dq₂/dt)²+5m(dq₃/dt)²+2m(dq₁/dt)(dq₂/dt)+2m(dq₁/dt)(dq₃/dt).
  U = -mg(9q₁-2q₂+2q₃+constant).
  L = T - U.
  d/dt(∂L/∂(dq/dt)) -  ∂L/∂q = 0.
  Using q₁ we find:  21d²q₁/dt² + 2d²q₂/dt² + 2d²q₃/dt² - 9g = 0.
  Using q₂ we find:  4d²q₂/dt² + 2d²q₁/dt² + 2g = 0.
  Using q₃ we find:  10d²q₃/dt² + 2d²q₁/dt² - 2g = 0.
  Solving the 3 equations for the 3 unknowns d²q₁/dt², d²q₂/dt², and d²q₃/dt² we find
  d²q₁/dt² = 24g/49,  d²q₂/dt² = -73g/49,  d²q₃/dt² = 5g/49.
  Therefore
  a(3m) = -d²q₁/dt²-d²q₂/dt² = -29g/49,
  a(5m) = d²q₁/dt² = 24g/49.

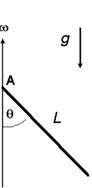
Problem:

A thin uniform rod of length L and rotates with a constant angular velocity ω around a fixed point A.  (See figure!)   Find the angle of inclination θ.

Solution:

• Concepts:
  Lagrangian Mechanics or Motion in a non-inertial frame
• Reasoning:
  In the inertial frame we have motion with constraints. In the rotating frame the rod is at rest.
• Details of the calculation:
  Lagrangian Mechanics:
  T = ½(mL²/3)d²θ/dt² + ½∫₀^Lρdl (l sinθ ω)², U = -(mgL/2)cosθ
  T = ½(mL²/3)d²θ/dt² + ½ mL² sin²θ ω²/3, U = -(mgL/2)cosθ
  Lagrange's equation:  (mL²/3)d²θ/dt² + (mL² sinθ cosθ/3)ω² - (mgL/2)sinθ = 0.
  For d²θ/dt² = 0 we need cosθ = 3g/(2Lω²).
  
  Motion in a non-inertial frame:
  In a frame rotating with angular frequency ω the total torque is zero.
  The torque is produce by the gravitational force and by the fictitious centrifugal force ρdl lsinθ ω² acting on each element of the rod with mass dm = ρdl.
  Total torque about point A:
  τ = -mg(L/2)sinθ + ∫₀^Lρdl (ω²lsinθ) lcosθ.
  τ = 0 --> (mgL/2)sinθ = ∫₀^Lρdl l² ω² sinθ cosθ = mL² sinθ cosθ ω²/3.
  cosθ = 3g/(2Lω²),
  θ = cos^-1(3g/(2Lω²)).

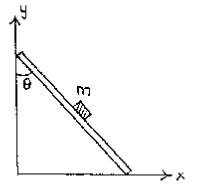
Problem:

A particle of mass m is attached (so it cannot slide) to the midpoint of a weightless rod of length l.  The ends of the rod are constrained to move along the x and y axes.  A uniform gravitational field acts
in the negative y-direction.  Use θ as a generalized coordinate.  Neglect friction.
(a)  Write the Lagrangian and obtain the equation of motion.
(b)  Solve the equation of motion for small θ, i.e. |θ| << 1, assuming that, at t = 0, θ = θ₀ and dθ/dt = 0.

Solution:

• Concepts:
  Lagrange's Equations
• Reasoning:
  All forces except the forces of constraint are derivable from a potential.  The Lagrangian formalism is well suited for such a system.  We are asked to write down and solve Lagrange's equation of motion.
• Details of the calculation:
  (a)  As long as the rod remains in contact with the wall, we have the constraints
  x = (l/2)sinθ  and  y = (l/2)cosθ  for the coordinates of m.
  The Lagrangian L is given by L = T - U.
  T = ½m ((dx/dt)² + (dy/dt)²),  U = mg(l/2)cosθ.
  dx/dt = (l/2)cosθ dθ/dt,  dy/dt = -(l/2)sinθ dθ/dt,  T = (1/8)ml²(dθ/dt)².
  L = (1/8)ml²(dθ/dt)² - mg(l/2)cosθ.
  We need only one generalized coordinate and one generalized velocity.
  d/dt(∂L/∂(dq/dt)) -  ∂L/∂q = 0.
  Lagrange's equation yields ¼ml²d²θ/dt² = (mglsinθ)/2.
  (b) Let θ << 1, then sinθ  ≈ θ and d²θ/dt²  ≈ (2g/l)θ. 
  The general solution to this differential equation is
  θ = A exp((2g/l)^½t) + B exp((2g/l)^½t).
  The initial conditions are θ(0) = θ₀,  dθ/dt|_t=0 = 0.
  Therefore A + B = θ₀,  A - B = 0, A = B = θ₀/2.
  θ = (θ₀/2) exp((2g/l)^½t) + (θ₀/2)  exp((2g/l)^½t) = θ₀ cosh((2g/l)^½t).
  This solution is only valid as long as θ is still small.

Problem:

A particle of mass m moves in one dimension acted upon by the force
F(x) = -kx + a/x³
where k and a are both positive constants. 
(a) Sketch the potential energy. 
(b) Sketch the velocity phase space portrait for this system.
(c) Calculate the locations of the equilibrium points of the motion.
(d) Indicate whether each of these points is stable or unstable.
(e) Find the Hamiltonian.

Solution:

• Concepts:
  Phase space portraits, Lagrangian mechanics
• Reasoning:
  We are asked to sketch the phase space portrait and write down the Hamiltonian.
• Details of the calculation:
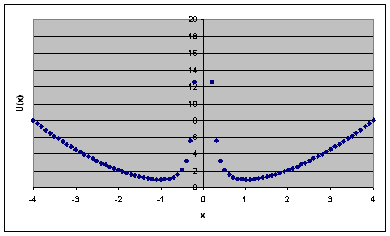
  (a)  F(x) = -dU(x)/dx.  U(x) = ½ kx² + a/(2x²).
  The sketch shows U(x) for a = k = 1.
  
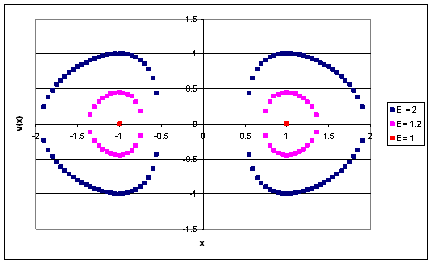
  (b) Velocity phase portrait:
  F(x) = 0 at x = ±(a/k)^¼, where U(x) = U_min = ½(ka)^½ + ½(ak)^½ = (ak)^½.
  For the system we have E ≥ (ak)^½.
  Energy conservation: E = ½mv(x)² + U(x).  v(x) = ±(2(E - U(x))/m )^½.
  
  (c)  The equilibrium points are x = ±(a/k)^¼.  The potential energy goes to infinity at x = 0 and that point cannot be reached for any motion.
  (d)  Both points are stable.
  (e)  H = p²/(2m) + ½ kx² + a/(2x²).

Multiple generalized coordinates

Problem:

(a)  Give the definition of a cyclic variable.
(b)  How is it related to conservation laws and physical symmetry?
(c)  Give two examples of systems described by Lagrangians with cyclic variables and relate them to part b.

Solution:

• Concepts:
  The Lagrangian, the Hamiltonian, conservation laws, cyclic variables
• Reasoning:
  The problem asks for the definition of a cyclic variable and its relationship to conservation laws.
• Details of the calculation:
  (a)  The Lagrangian is a function of the generalized coordinates and velocities and time.  Any generalized coordinate, which does not appear explicitly in the Lagrangian, is said to be cyclic.
  ∂L/∂q_i = 0 implies q_i = cyclic.
  (b)  The corresponding generalized momentum p_i = ∂L/∂(dq_i/dt) is a constant of motion, it is conserved.  A coordinate which is cyclic in the Lagrangian is also cyclic in the Hamiltonian.  The connection between the symmetry properties of the physical system and constants of motion can be derived in terms of the Hamiltonian.
  Example:  H is symmetric about an axis.  H is invariant under rotation about this axis, it does not depend on the angle of rotation about this axis.  The angle is a cyclic coordinate, the corresponding angular momentum is conserved.
  (i)  A particle in a central potential:
  L = ½m((dr/dt)² + r²(dФ/dt)²) - U(r).
  L_Ф = mr² dФ/dt is constant.
  (ii)  A particle subject to a constant force F = F₀k:
  L = ½m((dx/dt)² + (dy/dt)² + (dy/dt)²) + Fz.
  x and y are cyclic, p_x = m dx/dt and p_y = m dy/dt are constants of motion.

Problem:

Consider the 2D problem of a free particle of mass m moving in the xy plane.
(a)  Use the Lagrangian formalism to find the equations of motion of the particle in polar coordinates (r, θ).
(b)  Find the general solution for the orbit r(t).
Hint:  Use energy conservation!
(c)  At t = 0, let r = b,  θ = 0,  dr/dt = 0,  dθ /dt = ω₀.  Find r(t) and θ(t).

Solution:

• Concepts:
  Lagrangian mechanics
• Reasoning:
  We are instructed to use the Lagrangian formalism to find the equations of motion of a free particle in  polar coordinates (r, θ).
• Details of the calculation:
  (a)  Let v_r = dr/dt,  ω = dθ/dt.
  x = r cosθ, y = r sinθ,  v_x = -r sinθ ω + v_rcosθ,  v_y = r cosθ ω + v_r sinθ
  v_x² + v_y² = v_r² + r² ω².
  L = T = ½m(v_x² + v_y²) = ½m(v_r² + r² ω²)
  d/dt(∂L/∂v_r) - ∂L/∂r = 0,  d/dt(∂L/∂ω) - ∂L/∂θ = 0.
  Equation of motion for θ:
  m r² dθ/dt = M = constant.  Angular momentum is conserved.
  Equation of motion for r:
  md²r/dt² = m r ω².
  d²r/dt² = M²/(m²r³).
  (b)  E = ½m(v_r² + r² ω²) = ½mv_r² + M²/(2mr²)
  dr/dt = ((2/m)(E - M²/(2mr²))^½.
  ∫dr/((2/m)(E - M²/(2mr²))^½ = ∫dt
  t - t₀ = (m/2)∫dr²/(2mEr² - M²)^½ = [(m/2E)(r² - M²/(2mE))]^½.
  r = [2E(t - t₀)²/m + M²/(2mE))]^½.
  (c)  M = mb²ω₀,  E = ½ mb²ω₀²,   r² = b²(ω₀²(t - t₀)² + 1) , r²(t = 0) = b² --> t₀ = 0.
  r(t) = b(ω₀²t² + 1)^½,  dθ(t)/dt = b²ω₀t/[ b²(ω₀²t² + 1)],   θ(t) = tan^-1(ω₀t) or θ(t)
  x =  r cosθ = r/secθ = r/(tan²θ + 1)^½ = r/(ω₀²t² + 1)^½ = b.
  y =  r sinθ = r/cosecθ = r/(cot²θ + 1)^½ = r/(1/ω₀²t² + 1)^½ = bω₀t = vt.