Lagrangian problems, oscillations

Problem:

A light (assume massless) rod of length r is fixed at the origin, and a mass M is attached to the other end, as shown. 

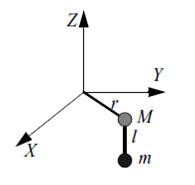
The rod is constrained to move in the XY-plane.  A pendulum of length l and mass m attached to M can oscillate in the YZ-plane.  Use θ for the angle of the rod in the XY-plane, and Φ for the angle of the pendulum in the YZ-plane.
(a) Find Lagrange's equations for the system of the rod and pendulum in terms of θ and Φ.
(b) Find the normal frequencies and normal modes of vibration for small oscillations.

Solution:

• Concepts:
  Lagrangian mechanics, L = T - U
• Reasoning:
  We are asked to find the Lagrangian and solve the resulting equations of motions for small oscillations.
• Details of the calculation:
  TM = ½Mr²(dθ/dt)²,  T_m = ½m((dx/dt)² + (dy/dt)² + (dz/dt)²).
  x = r cosθ, y = r sin θ + l sinΦ, z = -l cosΦ.
  dx/dt = -r sinθ dθ/dt,  dy/dt = r cosθ dθ/dt + l cosΦ dΦ/dt,
  dz/dt = + l sinsΦ dΦ/dt,
  T_m = ½m(r²(dθ/dt)² + l²(dΦ/dt)² + 2rl cosθ (dθ/dt) cosΦ (dΦ/dt).
  U = -mgl cosΦ
  L = ½(M + m)r²(dθ/dt)² + ½ml²(dΦ/dt)² + mrl cosθ cosΦ (dθ/dt)(dΦ/dt) + mgl cosΦ
  ∂L/∂(dθ/dt) = (M + m)r²(dθ/dt) + mrl cosθ cosΦ (dΦ/dt)
  d/dt ∂L/∂(dθ/dt) = (M + m)r²d²θ/dt² - mrl[sinθ cosΦ (dΦ/dt)(dθ/dt) + cosθ sinΦ (dΦ/dt)² - cosθ cosΦ d²Φ/dt²].
  ∂L/∂θ = -mrl sinθ cosΦ (dθ/dt)(dΦ/dt).
  
  ∂L/∂(dΦ/dt) = ml²(dΦ/dt) + mrl cosθ cosΦ (dθ/dt)
  d/dt(∂L/∂(dΦ/dt)) = ml²d²Φ/dt² - mrl[sinθ cosΦ (dθ/dt)² + cosθ sinΦ (dΦ/dt)(dθ/dt)  - cosθ cosΦ d²θ/dt²].
  ∂L/∂Φ = -mrl cosθ sinΦ (dθ/dt)(dΦ/dt) - mgl sinΦ.
  Equations of motion:
  (M + m)r²d²θ/dt² - mrl[cosθ sinΦ (dΦ/dt)² - cosθ cosΦ d²Φ/dt²] = 0.
  d²Φ/dt² - (r/l)[sinθ cosΦ (dθ/dt)² - cosθ cosΦ d²θ/dt²] + (g/l) sinΦ = 0.
  
  (b)  In the small angle approximation (θ << 1, Φ << 1) we have the equations of motion
  (M + m)r²d²θ/dt² + mrl d²Φ/dt² = 0.
  d²Φ/dt² + (r/l)d²θ/dt² + (g/l)Φ = 0.
  Assume Φ = Φ₀ exp(iωt),  θ = θ₀ exp(iωt) for a normal mode.  Then
  ω²(M + m)r²θ₀ + ω²mrlΦ₀ = 0,  ω²(Φ₀ + (r/l)θ₀) - (g/l)Φ₀ = 0.
  There is only one oscillatory solution with ω not equal to zero.
  θ₀ = -(m/(m + M))(l/r)Φ₀,  ω² = ((m + M)/M)(g/l).

Problem:

A simple pendulum of length l (massless string) and mass m is suspended from a pivot point on the circumference of a thin massless disc of radius a that rotates with a constant angular velocity ω about its central axis as shown in the figure.  Find the equation of motion of the mass m in terms of the generalized variable θ.

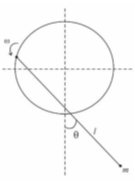
Solution:

• Concepts:
  Lagrangian Mechanics
• Reasoning:
  All forces except the forces of constraint are derivable from a potential.  The Lagrangian formalism is well suited for such a system.
• Details of the calculation:
  The coordinates of the pivot point are X = a cosωt,  Y = a sinωt.
  The coordinates of the mass m are x = X + l sinθ, y = Y - l cosθ.
  dx/dt = -aω sinωt + l cosθ dθ/dt,  dy/dt = aω cosωt + l sinθ dθ/dt.
  T = ½m((dx/dt)² + (dy/dt)²)
  = ½m[a²ω² + l²(dθ/dt)² + 2aωl(dθ/dt)(-sinωt cosθ + cosωt sinθ)]
  = ½m[a²ω² + l²(dθ/dt)² + 2aωl(dθ/dt) sin(θ - ωt)].
  U = mgy = mg(a sinωt - l cosθ).
  L = T - U. 
  Equation of motion:  d/dt ∂L/∂(dθ/dt) - ∂L/∂θ = 0.
  ∂L/∂(dθ/dt) = ml²(dθ/dt)+ maωl sin(θ - ωt).
  d/dt(∂L/∂(dθ/dt)) = ml²d²θ/dt² + maωl cos(θ - ωt)(dθ/dt - ω).
  ∂L/∂θ = maωl (dθ/dt)cos(θ - ωt) - mgl sinθ.
  ml²d²θ/dt² + maωl cos(θ - ωt)(dθ/dt - ω) - maωl (dθ/dt)cos(θ - ωt) + mgl sinθ = 0.
  
  d²θ/dt² - (a/l)ω²cos(θ - ωt) + (g/l)sinθ = 0
  is the equation of motion.

Problem:

Consider the pendulum illustrated in the figure with l the length of the string, m the mass of the ball, F_g the gravitational force, and Φ the angular displacement.  (You may assume the string to be of fixed length and negligible mass).  Use Lagrange's equation to derive an equation of motion that neglects terms of order Φ³ and higher.

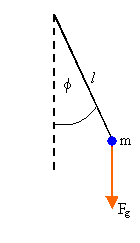
Solution:

• Concepts:
  Lagrange's Equations
• Reasoning:
  All forces except the forces of constraint are derivable from a potential.  The Lagrangian formalism is well suited for such a system.  We are asked to find the equation of motion.
• Details of the calculation:
  T = ½ m l²(dΦ/dt)²,  U = -mglcos(Φ),  L = T - U.
  We have one generalized coordinate, Φ, and one generalized velocity, dΦ/dt.
  d/dt(∂L/∂(dq/dt)) -  ∂L/∂q = 0.
  The equation of motion therefore is ml²dΦ²/dt² + mglsin(Φ) = 0,
  or dΦ²/dt² + (g/l)sin(Φ) = 0.
  sinΦ = Φ - Φ³/3! + ...
  Neglecting terms of order Φ³ and higher we have dΦ²/dt² + (g/l)Φ = 0.

Problem:

A simple pendulum of length with a bob of mass m is attached to a massless support moving horizontally with constant acceleration a. 
(a)  Compute the Lagrangian function.
(b)  Write down Lagrange's equation of motion. 
(c)  Simplify and compare the equation of motion to that for a simple pendulum with a fixed (motionless) support.

Solution:

• Concepts:
  Lagrange's equations
• Reasoning:
  We are asked to obtain Lagrange's equation of motion.
• Details of the calculation:
  (a)  L = T - U.
  T = ½m((dx/t)² +(dy/dt)²).
  x = ½at² + sinθ,  y = -b cosθ.
  dx/dt = at + cosθ(dθ/dt),  dy/dt = sinθ(dθ/dt).
  T = ½m(b²(dθ/dt)² + a²t² + 2at cosθ(dθ/dt)).
  U = mgy = -mg cosθ.
  L = ½m(b² (dθ/dt)² + a²t² + 2at cosθ (dθ/dt)) + mg cosθ.
  (b)  ∂L/∂ (dθ/dt) = mb² (dθ/dt) + mat bcosθ,  d/dt(∂L/∂ (dθ/dt)) = mb²d²θ/dt² - mat bsinθ (dθ/dt) + ma bcosθ, 
  ∂L/∂θ = -matbsinθ (dθ/dt) - mg bsinθ.
  bd²θ/dt² + g sinθ + a cosθ = 0.
  (c)  sin(θ + θ₀) = sinθ cosθ₀ + cosθ sinθ₀.
  Let g sinθ = c sinθ cosθ₀, and a cosθ = c cosθ sinθ₀.
  Then g  = c cosθ₀, and a = c sinθ₀,  c = (g² + a²)^½,  tanθ₀ = a/g.
  Define φ = θ + θ₀.  Then the equation of motion becomes
  bdφ²/dt² = -c sinφ.  This equation becomes bdθ²/dt² = -g sinθ when a = 0.
  For a simple pendulum we have bdθ²/dt² = -g sinθ.

Problem:

A point particle of mass m slides without friction along a hoop of radius R and mass M.  The hoop rolls without slipping along a horizontal surface.  What is the frequency of small oscillations of the point mass, when it is close to the bottom of the hoop?

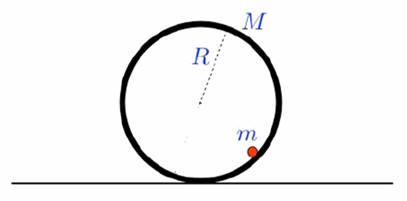
Solution:

• Concepts:
  Lagrangian mechanics
• Reasoning:
  All forces except the forces of constraint are derivable from a potential.  The Lagrangian formalism is well suited for such a system.
• Details of the calculation:
  Let θ be the angle through which the hoop rotates and Φ be the angle the line from the center of the hoop to the particle makes with the vertical as shown below.
  For the hoop X = Rθ.  For the point mass x = Rθ + R sinΦ, y = -R cosΦ.

  

  T = ½(MR²(dθ/dt)² + I(dθ/dt)²) +  ½m[R(dθ/dt) + R (dΦ/dt) cosΦ]² + ½m[R (dΦ/dt) sinΦ]²
  = (M + ½m)R²(dθ/dt)² + ½mR²(dΦ/dt)² + mR²cosΦ(dθ/dt)(dΦ/dt).
  U = - mgR cosΦ.
  L = T - U.
  ∂L/∂(dθ/dt) = 2(M + ½m)R²(dθ/dt)+ mR²cosΦ(dΦ/dt) = constant, because (dθ/dt) is cyclic.
  ∂L/∂θ = 0.
  In the small angle approximation we then have
  (2M + m)d²θ/dt² + md²Φ/dt² = 0.
  d²θ/dt² = -[m/(2M + m)]d²Φ/dt².
  
  In the small angle approximation we keep only terms to second order in the small quantities in the Lagrangian or terms to first order in the small quantities in the equations of motion.
  L =  (M + ½m)R²(dθ/dt)² + ½mR²(dΦ/dt)² + mR²(dθ/dt)(dΦ/dt) - mgRΦ²/2.
  ∂L/∂(dΦ/dt) = mR²(dΦ/dt) + mR²(dθ/dt).
  d/dt(∂L/∂(dΦ/dt)) = mR²d²Φ/dt² + mR²d²θ/dt².
  ∂L/∂Φ = -mgRΦ.
  mR²d²Φ/dt² + mR²d²θ/dt² + mgRΦ = 0.
  d²Φ/dt² + d²θ/dt² + (g/R)Φ = 0.

  d²Φ/dt² -[m/(2M + m)]d²Φ/dt² + (g/R)Φ = 0.
  [2M/(2M + m)]d²Φ/dt² = -(g/R)Φ.
  d²Φ/dt² = -ω²Φ
  ω² = (g/R)(2M + m)/(2M).

Problem:

A thin rod of linear density ρ and length L is balanced on a cylindrical arc of radius R as shown.

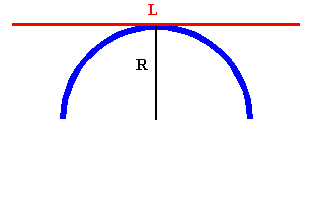
If one end of the rod is tapped, find the frequency of small oscillations for the rod.

Solution:

• Concepts:
  The Lagrangian formalism, small oscillations
• Reasoning:
  We are asked to find the frequency of small oscillations.
• Details of the calculation:
  Assume we have a very thin rod.
  
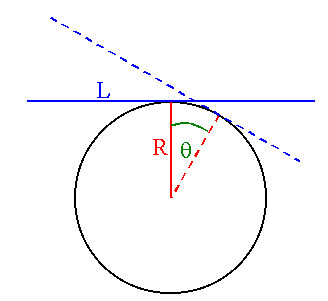
  L = T - U.
• T = ½M((dX/dt)² + (dY/dt)²) + ½I(dθ/dt)².
  U = MgY.
  X and Y are the coordinates of the CM.
  Let the origin of the coordinate system be the center of the circle in the figure above.
  X = R sinθ - Rθ cosθ.
  Y = R cosθ + Rθ sinθ.
  Small angle approximation:  In L, keep only terms up to second order in θ.
  X = Rθ - Rθ = 0.
  Y = R(1 - θ²/2) + Rθ² = R(1 + θ²/2).
  dX/dt = 0, dY/dt = Rθ dθ/dt.
  Therefore
  L = ½MR²θ²(dθ/dt)² + ½M(L²/12)(dθ/dt)² - MgR(1 + θ²/2)
  ≈ ½M(L²/12)(dθ/dt)² - Mg R(1 + θ²/2).
  Again:  In the small angle approximation, where we only keep terms to second order in the small quantities.
  The equation of motion is 
  d²θ/dt² = -(12gR/L²)θ,
  which yields ω = (12gR/L²)^½, independent of the mass of the rod.

Problem:

Consider an Atwood machine with a massless pulley and two masses, m and M, which are attached at opposite ends to a string of fixed length that is hung over the pulley.  For this Atwood machine the center of the pulley is supported by a spring of spring constant k.
(a)  Find the Lagrangian and the resulting equations of motion.
(b)  Find the equilibrium position of the pulley and its frequency of oscillation.  Consider your result in the limit m = M and discuss.

Solution:

• Concepts:
  Small oscillation, Lagrangian mechanics.
• Reasoning
  We are asked to find the Lagrangian and the equations of motion.
• Details of the calculation:
  (a)  Assume that the center of the pulley is a distance z measured in the downward direction from the equilibrium length of the spring.  Assume that the distance from the center of the pulley for M is x measured in the downward direction.  For m the distance from the center of the pulley downward is L - x, where L is a constant related to the length of the string.
  The kinetic energy of the two masses is
  T = ½M(dz/dt + dx/dt)² + ½m(dz/dt - dx/dt)².
  The potential energy of the two masses and the spring is
  U = -Mg(z + x) - mg(z - x) + ½kZ².
  The Lagrangian is
  L = ½M(dz/dt + dx/dt)² + ½m(dz/dt - dx/dt)²  + Mg(z + x) + mg(z - x) - ½kz^{2
  =} ½M((dz/dt⁾²+ (dx/dt)² + 2(dz/dt)(dx/dt)) + ½m((dz/dt⁾²+ (dx/dt)² - 2(dz/dt)(dx/dt))
  + Mg(z + x) + mg(z - x) - ½kz².
  The x-equation of motion is
  (M - m)g = (M + m)d²x/dt² + (M - m)d²z/dt².
  The z-equation of motion is
  (M + m)g - kz = (M + m)d²z/dt² + (M - m)d²x/dt².
  (b)  Solving for d²x/dt² from the x-equation:
  d²x/dt² = (g - d²z/dt²)(M - m)/(M + m).
  Substituting into the z-equation:
  (M + m)g - kz = (M + m)d²z/dt² + (M - m)²(g - d²z/dt²)/(M + m).
  [(M + m)² - (M - m)²]d²z/dt² = (M + m)²g - (M + m)kz - (M - m)²g.
  4Mm d²z/dt² = 4Mmg - (M + m)kz.
  d²z/dt² = g - ((M + m)/(4Mm))kz.
  The equilibrium position z₀ of the center of the pulley requires d²z/dt² = 0.  Therefore
  z₀ = (g/k) 4Mm/(M + m).
  Let z' = z - z₀.  Then d²z'/dt² = - ((M + m)/(4Mm))kz'.
  z' = Cexp(iωt)
  The frequency of oscillation is
  ω² = k(M + m)/(4Mm) = k/(4μ). where μ = Mm/(M + m).
  In the limit m = M the frequency of oscillation reduces to ω² = k/(2m), which is what you expect since neither mass is accelerating due to gravity.