Coupled oscillations, other systems

Problem:

A rigid uniform bar of mass M and length L is supported in equilibrium in a horizontal position by two massless springs attached at each end.  The identical springs have spring constant k.  The motion of the center of mass is constrained to move parallel to the vertical x-axis.  Furthermore, the motion of the bar is constrained to lie in the xz plane.  Let x₁ and x₂ be the departures of the two ends from their equilibrium positions, as shown.

(a)  Show that the moment of inertia for a bar about the y-axis through its center of mass is ML²/12.
(b)  Construct the Lagrangian for the bar-spring arrangement assuming only small deviations from equilibrium.
(c)  Calculate the vibrational frequencies of the normal modes for small amplitude oscillations.
(d)  Describe the normal modes of oscillations.

Solution:

• Concepts:
  Small oscillations, coupled oscillations, normal modes
• Reasoning:
  L = ½∑_ij[T_ij(dq_i/dt)(dq_j/dt) - k_ijq_iq_j]  with T_ij = T_ji,  k_ij = k_ji. 
  Solutions of the form q_j = Re(A_je^iωt) can be found.  We can find the ω² from det(k_ij - ω²T_ij) = 0.
• Details of the calculation:
  (a)  Put the origin of the coordinate system at the CM.
  I = ∫r² dm with dm with dm = (M/L)z. 
  I = 2∫₀^L/2 z² (M/L) dz =2(M/L)[z³/3]₀^L/2 = ML²/12.
  
  (b)  L = K_tr + K_rot - U.   Let x₁ and x₂ be the displacements from equilibrium.
  K_tr = ½M(dx_CM/dt)² = (1/8)M(dx₁/dt + dx₂/dt)².
  K_rot = ½I(dθ/dt)² =½(ML²/12)[(dx₁/dt - dx₂/dt)/L]² = (½4)M(dx₁/dt - dx₂/dt)².
  We use the small angle approximation, sinθ = θ = (x₂ - x₁)/L,  cosθ = 1 - θ²/2.
  We have elastic and gravitational potential energy. 
  U_sp = ½k(x₁ - x₀)² + ½k(x₂ - x₀) ²,  U_g = ½Mg(x₁ + x₂).
  U = ½kx₁² +½kx₂² + kx₀²  - kx₀x₁ - kx₀x₂ + ½Mgx₁ + ½Mgx₂.
  Since kx₀ = ½Mg we can write U = ½kx₁² + ½kx₂², and 
  L = (1/6)M[(dx₁/dt)² + (dx₂/dt)²] + (1/6)M(dx₁/dt)(dx₂/dt) - ½kx₁² - ½kx₂².
  
  (c)  We can write
  L = ½∑_ij[T_ij(dq_i/dt)(dq_j/dt) - k_ijq_iq_j]  with T_ij = T_ji,  k_ij = k_ji. 
  Here T₁₁ = T₂₂ = M/3, T₁₂ = T₂₁ = M/6,  k₁₁ = k₂₂ = k,  k₁₂ = k₂₁ = 0.
  Solutions of the form q_j = Re(A_je^iωt) can be found.  We need
  det(k_ij-ω²T_ij) = 0.

  
  
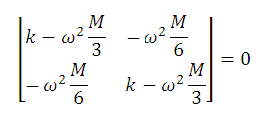
  ω² = 4k/M ± 2k/M,  ω_- = (2k/M)^½,  ω₊ = (6k/M)^½. 
  (d)  The normal mode corresponding to ω_- has the bar moving up and down while remaining horizontal.  That corresponding to ω₊ has the center of mass of the bar remain stationary while the two ends oscillate up and down exactly out of phase.

Problem:

A uniform horizontal rectangular plate (mass M, length L, width W) rests with its corners on four similar vertical springs with spring constant k.  Find the normal modes of vibration and prove that their frequencies are in the ratio 1 : √3 : √3.
Solution:

• Concepts:
  Small oscillations, normal modes
• Reasoning:
  We are asked to find the 3 normal modes of the plate. 
  
  Assume that the CM of the plate is restricted to move along a vertical line.
  The symmetry of the setup implies that the three normal modes are:
  (a)  The plate moves up and down and does not rotate.
  (b)  The plate rotates about the line x₂, the CM is fixed.
  (c)  The plate rotates about the line x₁, The CM is fixed.
• Details of the calculation:
  (a)  T = ½M(dz/dt)².  Here z is the displacement from its equilibrium position in the gravitational field.
  U = ½4kz²,  d²z/dt² = -4(k/m)z,  ω_a² = 4k/M.
  (b)  T = ½I_b(dθ/dt)²,  θ = 2z/L for small oscillations.  U = ½4k(L²/4)θ².
  I_b = 2W∫₀^L/2ρ(x)x²dx = 2Wρ(x)(L/2)³/3 = 2W(M/(LW))(L/2)³/3 = ML²/12.
  I_b = ML²/12.
  d²θ/dt² = -12 (k/m)θ,  ω_b² = 12(k/m),  ω_b = (3)^½ω_a.
  (c)  T = ½I_c(dΦ/dt)²,  Φ = 2z/W for small oscillations.  U = ½4k(W²/4)Φ².
  I_c = MW²/12.
  d²Φ/dt² = -12 (k/m)Φ,  ω_c² = 12(k/m),  ω_c = (3)^½ω_a.

Problem:

Phonons are quantized lattice vibrations, and many aspects of these excitations can be understood in terms of simple mode counting.
(a)  Estimate the number of phonon modes in 1 cm³ of a crystalline material with an inter-atomic spacing of 2 Angstrom.
(b)  Assuming that in thermal equilibrium each phonon mode has k_BT of energy, give a numerical estimate of the heat capacity ΔE/ΔT of this 1 cm³ of material, in [J/K].

Solution:

• Concepts:
  Normal modes of coupled oscillators
• Reasoning:
  We are asked to estimate the number of normal modes of a large number of coupled harmonic oscillators.
• Details of the calculation:
  (a) We have N atoms, N coupled oscillators.  We therefore have 3N normal modes.  (We may want to neglect translation and rotation of the crystal as a whole, but since N is so large, it does not make any difference.)
  N = n³, n = 10^-2m/(2*10^-10m) = 5*10⁷.  N = 1.25*10²³.
  (b)  k_B = 1.380658 * 10^-23 J/K.
  E = 3Nk_BT,  ΔE/ΔT = 3Nk_B = 5.19 J/K  for the 1 cm³ piece of material.
  This is a reasonable number.  For water the specific heat is 4.186 J/(g K).

Problem:

A naive model of a solid is that of a bunch of balls (atoms) connected by springs (bound by inter-atomic potentials which can be approximated by harmonic potentials near equilibrium).  If each inter-atomic spring has spring constant k, you can relate this microscopic value to the macroscopically measurable value of Young's modulus, Y.  Young's modulus is the ratio of stress (F/A, or applied force, F, perpendicular to the cross-sectional area, A, of a bar of material per unit cross-sectional area), to strain (ΔL/L, or the fractional change in length of the bar of material); thus, Y = (F/A)/(ΔL/L).  Evaluate k for the inter-atomic springs of aluminum, which has a Young's modulus of 70 GPa.  Assume that the aluminum atoms are arranged in a simple cubic lattice (they are really face-centered cubic); you can determine the inter-atomic spacing by knowing that the density of aluminum is 2.70 g/cm³ and that a mole of aluminum has a mass of 27 g.  Express your result for k in SI units.

 Solution:

• Concepts:
  Hooke's law, general physics
• Reasoning:
  We are asked to use general physics principles to evaluate a simple model of a solid.
• Details of the calculation:
  Assume we have N atoms in a cube of volume 1 m³.   Let n = N/m³.  Then we have N^(2/3) atoms on each 1 m² surface.  Assume each atom is acted of by a force f perpendicular to the surface and pointing outward, f = (F/A)/n^(2/3).  Each spring in a chain of atoms perpendicular to the surface is stretched by an amount x = f/k, the change in length of the chain is ΔL/L = n^(1/3)f/k.
  Therefore Y = fn^(2/3)/( n^(1/3)f/k) = kn^(1/3)
  n = (2.7 g/cm³)*(10⁶ cm³/m³)*(6.02*10²³ atoms/mole)*1 mole/27 g) = 6.02*10²⁸ atoms/m³.
  k = (70*10⁹/3.92*10⁹) N/m  = 17.9 N/m.
  (This yields a reasonable vibrational frequency of ω = (k/m)^½ = 2*10¹³/s for out of phase motion.)

Problem:

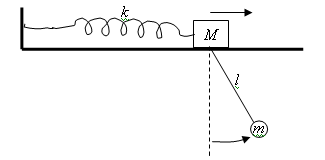
A pendulum consisting of a mass m and a weightless string of length l is mounted on a mass M, which in turn slides on a support without friction and is attached to a horizontal spring with force constant k, as seen in the diagram.  There is a slot in the support in order that the pendulum may swing freely.
(a)  Set up Lagrange's equations.
(b)  Find the normal mode frequencies for small oscillations. What are those frequencies to zeroth order in m/M, when  m << M?

Solution:

• Concepts:
  Lagrangian Mechanics, coupled oscillations
• Reasoning:
  We are asked to write down and solve Lagrange's equations.
• Details of the calculation:
  (a) T = ½M(dX/dt)² + ½m[(dx/dt)² + (dy/dt)²],  x = X + ℓ sinθ, y = -ℓcosθ.
  T = ½M(dX/dt)² + ½m[(dX/dt)² + ℓ²(dθ/dt)² + 2(dX/dt)(dθ/dt)ℓcosθ].
  U = -mgℓcosθ + ½kX². 
  L = T - U = ½(M + m)(dX/dt)² + ½m[ℓ²(dθ/dt)² + 2(dX/dt)(dθ/dt)ℓcosθ] + mgℓcosθ - ½kX². 
  We have two generalized coordinates, X and θ.  Lagrange's equations are
  d/dt ∂L/∂(dX/dt) - ∂L/∂X = 0,  d/dt ∂L/∂(dθ/dt) - ∂L/∂θ = 0.
  1st equation:  (M + m)d²X/dt² + md²θ/dt²ℓcosθ - m(dθ/dt)²ℓsinθ = -kX.
  2nd equation: ℓ²d²θ/dt² + d²X/dt²ℓcosθ = -gℓ sinθ.

  (b)  Assume X and θ are small quantities, and in the equations of motion keep only terms to first order in small quantities.  Then we have, using sinθ ~ θ, cosθ ~ 1.
  1st equation:  (M + m)d²X/dt² + mℓd²θ/dt²  = -kX.
  2nd equation: d²θ/dt² + (1/ℓ)d²X/dt²  = -(g/ℓ)θ.
  We obtain the same equations if we make the small displacements approximation earlier and keep only terms up to second order in the Lagrangian.
  Try solutions X = Aexp(iωt),  θ = (B/ℓ)exp(iωt),  then
  -ω²(M + m)A - ω²mB = -kA,  -ω²B - ω²A = -(g/ℓ)B.
  We solve this system of equations by setting  

  
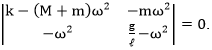
  ω⁴ - ω²(k/M + (g/ℓ)(1 + m/M)) + kg/(ℓM) = 0.
  ω² = (k/M + (g/ℓ)(1 + m/M))/2 ± ½((k/M + (g/ℓ)(1 + m/M))² - 4kg/(ℓM))^½.
  ω₊² = (k/M + (g/ℓ)(1 + m/M))/2 + ½((k/M + (g/ℓ)(1 + m/M))² - 4kg/(ℓM))^½.
  ω_-² = (k/M + (g/ℓ)(1 + m/M))/2 - ½((k/M + (g/ℓ)(1 + m/M))² - 4kg/(ℓM))^½.
  The frequencies for small oscillations are ω₊ and ω_-.
  [For the relative displacements we have B =  Aω²/((g/l) - ω²).  ω₊² > g/l,  so A and B have opposite signs for this mode.]
  
  As m --> 0, ω₊ --> (k/M)^½, ω_- = (g/ℓ)^½.  The modes effectively decouple.  The small mass m does no longer influence the motion of the big mass M.  When M oscillates with frequency (k/M)^½, m becomes a driven harmonic oscillator without damping (for small oscillations).  The most general solution is a superposition of oscillations with the driving frequency and oscillations with the natural frequency of the oscillator.