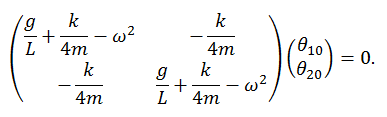Coupled oscillations, pendula

Problem:

A pendulum is composed of two masses, 3m and m, and two strings of equal length L as shown.  

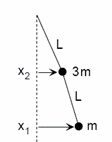
At t = 0 the system is released from rest with the upper (heavier) mass not displaced from its equilibrium position and the lower mass displaced to the right a distance a.
x₂(0) = 0, x₁(0) = a << L.
Find an expression for the subsequent motion of the lower mass, x₁(t).

Solution

• Concepts:
  Small, coupled oscillations; normal modes
  L = ½∑_ij[T_ij(dq_i/dt)(dq_j/dt) - k_ijq_iq_j]  with T_ij = T_ji,  k_ij = k_ji. 
  Solutions of the form q_j = Re(A_je^iωt) can be found.  We can find the ω² from det(k_ij - ω²T_ij) = 0.
• Reasoning:
  We are asked to find the motion of the masses for small displacements.
• Details of the calculations:
  Let Φ₁ and Φ₂ be the generalized coordinates.  Then
  x₂ = LsinΦ₂, x₁ = L(sinΦ₁ + sinΦ₂),
  y₂ = LcosΦ₂, y₁ = L(cosΦ₁ + cosΦ₂).
  For small displacements we have sinΦ = Φ, cosΦ = 1 - Φ²/2.
  The kinetic energy of the system is
  T = (3/2)m[(dx₂/dt)² + (dy₂/dt)²] + ½m[(dx₁/dt)² + (dy₁/dt)²]
  Let us only keep terms up to second order in Φ and dΦ/dt.  Then
  (dx₂/dt)² + (dy₂/dt)² = L²(dΦ₂/dt)²,
  (dx₁/dt)² + (dy₁/dt)² = L²[(dΦ₂/dt)² + (dΦ₁/dt)² + 2(dΦ₁/dt)(dΦ₂/dt)].
  T = (3/2)mL²(dΦ₂/dt)² + ½mL²[(dΦ₂/dt)² +(dΦ₁/dt)² + 2(dΦ₁/dt)(dΦ₂/dt)].
  The potential energy of the system is
  U = -mgy₁ - 3mgy₂  = (mgL/2)(Φ₁² + 4Φ₂²) + constant.
  We have:
  T = ½∑_ij T_ij(dΦ_i/dt)(dΦ_j/dt),   U = ½∑_ij k_ijΦ_iΦ_j.
  T₁₁ = mL²,  T₂₂ = 4mL², T₁₂ = T₂₁ = mL²,
  k₁₁ = mgL, k₂₂ = 4mgL, k_ij(i ≠ j) = 0.
  
  .
   
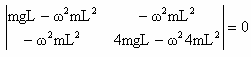  ω² = (g/L)(8 ± 4)/6, ω_a² = 2(g/L), ω_b² = (2/3)(g/L).
  Φ_i = A_iexp(iω_αt)
  For mode a:  A₂ = -A₁/2
  For mode b:  A₂ = A₁/2
  
  Most general motion for a system starting from rest:
  Φ₁ = Aexp(iω_at) + Bexp(iω_bt),  Φ₂ = -(A/2)exp(iω_at) + (B/2)exp(iω_bt).
  with A and B complex constants.
  
  x₁ = L(Φ₁ + Φ₂),  x₂ = LΦ₂.
  x₁ = L(|A|/2)cos(ω_at + φ_a) + L(3|B|/2)cos(ω_bt + φ_b), 
  x₂ = -L(|A|/2)cos(ω_at + φ_a) + L(|B|/2)cos(ω_bt + φ_b).,
  or
  x₁ = A'cos(ω_at + φ_a) + 3B'cos(ω_bt + φ_b), 
  x₂ = -A'cos(ω_at + φ_a) + B'cos(ω_bt + φ_b),
  with A' and B' real constants.
  
  dx₂/dt = -ω_aA'sin(ω_at + φ_a) - ω_b3B'sin(ω_bt + φ_b),
  dx₁/dt = ω_aA'sin(ω_at + φ_a) - ω_bB'sin(ω_bt + φ_b).
  
  Initial conditions:  x₁(0) = A'cos(φ_a) + 3B'cos(φ_b) = a,   x₂(0) = -A'cos(φ_a) + B'cos(φ_b) = 0. 
  -->  A'cos(φ_a) = B'cos(φ_b) = a/4.
  
  v₁(0) = -ω_aA'sin(φ_a) - ω_b3B'sin(φ_b) = 0,  v₂(0) = ω_aA'sin(φ_a) - ω_bB'sin(φ_b) = 0.
  --> sin(φ_a) = sin(φ_b) = 0,  cos(φ_a) = cos(φ_b) = 1, A' = B' = a/4.
  
  Subsequent motion of the lower mass:
  x₁(t) = (a/4)cos ω_at + (3a/4)cos ω_bt.

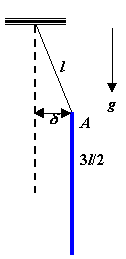
Problem:

A uniform thin rod of length 3l/2 and mass m is supported at one end A by a weightless string of length l under the gravitational force near the earth surface.
(a)  Calculate the normal modes and normal frequencies of small oscillations for motion in a vertical plane.
(b)  Now the end point A is slowly displaces by a small amount δ, (without gaining any kinetic energy.)  The system is then released from rest and allowed to move freely.  What is the subsequent motion?

Solution:

• Concepts:
  Small oscillations:  
  L = ½∑_ij[T_ij(dq_i/dt)(dq_j/dt) - k_ijq_iq_j]  with T_ij = T_ji,  k_ij = k_ji. 
  Solutions of the form q_j = Re(A_je^iωt) can be found.
  For a particular frequency ω_α we solve
  ∑_j[k_ij - ω_α²T_ij]A_jα = 0
  to find the A_jα.  The most generαl solution for eαch coordinαte q_j is α sum of simple hαrmonic oscillαtions in αll of the frequencies ω_α.
  q_j = Re∑_α(C_αA_jαexp(iω_αt)).
• Reasoning:
  We are asked to find the normal modes for small displacements.
• Details of the calculations:
  
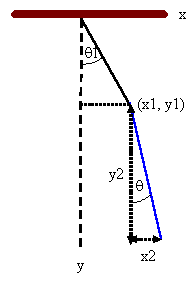
  (a)  The position of the CM of the rod is X = x₁ + x₂/2, Y = y₁ + y₂/2.
  For the rod we have:
  T = ½m[(dx₁/dt + ½ dx₂/dt)² + (dy₁/dt + ½ dy₂/dt)²]  + ½I(dθ/dt)².
  T is the kinetic energy of the motion of the CM and the motion about the CM.
  U = -mg(y₁ + y₂/2) + constant.
  For small oscillations x₁ = lsinθ₁ ~lθ₁, x₂ = (3/2)lsinθ ~ (3/2)lθ.
  y₁ = lcosθ₁ ~ l(1 - θ₁²/2), y₂ = (3/2)lcosθ ~ (3/2)l(1 - θ²/2).
  To second order in the small quantities we have:
  T = ½ml²((dθ₁/dt)²+¾²(dθ/dt)²+(3/2)(dθ₁/dt)(dθ/dt)+½(3/16)ml²(dθ/dt)²)
  = ½ml²((dθ₁/dt)²+¾(dθ/dt)²+(3/2)(dθ₁/dt)(dθ/dt))
  = ½∑T_ijq_iq_j.
  q₁ = θ₁, q₂ = θ, T₁₁ = ml², T₂₂ = ¾ml², T₁₂ = T₂₁ = ¾ml².
  U = mgl[(q₁²/2) +¾l(q₂²/2)] = ½∑k_ijq_iq_j.
  k₁₁ = mgl, k₂₂ = ¾mgl, k₁₂ = k₂₁ = 0.
  
  .
  
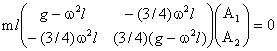  We have a solution if
  
  .
  
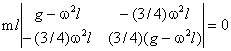  ¾(g-ω²l)² -(9/16)ω⁴l² = 0,  ω⁴ - 8(g/l)ω² + 4g²/l = 0.
  ω² = [4 ± (12)^½]g/l.
  mode 1:  ω₁² = [4 + (12)^½]g/l.
  (g - [4 + (12)^½]g)A₁ - ¾[4 + (12)^½]gA₂ = 0.  A₁ = -0.866 A₂.
  mode 2:  ω₂² = [4 - (12)^½]g/l.
  (g - [4 - (12)^½]g)A₁ - ¾[4 - (12)^½]gA₂ = 0.  A₁ = 0.866 A₂.
  
  (b)  The most general solution is q_j = Re∑_α(C_αA_jαexp(iω_αt)).
  θ₁ = Re(c₁exp(iω₁t) + c₂exp(iω₂t)),  θ = (1/0.866)Re(-c₁exp(iω₁t) + c₂exp(iω₂t)).
  Initial conditions:
  θ₁(0) = δ/l,  θ(0) = 0,  dθ₁/dt = dθ/dt = 0 at t = 0.
  Re(c₁ + c₂) = δ/l,  Re(c₁ - c₂) = 0,  Re(c₁) = Re(c₂) = δ/(2l).
  Re(iω₁c₁ + iωc₂) = 0,  Re(-iω₁c₁ + iωc₂) = 0.
  Im(ω₁c₁ + ωc₂) = 0,  Im(ω₁c₁ - ωc₂) = 0,  Im(c₁) = Im(c₂) = 0.
  θ₁(t) = (δ/(2l))[cosω₁t + cosω₂t],  θ(t) = (δ/(2*0.866*l))[cosω₁t - cosω₂t].

Problem:

Two pendula, each of which consists of a weightless rigid rod length of L and a mass m, are connected at their midpoints by a spring with spring constant k.  Consider only small displacements from equilibrium.

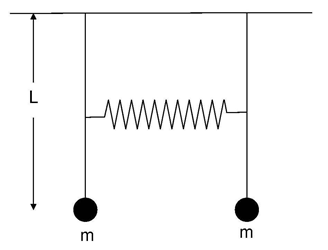
(a)  What are the frequencies of the normal modes of this system?  Briefly describe these modes.
(b)  At t = 0 the right pendulum is displaced by an angle θ to the right while the left pendulum remains vertical.  Both pendula are released from rest.  Describe the subsequent motion. 

Solution:

• Concept:
  Coupled small oscillations
• Reasoning:
  We are asked to solve for the motion of two coupled pendula.
• Details of the calculation:
  (a)  Call the left pendulum 1 and the right pendulum 2.  Let θ_i denote a small angular displacement of pendulum i to the right.
  Small angle approximation:  sinθ = θ, cosθ = 1 in the equations of motion.
  Define x₁ = Lθ_½,  x₂ = Lθ₂/2
  τ₁ = Iα₁ = mL²d²θ₁/dt² = -mgLθ₁ - kL²(θ₁ - θ₂)/4
  τ₂ = Iα₂ = mL²d²θ₂/dt² = -mgLθ₂ - kL²(θ₂ - θ₂)/4
  Equations of motion:
  d²θ₁/dt² = -(g/L)θ₁ - (k/m)(θ₁ - θ₂)/4
  d²θ₂/dt² = -(g/L)θ₂ - (k/m)(θ₂ - θ₁)/4
  Try solutions of the form θ_i = θ_i0 exp(iωt).  Then
  
  

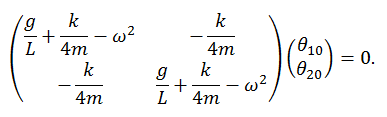
  Solve for ω by setting the determinant of the matrix equal to zero.
  ω² = (g/L + k/(4m)) ± k/(4m).
  
  ω₁² = g/L,  θ₁₀ = θ₂₀,  the pendula oscillate in phase.
  ω₂² = g/L + k/(2m),   θ₁₀ = -θ₂₀, the pendula oscillate 180^o out of phase.
  

  (b)  Most general solution: 
  θ₁(t) = Re(C₁exp(iω₁t) + C₂exp(iω₂t))
  θ₂(t) = Re(C₁exp(iω₁t) - C₂expi(ω₂t))
  dθ₁(t)/dt = Re(iω₁C₁exp(iω₁t) + iω₂C₂exp(iω₂t))
  dθ₂(t)/dt = Re(iω₁C₁exp(iω₁t) - iω₂C₂expi(ω₂t))
  Initial conditions at t = 0:
  Re(C₁ + C₂) = 0,   Re(C₁ - C₂) = θ₂₀,  Re(C₁) = - Re(C₂) = θ₂₀/2.
  Im(ω₁C₁+ ω₂C₂) = 0, Im(ω₁C₁+ ω₂C₂),  Im(C₁) = Im(C₂) = 0.

  θ₁(t) = (θ₂₀/2)(cos(ω₁t) - cos(ω₂t))
  θ₂(t) = (θ₂₀/2)(cos(ω₁t) + cos(ω₂t))
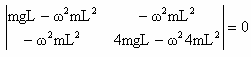
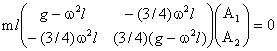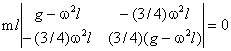