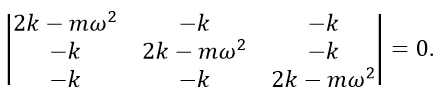Coupled oscillations, point masses and spring
Problem:
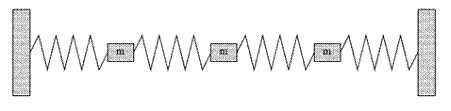
Find the eigenfrequencies and describe the normal modes for
a system of three equal masses m and four springs, all with spring constant k,
with the system fixed at the ends as shown in the figure below. The motion
can only take place in one dimension, along the axes of the springs.
Solution:
- Concepts:
Coupled oscillations, normal modes
- Reasoning:
We are asked to find the normal modes of coupled harmonic
oscillators.
- Details of the calculation:
The kinetic energy is T = ½[m(dx1/dt)2
+ m(dx2/dt)2 + m(dx3/dt)2],
and the potential energy is U = (k/2)[(x2 - x1)2
+ (x3 - x2)2 + x12 +
x32].
U = (k/2)[2x12 + 2x22
+ 2x32 - x1x2 - x2x1
- x2x3 - x3x2].
The xi
are the displacements from the equilibrium positions. We use the xi
as our generalized coordinates qi.
The Lagrangian is L = T -
U. This can be put into the form
L = ½∑ij[Tij(dqi/dt)(dqj/dt) - kijqiqj]
with Tij = Tji, kij = kji.
Here T11
= T 22 = T33 = m, Tij(i≠j) = 0,
k11
= k22 = k33 = 2k, k12 = k21 = k23
= k32 = -k, k13 = k31 = 0.
Solutions of the form xj = Re(Ajeiωt) can
be found. For solutions of this form the equations of motion reduce to
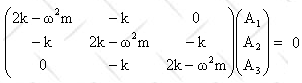 .
.
We can find the ω2 from det(kij -
ω2Tij) = 0. For a system with n degrees of
freedom, n characteristic frequencies ωa can be found. Our
system has 3 degrees of freedom.
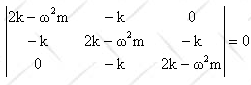 .
.
(2k - ω2m)3 - 2k2(2k -
ω2m) = 0.
(i) (2k - ω2m) = 0, ω12
= 2k/m, A2 = 0, A1 = -A3.
(ii) (2k - ω2m)2
- 2k2 = 0. ω22 = (2 + √2)k/m, A3
= A1, A2 = - √2A1.
(iii) ω32
= (2 - √2)k/m, A3 = A1, A2 =
√2A1.
Problem:
Two particles of mass m and one particle of mass M are constrained to move on
a line as shown. They are connected by massless springs with spring constant k.
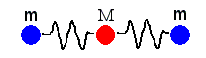
Find the normal modes and eigenfrequencies of the system, keeping M/m finite.
Solution:
- Concepts:
Coupled oscillations, normal modes
- Reasoning:
We are asked to find the normal modes of coupled harmonic oscillators.
- Details of the calculations:
The kinetic energy is T = ½[ m(dx1/dt)2 + M(dx2/dt)2
+ m(dx3/dt)2],
and the potential energy is U = (k/2)[(x2 - x1)2
+ (x3 - x2)2].
U = (k/2)[x12 + 2x22 + x32
- x1x2 - x2x1 - x2x3
- x3x2].
The xi are the displacements from the equilibrium positions. We
use the xi as our generalized coordinates qi.
The Lagrangian is L = T - U. This can be put into the form
L = ½∑ij[Tij(dqi/dt)(dqj/dt) - kijqiqj]
with Tij = Tji, kij = kji.
Here T11 = T33 = m, T22 = M, Tij(i≠j)
= 0,
k11 = k33 = k, k22 = 2k, k12 = k21
= k23 = k32 = -k, k13 = k31 = 0.
Solutions of the form xj = Re(Ajeiω t) can
be found. For solutions of this form the equations of motion reduce to:
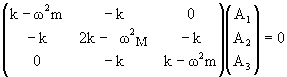

(k - ω2m)2(2k - ω2M) - 2k2(k - ω
2m) = 0.
Solution 1: k - ω2m = 0, ω = (k/m)½.
If k - ω2m ≠ 0, then (k - ω2m)(2k - ω2M) =
2k2. ω2(ω2mM - kM - 2km) = 0.
Solution 2: ω = 0.
Solution 3: ω = (k/m + 2k/M)½.
The displacements for each mode are determined from the equations of motion.
Solution 1: ω = (k/m)½.
Equation 1 yields kA2 = 0, equation 2 then yields kA1
+ kA3 = 0.
A1 = - A3, A2 = 0, the central mass is
stationary, m1 and m3 move in opposite directions with
equal amplitudes.
Solution 2: ω = 0.
A1 = A2 = A3, translation of the CM, no
relative motion.
Solution 3: ω = (k/m + 2k/M)½.
The displacements
Equation 1 yields -(2m/M)A1 = A2.
Equation 3 yields -(2m/M)A3 = A2.
A1 = A3 = -(M/(2m))A2, the central mass
move in a direction opposite to the direction of the outer masses.
Problem:
Two masses a and b are on a horizontal surface. Mass b has a spring
connected to it and is at rest. Mass a has an initial velocity v0
along the x-axis and strikes the spring of constant k, compressing it and thus
starting mass b in motion along the x-axis.
(a) Find the maximum force exerted.
(b) Find the resulting motion of mass a
while in contact with the spring.
Solution:
- Concepts:
Small oscillations, coupled oscillations, normal modes
L = ½∑ij[Tij(dqi/dt)(dqj/dt) - kijqiqj]
with Tij = Tji, kij = kji.
Solutions of the form qj = Re(Ajeiωt) can
be found. We can find the ω2 from det(kij - ω2Tij)
= 0.
- Reasoning:
During the time interval that both masses are in contact with the spring,
they can be treated as coupled harmonic oscillators.
- Details of the calculations:
(a) Assume that at t = 0 mass a makes contact with the spring. At t = 0
both masses are at their equilibrium position. Let xa(t) and xb(t)
denote the their displacements from their equilibrium positions,
respectively.
In the collision energy and momentum are conserved.
Ti = Tf + U, Pi = Pf. The
maximum force is exerted when the spring has maximum compression. At that
instant both masses move with the same velocity.
½mav02 = ½(ma + mb)v2
+ ½k(xb - xa)min2.
mav0 = (ma + mb)v.
Combining the two equations we have (xb - xa)min
= (mamb/k)½ v0/(ma
+ mb)½.
The maximum force is k(xb - xa)min = (kmamb)½
v0/(ma + mb)½.
(b) T = ½ma(dxa/dt)2 + ½mb(dxb/dt)2,
U = ½k(xb - xa)2 = ½k(xb2
+ xa2 - xaxb - xbxa).
T11 = ma, T22 = mb, k11
= k22 = k, k12 = k21 = -k.
det(kij
- ω2Tij) = 0 --> ω1 =
0, ω22 = k(ma + mb)/(mamb).
For ω1 = 0 we have A1 = A2. For ω22
= k(ma + mb)/(mamb) we have A2
= -(ma/mb)A1.
The most general solutions are:
xa = A1t + B1cos(ωt +
φ), xb =
A1t - (ma/mb)B1cos(ωt + φ),
dxa/dt = A1 - ωB1sin(ωt + φ), dxb/dt
= A1 + ω(ma/ma)B1sin(ωt +
φ).
The initial conditions at t = 0 are xa = xb = 0, dxa/dt
= v0, dxb/dt = 0.
This implies B1cos(φ) = 0,
φ =
π/2.
v0 = A1 - ωB1, A1 + ω(ma/mb)B1
= 0.
A1 = v0ma/(ma + mb),
B1 = -(1/ω)v0mb/(ma + mb).
Therefore
xa = (v0/ω)mb/(ma + mb)sinωt
+ mav0/(ma + mb)t,
dxa/dt = v0mb/(ma + mb)cosωt
+ mav0/(ma + mb),
as long as mass a is in contact with the spring.
[At t = 0 we have dxa(lab) /dt = v0mb/(ma
+ mb) + mav0/(ma + mb)
= v0.]
A different approach:
Solution:
- Concepts:
Simple harmonic motion, frame transformations, two interacting particles
- Reasoning:
In the center of mass frame we have an elastic collision between two
particles with an interaction energy U(x) = ½k(x-x0)2,
where x-x0 is the distance between the particles, as long as
particle a is in contact with the spring .
- Details of the calculations:
(a) In the center of mass frame we have an elastic collision. Assume mass
a approaches the CM with with speed va from the left, and mass b
approaches the CM with speed vb from the right. The CM is
at rest and mass a recedes from the CM with with speed va to the
right, while mass b recedes from the CM with with speed vb to the
left after the collision.
We have mava = mbvb in the CM
frame before the collision. To find the relationship between the speeds in
the CM and the lab frame we use
ma(v0 - vb) = mbvb.
vb = mav0/(ma + mb)),
va = mbv0/(ma + mb).
The maximum force is exerted when all the kinetic energy is converted into
potential energy.
Fmax = k(xmin-x0).
k(xmin-x0)2 = mava2
+ mbvb2 = ma(mbv0/(ma
+ mb))2 + mb(mav0/(ma
+ mb))2 = mambv02/(ma
+ mb).
k(xmin-x0) = (kmamb)½
v0/(ma + mb)½.
(b) Assume that mass a makes contact with the spring at t = 0, at the
origin of the CM and the lab frame. (We assume that at t = 0 the origin of
the two frames coincide.) Assume that at t = 0 the distance between mass a
and mass b is x0.
In the CM frame when mass a moves a distance xa to the right,
mass b moves a distance xb = xa(ma/mb)
to the left. The distance between the masses becomes x = x0 - (xa
+ xb) = x0 - xa(ma + mb)/mb
= x0 - x'.
For t > 0 we have U = ½kx'2 = ½[k(ma + mb)2/mb2]xa2
until the time when contact is lost again.
The kinetic energy of the particles is
T = ½ma(dxa/dt)2 + ½mb(dxb/dt)2
= ½(ma + ma2/mb)(dxa/dt)2.
L = T - U = ½(ma(mb + ma)/mb)(dxa/dt)2
- ½)[k(ma + mb)2/mb2]xa2.
This is a Lagrangian for simple harmonic motion.
d2xa/dt2 = -k(mb + ma)/(mamb)xa
= -(k/μ)xa, with μ = mamb/(mb +
ma).
We therefore have
xa = Asinωt, ω = (k/m)½, until t = π/ω (½ period
of the motion).
dxa/dt = ωAcosωt.
At t = 0 we have ωA = va = mbv0/(ma
+ mb), A = mbv0/[ω(ma + mb)]
In the lab frame we have xa(lab) = xa + vbt.
The motion of mass a is described by
xa(lab) = (v0/ω)mb/(ma + mb)sinωt
+ mav0/(ma + mb)t,
dxa(lab) /dt = v0mb/(ma + mb)cosωt
+ mav0/(ma + mb),
as long as mass a is in contact with the spring.
[At t = 0 we have dxa(lab) /dt = v0mb/(ma
+ mb) + mav0/(ma + mb)
= v0.]
Problem:
Use Lagrange's equations to find the normal modes and normal frequencies for
linear vibrations of the CO2 molecule shown below.
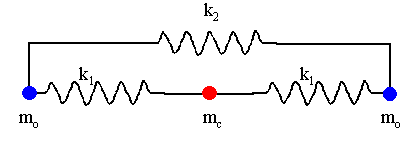
Solution:
- Concepts:
Small oscillations, normal modes
L = ½∑ij[Tij(dqi/dt)(dqj/dt) - kijqiqj]
with Tij = Tji, kij = kji.
Solutions of the form qj = Re(Ajeiωt) can
be found. We can find the ω2 from det(kij - ω2Tij)
= 0.
- Reasoning:
We are asked to find the normal modes of the system.
- Details of the calculations:
We are only
considering linear vibrations.
Let qi denote the displacement
of the ith particle from its equilibrium position.
qi = xi
- xi0.
Then
T = ½[mo(dq1/dt)2
+ mc(dq2/dt)2 + mo(dq3/dt)2].
U = ½k1[(q2 - q1)2 + (q3
- q2)2] + ½k2[(q3 - q1)2].
U = ½(k1 + k2)q12 + ½(k1
+ k2)q32 + k1q22
- ½k1(q2q1 + q1q2
+ q3q2 + q2q3)
- ½k2(q3q1
+ q1q3).
T11 = T33 = mo,
T22 = mc, Tij(i ≠ j) = 0.
k11
= k33 = k1 + k2, k22 = 2k1,
k12 = k21 = k32 = k23 = -k1,
k31 = k13 = -k2.
det(kij
- ω2Tij) = 0.
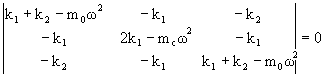 .
.
ω2 = 0, or
ω2 = (k1/mc + k1/mo +
k2/mo) ± (k1/mc - k2/mo).
To find the relative displacements we solve the system of equations
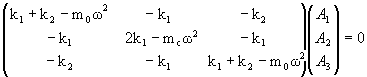
for each ω.
| ω2 = 0: |
uniform linear motion, A1 = A2 = A3. |
|
| ω2 = 2k1/mc + k1/mo:
|
A3 = A1, A2 = -(2mo/mc)A1. |
<--o o----> <--o |
| ω2 = k1/mo + 2k2/mo: |
A3 = -A1, A2 = 0. |
o---> o <---o |
Problem:
A particle of mass m is attached to a rigid support by a spring with a force
constant k. At equilibrium, the spring hangs vertically downward. To
this mass-spring combination is attached an identical oscillator, the spring of
the latter being connected to the mass of the former.
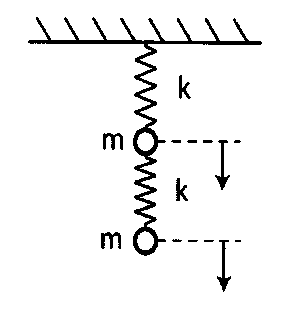
(a) Show that by appropriate choice of coordinates and their zero-points the
equations of motion can be expressed as
md2x1/dt2
+ 2kx1 - kx2 = 0,
md2x2/dt2
+ kx2 - kx1 = 0.
(b) Calculate the characteristic
frequencies for one-dimensional vertical oscillations.
(c)
Qualitatively describe the normal modes of the system with a short discussion
plus drawings.
(d) Quantitatively compare the characteristic
frequencies with the frequencies when either of the particles is held fixed
while the other oscillates.
Solution:
- Concepts:
Lagrangian
mechanics, coupled oscillations
- Reasoning:
We are asked to find the normal modes of coupled harmonic
oscillators.
- Details of the calculation:
(a) T = ½m(dy1/dt)2
+ ½m(dy2/dt)2, U = ½ky12 + ½k(y2
- y1)2 - mgy1 - mgy2.
Here y1
and y2 are the displacements of the springs from their respective
equilibrium positions. The y-axis points down.
Let y1 = x1
+ a, y2 = x2 + b.
T = ½m(dx1/dt)2
+ ½m(dx2/dt)2,
U = kx12 +
ka2 + 2kx1a + ½kx22 + ½kb2
+ kx2b - kx1x2 - kab - kx1b - kx2a
- mgx1 - mgx2 - mga - mgb - constant.
The zero of
the potential energy can be chosen arbitrarily.
To put the potential
energy function into the form U = ½∑ijkijxixj,
let ka2 + ½kb2- kab - mga - mgb = constant.
Choose
2ka - kb - mg = 0, kb - ka - mg = 0, which implies that ka = 2mg, kb = 3mg.
Then x1 and x2 are the displacements from the
equilibrium positions in the gravitational potential near the surface of
Earth,
and T = ½m(dx1/dt)2 + ½m(dx2/dt)2,
U = kx12 + ½kx22 - kx1x2,
L = T - U.
Lagrange's equations become
md2x1/dt2
+ 2kx1 - kx2 = 0,
md2x2/dt2
+ kx2 - kx1 = 0.(b) Assume x1 =
Re(A1 exp(iωt)), x2 = Re(A2 exp(iωt)).
Then
 .
.
ω2 = [3/2 ± √5/2](k/m), ω12 = [3/2 +
√5/2](k/m), ω22 = [3/2 - √5/2](k/m).
ω1 = 1.62 (k/m)½, ω2 = 0.62
(k/m)½.
(c) ω = ω1: A2 = -½A1(√5 - 1) =
-0.62 A1.
ω = ω2: A2 = ½A1(√5 + 1) = 1.62 A1.

(d) When particle 1
is held fixed (x1 = 0), then particle 2 oscillates with angular
frequency ω, where ω = (k/m)½.
When particle 2 is held fixed
(x2 = 0), then particle 1 oscillates with angular frequency ω,
where ω = (2k/m)½ = 1.41 (k/m)½.
The separation
of the characteristic frequencies of the coupled system is greater than the
separation of the single particle frequencies.
Problem:
Four mass points of mass m move on a circle of radius R. Each mass point is
coupled to its two neighboring points by a spring constant k.
(a) Find the Lagrangian of the system, and derive the equations of motion of
the system.
(b) Calculate the eigen-frequencies of the system, and discuss the related
eigen-vibrations.
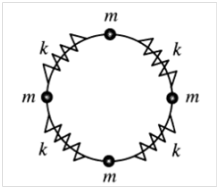
Solution:
- Concepts:
Coupled oscillations
- Reasoning:
L = ½∑ij[Tij(dqi/dt)(dqj/dt)
- kijqiqj] with Tij = Tji,
kij = kji.
Here Tii
= m, Tij(i ≠ j) = 0, i, j = 1, 2, 3, 4, (cyclic).
kii = 2k, kij = -k if j = i ± 1, kij = 0
otherwise.
Equations of motion:
d/dt(∂L/∂(dqi/dt)) -
∂L/∂qi = 0.
Solutions of the form qj = Re(Ajeiω t) can
be found. For a system with n degrees of freedom, n characteristic
frequencies ωα can be found. Some frequencies may be
degenerate. For a particular frequency ωα we solve
∑j[kij - ωα2Tij]Ajα
= 0
to find the Ajα. Since it is difficult to evaluate the
determinant of a 4 x 4 matrix, we find the solutions of this system of
coupled equations using physical insight.
(a)
d/dt(∂L/∂(dqi/dt)) -
∂L/∂qi = 0.
(-kqi-1 + 2kqi - kqi+1) + md2qi/dt2
= 0, i,j = 1, 2, 3, 4, (cyclic).
- Details of the calculation:
(b) 1.) ω1 = 0, A1 = A2 = A3 =
A4, ∑jkij = 2k - 2*k = 0.
All other modes can have no net angular momentum.
2.) Assume A1 and A3 are fixed. A1 = A3
= 0, A2 = -A4.
The equation of motion for i = 2 is k21A1 + k22A2
+ k23A3 - ω22T22 A2
= 0,
2k - ω22m = 0, ω22 = 2k/m.
3.) Assume A2 and A4 are fixed. A1 = -A3
= 0.
For this mode ω32 = 2k/m. Mode 2 and 3
are degenerate. Any linear combination of these modes is also a normal
mode. For example, the mode with A1 = A4 , A2
= A3 = -A1 is a linear combination
of modes 2 and 3 and is not linearly independent.
4.) Assume A1 = A3, A2 = A4, A1
= - A2.
The equation of motion for i = 2 is k + 2k + k - ω22m
= 0, ω42 = 4k/m.For the eigen-vibrations we have:
1.) qi = vt. (uniform rotation)
2.) q1 = q3 = 0, q2 = C2cos(ω2t
+ φ2), q4 = -C2cos(ω2t + φ2)
3.) q2 = q4 = 0, q3 = C3cos(ω3t
+ φ3), q1 = -C3cos(ω3t + φ3)
4.) q1 = q3 = C4cos(ω4t + φ4),
q2 = q4 = -C4cos(ω4t + φ4)
The Ci and φi depend on the initial conditions. The
mode with the highest frequency is mode 4 (non-degenerate) and the mode with
the lowest frequency is mode 1 (non-degenerate).
Problem:
Consider six equal masses constrained to move on a circle of fixed radius and
connected by identical springs of spring constant k.
(a) Find the normal mode frequencies of the system for small displacement of
the masses.
(b) Find the (time dependent) displacement of the masses for each normal mode.
Give a physical description of the motion of the masses for normal modes with
the highest and lowest frequencies.
Solution:
- Concepts:
Coupled oscillations
- Reasoning:

L = ½∑ij[Tij(dqi/dt)(dqj/dt)
- kijqiqj] with Tij =
Tji, kij = kji.
Here Tii
= m, Tij(i ≠ j) = 0, i, j = 1, 2, 3, 4, 5, 6, (cyclic).
kii = 2k, kij = -k if j = i ± 1, kij = 0
otherwise.
Solutions of the form qj = Re(Ajeiω t) can
be found. For a system with n degrees of freedom, n characteristic
frequencies ωα can be found. Some frequencies may be
degenerate. For a particular frequency ωα we solve
∑j[kij - ωα2Tij]Ajα
= 0
to find the Ajα. Since it is difficult to evaluate the
determinant of a 6 x 6 matrix, we find the solutions of this system of
coupled equations using physical insight.
- Details of the calculation:
(a)
1.) ω1 = 0, A1 = A2 = A3 = A4
= A5 = A6, ∑jkij = 2k -
2k = 0.
All other modes must have zero total or net angular momentum
2.) Assume A1 and A4 are fixed. A1 = A4
= 0, A2 = A3, A5 = A6, A2
= - A5.
The equation of motion for i = 2 is k21A1 + k22A2
+ k23A3 - ω22T22 A2
= 0,
2k - k - ω22m = 0, ω22 = k/m.
3.) Assume A2 and A5 are fixed. A2 = A5
= 0, A3 = A4, A1 = A6, A3
= - A6.
For this mode ω32 = k/m. Mode 2 and 3 are
degenerate. Any linear combination of these modes is also a normal mode.
The mode with A3 = A6 = 0, A1 = A2,
A4 = A5, A1 = - A4 is a linear
combination of modes 2 and 3 and is not linearly independent.
4.) Assume A1 and A4 are fixed. A1 = A4
= 0, A2 = A5, A3 = A6, A2
= - A3.
The equation of motion for i = 2 is 2k + k - ω22m =
0, ω42 = 3k/m.
5.) Assume A2 and A5 are fixed. A2 = A5
= 0, A3 = A6, A1 = A4, A3
= - A4.
For this mode ω52 = 3k/m. Mode 4 and 5 are
degenerate. Any linear combination of these modes is also a normal mode.
6.) Assume A1 = A3 = A5, A2 = A4
= A6, A1 = - A2.
The equation of motion for i = 2 is k + 2k + k - ω22m
= 0, ω62 = 4k/m.
(b)
1.) qi = vt.
2.) q1 = q4 = 0, q2 = q3 = C2cos(ω2t
+ φ2), q5 = q6 = -C2cos(ω2t
+ φ2)
3.) q2 = q5 = 0, q3 = q4 = C3cos(ω3t
+ φ3), q6 = q1 = -C3cos(ω3t
+ φ3)
4.) q1 = q4 = 0, q2 = q5 = C4cos(ω4t
+ φ4), q3 = q6 = -C4cos(ω4t
+ φ4)
5.) q2 = q5 = 0, q3 = q6 = C5cos(ω5t
+ φ5), q1 = q4 = -C5cos(ω5t
+ φ5)
6.) q1 = q3 = q5 = C6cos(ω6t
+ φ6), q2 = q4 = q6 = -C6cos(ω6t
+ φ6)
The Ci and φi depend on the initial conditions. The
mode with the highest frequency is mode 6 (non-degenerate) and the mode with
the lowest frequency is mode 1 (non-degenerate).
Problem:
Three point masses of mass m move on a circle of radius
R. The equilibrium positions are shown in the figure. Each point
mass is coupled to its two neighboring points
by a spring with spring constant k.
(a) Write down the Lagrangian of the system.
(b) Find the normal modes of the system.
(c) If at t = 0 mass 1 is displaced from its equilibrium position
clockwise by 9o, what is the subsequent motion of all the
masses?

Solution:
- Concepts:
Coupled
oscillations
- Reasoning:
If L = ½∑ij(Tij(dqi/dt)(dqj/dt) - kijqiqj),
the solutions of the form qj = Re(Ajeiωt) can
be found. We can find the ω2 from det(kij - ω2Tij)
= 0. For a system with n degrees of freedom, n characteristic frequencies ωα
can be found. While the secular equation det(kij - ω2Tij) = 0 can in principle always be
solved, it is often simpler to find the normal modes by using physical insight
and noting the symmetries of the system.
- Details of the calculation:
(a) T =
½m((dq1/dt)2 + (dq2/dt)2 + (dq3/dt)2),
U = ½k((q2 - q1)2 + (q3 - q2)2
+ (q1 - q3)2),
L = T - U = ½∑ij(Tij(dqi/dt)(dqj/dt)
- kijqiqj).
The qi are the displacements of the masses from their equilibrium
positions, qi = rθi.
Here Tii = m, Tij(i≠j) = 0, kii = 2k, kij(i≠j)
= -k for i, j = 1, 2, 3.
(b) Equations of motion:
Solutions of the form qj = Re(Ajeiωt) can
be found.
We can find the ω2 from det(kij - ω2Tij)
= 0. For a system with n degrees of freedom, n characteristic frequencies ωα
can be found. Some frequencies may be degenerate.
For a particular frequency ωα we solve ∑j(kij
- ω2Tij) Ajα = 0 to find the Ajα.
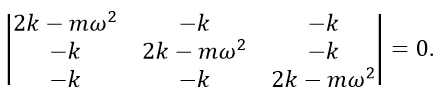
ω2(ω4 - 6(k/m) ω2 + 9(k/m)2 =
0, ω12 = 0, ω22 = ω32
= ω2 = 3k/m.
ω12 = 0: A1 = A2 = A3,
constant displacement or uniform circular motion.
For the degenerate frequency we pick two linearly independent modes.
ω22 = 3k/m. A2 = 0, A1 = -A3.
ω32 = 3k/m. A3 = 0, A1 = -A2.
(c) The most general solution for each coordinate qj is a sum of
simple harmonic oscillations in all of the frequencies ωα.
q1(t) = Re(A + (B + C)exp(iω t)), q2(t) = Re(A -
Cexp(iω t)), q3(t) = Re(A - Bexp(iω t)),
dq1(t)/dt = Re(iω(B+C)exp(iω t)), dq2(t)/dt = Re(-iωCexp(iω
t)), dq3(t)/dt = Re(-iωBexp(iω
t)).
Given: q1(0) = Re(A + B + C) = D, D = R*9o=
9*0.05π,
q2(0)
= Re(A - C) = 0, q3(0) = Re(A - B) = 0.
Therefore Re(A) = Re(B) = Re(C) = D/3.
dq1/dt = dq2/dt = dq3/dt = 0 at t = 0.
Therefore Im(A) = Im(B) = Im(C) = 0.
q1(t)/ = (D/3)(1 + 2cos(ωt)), θ1(t) = 3o(1
+ 2cos((3k/m)½t)),
θ2(t) = θ3(t) = 3o(1 - cos((3k/m)½t)).
Problem:
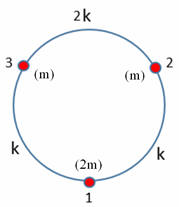
Three point masses, one of mass 2m and two of mass m are constrained to move
on a circle of radius R. Each mass point is coupled to its two neighboring
points by a spring. The springs coupling mass 1 and 3 and mass 1 and 2
have spring constant k, and the spring coupling mass 2 and mass 3 has spring
constant 2k. Find the normal modes of the system.
Solution:
- Concepts:
Coupled oscillations
- Reasoning:
If L = ½∑ij(Tij(dqi/dt)(dqj/dt)
- kijqiqj), the solutions of the form qj
= Re(Ajeiωt) can be found. We can find the ω2
from det(kij - ω2Tij) = 0. For a system
with n degrees of freedom, n characteristic frequencies ωα can be
found. While the secular equation det(kij - ω2Tij)
= 0 can in principle always be solved, it is often simpler to find the
normal modes by using physical insight and noting the symmetries of the
system.
- Details of the calculation:
Formal approach:
T = m(dq1/dt)2
+ ½m(dq2/dt)2 + ½m(dq3/dt)2,
U = ½k(q2 - q1)2 + k(q3 - q2)2
+ ½k(q1 - q3)2).
L = T - U = ½∑ij(Tij(dqi/dt)(dqj/dt)
- kijqiqj).
The qi are the
displacements of the masses from their equilibrium positions, qi
= rθi.
Here T11= 2m, T22 = T33
= m, Tij(i≠j) = 0,
k11 = 2k, k22 = k33
= 3k, k12 = k21 = k13 = k31 =
-k, k23 = k32 = -2k.
ω2(ω4 -
7(k/m)ω2 + 10(k/m)2) = 0, ω12 =
0, ω22 = 2k/m, ω32 = 5k/m.
ω12
= 0 --> A1 = A2 = A3, constant
displacement or uniform circular motion.
ω22 =
2k/m --> A2 = A3 = -A1. ω32
= 5k/m --> A1 = 0, A2 = -A3.
Using physical insight:
Equations of motion:
(2k - 2mω2)A1
- kA2 - kA3 = 0, (3k - mω2)A2 -
2kA3 - kA1 = 0,
(3k - mω2)A3
- kA1 - 2kA2 = 0.
(i) An angular displacement of
the system as a whole does not stretch any spring, A1 = A2
= A3. Then ω2 = 0.
(ii) Mass 1 can stay fixed (A1
= 0) if A3 = -A2. Then (3k - mω2)A2
+2kA2 = 0, ω2 = 5k/m.
(iii) The system cannot have
an angular displacement as a whole. Assume A2 = A3 =
-A1.
Then (2k - 2mω2)A1 + kA1
+ kA1 = 0, ω2 = 2k/m.
Problem:
A large number N (N = even) of point masses m are connected by identical
springs of equilibrium length a and spring constant k. Let qi
(i = 0 to N - 1) denote the displacement of the ith mass from its equilibrium
position. Assume periodic boundary conditions, qi = qi+N.
(You can, for example imagine the masses arranged on a large circle of
circumference Na.)
(a) Write down the Lagrangian for the system of N
point masses.
(b) Find the equation of motion for the jth point mass.
(c) Assume solutions of the form qj(t) = |A|exp(iφj)
exp(-iωt) = |A|exp(i(φj - ωt)) exist, where ω is a normal mode
frequency.
Assume the phase of the amplitude depends on the position
of the mass and write φj = p*ja.
What are the restrictions on p
due to the boundary conditions?
(d) Find the N normal mode frequencies
ωn. Make a sketch of ωn as a function of mode number
n.
Solution:
- Concepts:
Lagrangian Mechanics, coupled oscillations, normal modes
- Reasoning:
This is a one-dimensional problem. We are asked to find
the normal modes of coupled harmonic oscillators.
- Details of the calculation:
(a) L = T - U = ∑i = 0N-1[½m(dqi/dt)2
- ½k(qi+1 - qi)2]
= ∑i = 0N-1[½m(dqi/dt)2
- ½k(qi+12 + qi2 - 2qiqi+1].
(b) d/dt(∂L/∂(dqj/dt)) - ∂L/∂qj = 0.
The terms in
the Lagrangian that depend on qj an dqj/dt are
½m(dqj/dt)2 - ½k(2qj2 - 2qj-1qj
- 2qjqj+1).
(They come from the terms in the sum i
= j and i + 1 = j.)
The equation of motion for the jth point mass
therefore is
md2qj/dt2 - k(qj+1
- 2qj + qj-1) = 0.
(c) Assume qj(t) =
|A|exp(i(p*ja - ωt). The periodic boundary conditions imply that
p*ja =
p*(j + N)a ± n*2π, pnNa = n*2π, pn = n2π/(Na), n =
integer.
(d) Inserting solutions of the form qj = |A|exp(i(pn*ja
- ωt)) into the equation of motion we obtain
-mωn2
exp(ipn*ja) - k[exp(ipn*(j+1)a) - 2exp(ipn*ja)
+ exp(ipn*(j-1)a)] = 0,
or
ωn2 =
-(k/m)[exp(ipn*a) - 2 + exp(-ipn*a)] = -¼ω02[2cos(pn*a)
- 2]
= ½ω02[1 - cos(pn*a)] = ω02sin2(pn*a/2)
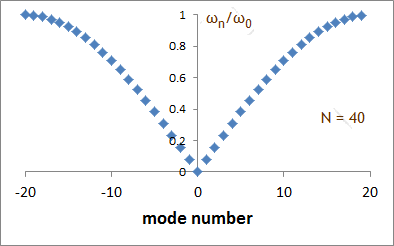
= ω02sin2(nπ/N).
Here ω02
= 4k/m.
ωn = ω0|sin(nπ/N)| are the normal mode
frequencies.
There are N frequencies which we can label with a mode
number from n = -N/2 to (N/2 -1). All but two of the frequencies are
two-fold degenerate.


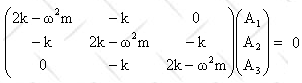 .
.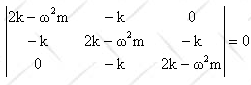 .
.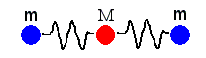
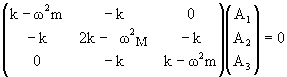


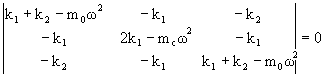 .
.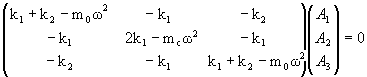

 .
.