Mechanical waves

Waves on strings, traveling waves

Problem:

A helicopter accelerates upward with a cable of mass 8 kg and length 17 m attached to a mass of 150 kg hanging vertically below it.  If a transverse pulse initiated by wobbling of the mass takes 0.238 seconds to travel the length of the cable, what is the upward acceleration of the helicopter?

Solution:

• Concepts:
  Waves on a string
• Reasoning:
  For waves on a string v = (T/μ)^½.  Knowing T we solve for a using T - mg = ma.  Since the mass of the cable is small compared to the hanging mass, make the approximation that the tension is uniform.
• Details of the calculation:
  Here μ = (8 kg)/(17 m) and v = (17 m)/(0.238 s).   The tension in the cable therefore is T = μv² = 2499 N.
  For the 150 kg mass we have
  T - mg = ma,  a = T/m - g = 2400 N/150 kg - 9.8 m/s²  = 6.2 m/s².

Problem:

A rope of uniform linear density μ and total length L is suspended from one end.  It hangs vertically under its own weight.  It is lightly tapped at the lower end.  How long does it take for the perturbation to reach the top of the rope?

Solution:

• Concepts:
  Waves on a string
• Reasoning:
  For waves on a string v = (T/μ)^½.
• Details of the calculations:
  The tension at at height z above the lower end is T = μgz.
  The local speed of the wave is v = (T(z)/μ)^½ = (gz)^½.
  The propagation time is t = ∫₀^Ldz/v(z) = ∫₀^Ldz/(gz)^½ = 2(L/g)^½.

Problem:

A wire of length L and mass M has a non-uniform mass per unit length m = kx, where x is the distance from one end of the wire.  The tension in the wire is F
(a)  Determine k in terms of M and L.
(b)  How long does it take for a transverse wave pulse to travel from one end to the other end of the wire.  Express your answer in terms of M, L, and F.

Solution:

• Concepts:
  Waves on a string
• Reasoning:
  For waves on a string v = (T/μ)^½.
• Details of the calculations:
  (a)  M = ∫₀^Lkxdx = kL²/2,  k = 2M/L².
  (b)  v = dx/dt = (F/μ)^½ = (F/kx)^½.
  dt = (k/F^)½√x dx,  T = (k/F^)½∫₀^L√x dx = (k/F^)½ (2/3) L^3/2 = (8ML/(9F))^½.
  It takes a wave pulse time T to travel from one end to the other end of the wire.

Waves on strings, standing waves

Problem:

A rope has a mass of 2 kg and a length of 10 m.  It is stretched with a tension of 50 N and fixed at both ends.  What is the frequency of the first harmonic on this rope?

Solution:

• Concepts:
  Standing waves on a string
• Reasoning:
  An integer number of half-wavelengths have to fit into the length L of the string.
• Details of the calculation:
  nl/2 = L, l = 2L/n.
  f_n = nv/(2L) = nf₁.
  v = (F/μ )^½,  F = tension in the string, μ  = mass per unit length.
  μ  = m/L = 0.2 kg/m, v² = F/μ  = 50 N/(0.2 kg/m) = 250 (m/s)²,  v = 15.8 m/s.
  The wavelength of the first harmonic is 20 m.  The frequency f is f = v/(20 m) = (15.8/20) Hz = 0.79 Hz.

Problem:

A transverse wave propagates in an infinitely long wire of mass per unit length 100 g/m and with a tension of 10 N.  An observer next to the wire notices 10 crests passing him in a time of 2 seconds moving to the left.
(a)  What is the wave velocity on the wire?
(b)  What is the frequency of the wave?
(c)  What is the wavelength?
(d)  If at t = 0 and x = 0 the displacement assumes its maximum value of 1 mm, what is the equation of the wave?
(e)  The wire is now fixed, under the same tension, at two points separated by 0.15 meters.  What is the frequency of the third harmonic?

Solution:

• Concepts:
  Waves on a string
• Reasoning:
  For waves on a string v = (T/μ)^½.
• Details of the calculation:
  (a)  v = (T/μ)^½ = (10 N/(0.1 kg/m))^½ = 10 m/s.
  (b)  f = 10/(2 s) = 5 Hz.
  (c)  λ = v/f = 2 m.
  (d)  y(x,t) = (1 mm)cos(πx + 10πt).
  (e)  λ = 0.1 m,  f = v/λ = 100 Hz.

Problem:

A string that has a linear mass density of 4*10^-3 kg/m is under tension of 360 N and fixed at both ends.  One of the resonance frequencies is 375 Hz.  The next higher resonance frequency is 450 Hz.
(a)  What is the fundamental frequency of the string?
(b)  Which harmonics have the given frequencies?
What is the length of the string?

Solution:

• Concepts:
  Standing waves on a string
• Reasoning:
  For a string v = √(T/μ).  Here v = (360/4*10^-3)^½ m/s = 3*10² m/s.  For a string fixed at both ends to support a standing wave, the length of the string must equal an integer number of half-wavelength of the standing wave.
• Details of the calculation:
  L = nλ_n/2.  λ_nf_n = v.
  f_n = nv/(2L) is the frequency of the nth harmonic.
  f_n/f_n+1 = 375/450 = n/n+1, n = 5.
  (a)  Fundamental frequency f₁ = f₅/5 = 75 Hz
  (b)  The given frequencies are the fifth and sixth harmonic.
  (c)  L = v/(2f₁) = 2 m.

Sound waves

Problem:

You are given a microphone hooked up to a frequency analyzer and asked to measure the sound velocity in a steel bar of length L = 0.5 m by measuring the frequency of sound waves generated when the bar is struck by a steel mallet. 
(a)  Assuming that the bar is supported by a rigid clamp at the center of the bar, derive the relationship between the measured frequencies and the wave velocity.  Be sure to carefully state the boundary conditions used to derive the standing wave patterns from the reflected traveling waves.
(b)  What is the sound velocity if the fundamental frequency is 3500 s^-1?
(c)  When the end of the bar is struck parallel and perpendicular to the bar's axis, different fundamental frequencies are measured.  Explain why and indicate which you expect to have the higher fundamental frequency.

Solution:

• Concepts:
  Standing waves
• Reasoning:
  Striking the bar sets up a standing wave with a node at the center and antinodes at the end.
• Details of the calculation:
  (a)  L = (n + ½)λ, n = 0, 1, 2, ... .
  λf = v, Lf/(n + ½) = v.
  (b) fundamental:  2Lf = v.  v = 3500 m/s.
  (c)  We can set up transverse or longitudinal waves.  I expect the longitudinal (compression) waves to have the higher fundamental frequency, because they have the higher speed.

Problem:

A vibrating tuning fork is held above a column of air as shown in the diagram.  The reservoir is raised and lowered to change the water level, and therefore the length of the column of air.  The shortest length of air column that produces a resonance is L₁ = 0.25 m, and the next resonance is heard when the length of the air column is L₂ = 0.8 m.  The speed of sound in air (at 20 ^oC, the temperature during the experiment) is 343 m/s and the speed of sound in water is 1490 m/s.

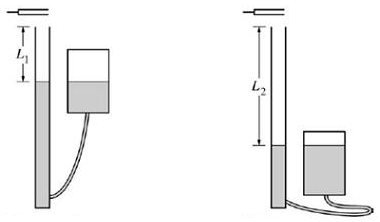
(a)  Calculate the wavelength of the standing sound wave produced by the tuning fork.
(b)  Calculate the frequency of the tuning fork that produces the standing wave.
(c)  Calculate the wavelength of the sound wave produced by this tuning fork in water.

Solution:

• Concepts:
  Standing waves
• Reasoning:
  For the longest wavelength standing wave in a tube of length L with one open end and one closed end (neglecting edge effects) we have L = λ/4.  For the next longest standing wave we have L = 3λ/4.
  [An odd-integer number of quarter wavelengths have to fit into the tube of length L.
  L = nλ/4,  λ = 4L/n,  f = v/λ  = nv/(4L),  n = odd.]
  
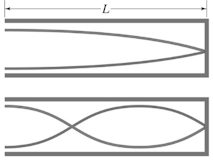
• Details of the calculation:
  (a)  In an experiment with a tube we always have edge effects.  We therefore look at the difference in tube length between the third harmonic and the fundamental for the same frequency.
  L₂ - L₁ = 0.8 m - 0.25 m = 0.55 m = λ/2,  λ = 1.1 m.
  (b)  f = v_s(air)/λ_air = (343 m/s)/(1.1 m) = 312 Hz.
  (c)  λ_water = v_s(water)/f = (1490 m/s)/(312 Hz) = 4.8 m.

Doppler shift

Problem:

(a)  Derive an expression for the frequency as a function of time that you would hear if you dropped a source of frequency f₀ from a tall tower.
(b)  Derive an expression for the frequency heard by an observer on the ground.

Solution:

• Concepts:
  The Doppler effect
• Reasoning:
  We have a moving source producing a sound wave.  The source is moving away from the observer on the tower and towards the observer on the ground.  The source is a freely falling object.  Its speed increases linearly with time, v = gt. 
• Details of the calculations:
  Assume a source is moving towards an observer with speed v_s.  It emits a beep every T seconds.  The sound travels with speed v towards the observer.  Assume beep i is emitted at t = 0, travels a distance d to the observer, and arrives at the observer at time d/v.  Beep (i + 1) is emitted at time T a distance d - <v_s>T from the observer and arrives at the observer at time (d - <v_s>T)/v + T.  The difference in the arrival times of the two beeps is 
  T' = (d/v) - (<v_s>T)/v + T - d/v =  (1 - <v_s>/v)T.
  Let f = observed frequency = 1/T', f₀ = frequency of source = 1/T.
  f = f₀v/(v - <v_s>).
  |<v_s>| = gt, where t is the time interval from the instant the source is dropped to the instant beep i is emitted plus T/2.
  (a)    <v_s> is negative  f = f₀*340/(340 + 9.8 t), where t is measured in seconds.
  (b)   <v_s> is positive  f = f₀*340/(340 - 9.8 t), where t is measured in seconds.

Problem:

A long diesel freight train is traveling horizontally at a speed v_t on a straight track.  As it approaches a tunnel in a sheer vertical wall, the engineer gives a long steady blast of the horn, whose principal frequency is f₀.  Both the horn itself and the echo from the wall are heard.
(a)  Show that the beat frequency heard by the engineer is given
f_b1 = f₀*2v_t/(v - v_t).
(b)  Show that the beat frequency heard by a stationary person on the ground near the rear of the train is given by
f_b1 = f₀*2vv_t/(v² - v_t²).
Here v is the speed of sound with respect to the air.

Solution:

• Concepts:
  Doppler shift
• Reasoning:
  If both source and observer are in motion, then the apparent frequency of the sound wave reaching the observer is
  f = f₀(v - v_obs)/(v - v_s)
  where v_obs and v_s are the components of the observer's and the source's velocity in the direction of the velocity of the sound reaching the observer.
• Details of the calculation:
  (a)  Horn:  The engineer is moving with the source, v_obs = v_s, f_H = f₀.
  Echo:  The echo reflects from the wall. 
  The frequency reflected from the wall (stationary observer, moving source) is
  f_W = f₀v/(v - v_s) = f_W = f₀v/(v - v_t).
  For the reflected sound heard be the engineer we have a stationary source and a moving observer.
  f_E = f_W(v - v_obs)/v = f_W(v + v_t)/v = f₀(v + v_t)/(v - v_t).
  The beat frequency heard by the engineer is |f₀ - f_E| = f₀*2v_t/(v - v_t).
  (b)  Horn:  The person on the ground is stationary, the source is moving.
  f_H = f₀v/(v - v_s) = f₀v/(v + v_t).
  (c)  Echo:  Both the source of the reflected wave and the observer are stationary.
  f_E = f_W = f₀v/(v - v_t).
  The beat frequency heard by the person on the ground is
  f₀ - f_E| = f₀|v/(v + v_t) - v/(v - v_t)| = f₀*2vv_t/(v² - v_t²).

Problem:

Two police cars have identical sirens that produce a frequency of f = 570 Hz.  A stationary listener is standing between two cars.  One car is parked and the other is approaching the listener and both have their sirens on.  The listener notices 2.6 beats per second.  Find the speed of the approaching police car (the speed of sound is v = 344 m/s).

Solution:

• Concepts:
  The Doppler effect
• Reasoning:
  We have a moving source producing a sound wave.  The source is moving towards the observer, the observer records a higher frequency f' = f v/(v - v_s), where v_s is the speed of the source.
  The superposition of the sounds waves with frequencies f and f' produces beats with beat frequency f' - f.
• Details of the calculation:
  f' - f = f (v/(v - v_s) - 1) = fv_s/(v - v_s) = 2.6/s.
  v_s/(v - v_s) = 2.6/570,  v_s(1 + 2.6/570) = v(2.6/570),  v_s = 1.56 m/s.