The Kepler problem
Kepler's third law
Problem:
Use Kepler's third law to calculate the mass of the sun, assuming that the
orbit of the earth around the sun is circular, with radius r = 1.5*108
km.
Solution:
- Concepts:
Kepler's third law
- Reasoning:
mv2/r = GMm/r2. v2 = GM/r. (2πr/T)2
= GM/r.
T2 = (4π2/(GM))r3, Kepler's third law.
- Details of the calculation:
T = 365 days = 3.15*107 s.
M = (4π2/(GT2))r3, M = 2.01*1030
kg.
Problem:
Haley's Comet approaches the sun to within 0.570 A.U., and its orbital period
is 75.6 years. (A.U. is the abbreviation for astronomical units, where 1 A.U. =
1.5*1011m is the mean Earth-Sun distance.) How far from the sun will
Haley's comet travel before it starts its return journey?
Solution:
- Concepts:
Motion in a central potential, Kepler's third law
- Reasoning:
We are asked to find Rmax, given Rmin and the period T
for a comet orbiting the sun. Since the mass of the sun (m1) is
much greater than the mass of the comet, we may consider the sun to be
stationary.
- Details of the calculation:
T2 = (4π2/Gm1)R3.
For elliptical orbits, R denotes the semi-major axis, R = (Rmax +
Rmin)/2.
R3 = Gm1T2/4π2.
R3 = (6.67*10-11 Nm2/kg2)(1.991*1030
kg)(75.6*365*24*60*60 s)2/4π2 = 1.91*1037
m3.
R = 2.67*1012 m = (Rmax + Rmin)/2.
Rmax = 5.35*1012 m - 0.570*1.5*1011 m =
5.26*1012 m.
Rmax is the maximum distance of the comet from the sun.
Problem:
The time of revolution of planet Jupiter around the Sun is
TJ ~ 12 years. What is the distance between Jupiter and the Sun if
the Earth-Sun distance is 150*106 km? Assume that the orbits
are circular.
Solution:
- Concepts:
Kepler's third law
- Reasoning:
T2 proportional R3.
- Details of the calculation:
RJ3 = RE3*TJ2/TE2
= (150*106 km)3*144. RJ = 7.86*108
km.
Problem:
A satellite of mass 200 kg is placed in Earth orbit at a height of 200 km
above the surface. It has a circular orbit. What is the period of
the satellite?
Given: REarth = 6.4*106 m, MEarth = 5.98*1024 kg
Solution:
- Concepts:
Motion in a central potential, Kepler's third law
- Reasoning:
We are asked to find the period T for a satellite orbiting
the Earth in a circular orbit. Since the mass of the Earth (m1)
is much greater than the mass of the satellite, we may consider the earth to
be stationary.
- Details of the calculation:
T2 = (4π2/Gm1)R3.
R is the radius of the circular orbit.
R = 6.4*106 m + 2*105
m = 6.6*106 m
R3 = 2.9*1020 m3
G = gravitational
constant = 6.67*10-11 N-m2/kg2
m1 = mass of Earth = 5.98*1024 kg
T = 5.4*103
s = 90 min.
Problem:
Io, a satellite of Jupiter, has an orbital period of 1.77 days and an orbital
radius of 4.22*105 km. From these data, determine the mass of
Jupiter.
Solution:
- Concepts:
Motion in a central potential, Kepler's third law
- Reasoning:
Two astronomical objects pull each other towards their
common center of mass. Each object accelerates towards the center of mass.
The acceleration of object 1 is a1 = Gm2/R2,
and the acceleration of object 2 is a2 = Gm1/R2.
If each object has velocity perpendicular to the direction of its
acceleration and v12/R1 = a1, v22/R2
= a2, with R1 and R2 being the
distances of object 1 and object 2 from the CM, then both objects orbit
their common CM in circular orbits. If object 1 is much more massive than
object 2, then the CM lies very close to the center of object 1. Then R2
is approximately equal to R and we can write Gm1/R = v22.
If object 2 is in a circular orbit about a much more massive object 1, its
speed is given by this formula. We may write v2 = 2πR/T2,
where T2 is the period of object 2. We then have Gm1/R
= (2πR/T2)2, or T22 = (4π2/Gm1)R3.
- Details of the calculation:
Let object 1 be Jupiter, and object 2 be
Io. Then
T22 = (4π2/Gm1)R3.
m1 = (4π2/GT22)R3.
m1 = 4π2(4.22*108m)3/((6.67*10-11Nm2/kg2)(1.77*24*60*60s)2)
= 1.9*1027kg.
Problem:
The source of the first gravitational wave event observed by the LIGO
collaboration in 2015 has been interpreted as the merger of two black holes in a
binary system, each with a mass of roughly 35 solar masses (implying a radius
for the event horizon of about 100 km for each, if assumed spherical), where a
solar mass is 1.989*1030 kg. A full understanding
requires general relativity, but assume Newtonian mechanics and Newtonian
gravity as a first approximation for the orbital motion. At the peak
amplitude of the detected gravitational wave, its measured frequency indicated
that the two black holes were revolving around the center of mass about 75 times
per second.
What was the approximate separation of the centers for the
two black holes at this point in the merger event?
Solution:
- Concepts:
Kepler's third law, relative motion
- Reasoning:
The problem of two interacting particles in their CM frame
is equivalent to the problem of a fictitious particle of reduced mass μ
moving in a central potential U(r).
- Details of the calculation:
Here U(r) = Gm2/r, F(r) = Gm2/r2,
r = distance between their centers.
μv2/r = Gm2/r2.
v2 = Gm2/(μr). μ = m/2. v2 = G 2m/r.
(2πr/T)2 = G 2m/r. r = [T2 G2m/(4π2)](1/3).
With T = (1/75) s and m = 35*1.989*1030 kg we have r =
3.47*105 m = 347 km.
Problem:
A particle of mass m is released a distance b from a fixed origin of force
that attracts the particle according to the inverse square law F(x) = -k/x2.
Find the time required for the particle to reach the origin. Use this
result to show that, if the Earth were suddenly stopped in its orbit, it would
take approximately 65 days for it to collide with the Sun. Assume
that the Sun is as a fixed point mass and Earth's orbit is circular.
Solution:
- Concepts:
Kepler's third law
- Reasoning:
For a central force F(r) = -k/r2, the closed
orbits are elliptical orbits. All elliptical orbits with the same
semi-major axis have the same period. The elliptical orbit with zero
angular momentum is a straight line. The motion of a particle in this orbit
is in one dimension and with the appropriate orientation of the coordinate
system we have F(x) = -k/x2.
- Details of the calculation:
The period of the motion of a particle
with semi-major axis r can easily be found by considering the circular
orbit.
k/r2 = mv2/r, (2πr/T)2r = k/m,
T2 = 4π2mr3/k.
For the particle in the
problem r = b/2 and the time t0 required to reach the origin is
T/2.
t0 = ½πb(½mb/k)½.
If the Earth were
suddenly stopped in its orbit, its semi-major axis would be halved.
(Tnew/365
days) = (Rnew/R)3/2 = 2-3/2. Tnew
= 129 days.
t0 = Tnew/2 = 64.5 days.We can also
brute-force integrate to find t0.
From energy conservation:
½mv(x)2 = -k/b + k/x = k(b - x)/(xb).
v(x)2 = 2k(b
- x)/(mxb). dt = dx/v(x).
t0 = (½mb/k)½∫b0dx
(x/(b - x))½.
let x = v, b - x = u.
∫b0dx√v/√u
= √(uv)|b0 - ½b∫b0dx/√(vu) = ½b∫0bdx/√(vu)
= ½b∫0bdx/√(bx -x2).
Let X = a + bx + cx2
with c < 0. Then ∫dx/√X = (-c)-½sin-1((-2cx -
b)/(b2 - 4ac)½.
∫0bdx/√(bx -
x2) = sin-1(1) - sin-1(-1) = π.
t0
= ½πb(½mb/k)½.
Energy and angular momentum conservation
Problem:
A comet of mass m approaches the solar system with a
velocity v0, and if it had not been attracted towards the sun, it
would have missed the sun by a distance d. Calculate its minimum distance
z from the sun as it passes through the solar system. Make and state any
reasonable simplifying assumptions.
Solution:
- Concepts:
Conservation of energy and angular momentum
- Reasoning:
For the Kepler problem these conservation laws hold.
Key assumptions: Neglect other planets, assume m << Msun, neglect
relativity.
- Details of the calculation:
At r --> infinity , L = mv0d.
L = constant.
At the distance of closest approach r = z, L = mvmaxz.
mv0d = mvmaxz, vmax = v0d/z.
E = mv02/2 = constant = mvmax2/2
- GMm/z.
Therefore z2 + 2GMz/v02 - d2
= 0, z = (G2M2/v04 + d2)½
- GM/v02.
Problem:
Assume for this problem Earth is a sphere of radius R and mass M. An object
of mass m enters Earth's atmosphere at distance R' > R from Earth's center with
speed v at angle α from the radial direction. Ignoring any friction or air
resistance, at what angle β (from the radial direction) will it hit Earth's
surface?
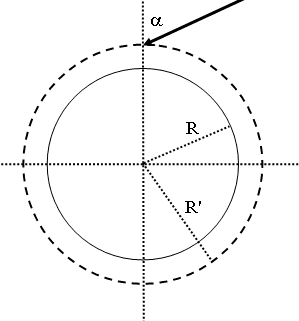
Solution:
- Concepts:
Motion in a central potential, energy and angular
momentum conservation
- Reasoning:
In a central potential energy and angular momentum are conserved.
- Details of the calculation:
At a distance r > R from the center of Earth the object has potential energy
-GMm/r.
Energy conservation:
½mvR'2 - GmM/R' = ½mvR2
- GmM/R,
vR2 = vR'2 + 2(R' - R)GM/(RR').
Angular momentum conservation:
mR'vR'sinα = mRvRsinβ, sinβ = sinα (R'/R)(vR'/vR).
sinβ = (R'/R) sinα vR'/(vR'2 + 2(R' - R)GM/(R'R
))½.
Let R' = aR. Then sinβ = a sinα vR'/(vR'2
+ 2(a - 1)GM/(aR))½.
We need 0 < sinβ < 1 for the object to hit the Earth. If this condition is
not fulfilled than the object reaches its distance of closest approach (sinβ
= 1) and continues in its orbit.
Problem:
A uniform spherical planet of radius a revolves around the sun in
a circular orbit of radius r0 and angular velocity
ω0. It rotates about its axis with
angular velocity Ω0 (period T0)
normal to the plane of the orbit. Due to tides raised on the planet by the
sun, its angular velocity of rotation is decreasing. Find an expression
which gives the orbital radius r as a function of the angular
velocity Ω of rotation and the parameters r0 and T0 at any later or earlier time.
Solution:
- Concepts:
Conservation of angular momentum, Newton's law of gravitation
- Reasoning
No external forces act on the sun-planet system, there are no external
torques. Therefore the total angular momentum of the system is
conserved. Newton's law of gravitation yield a relationship between the
period and the orbital radius of circular orbits for planets orbiting a sun (Kepler's
third law).
- Details of the calculation:
The total angular momentum of the system is the sum of the angular momenta of
the revolution and the rotation. Let the z-direction be the direction
perpendicular to the plane of the orbit. The direction of all angular momenta
is the z-direction.
revolution: Lrev = Mpr2ω
for a spherical orbit.
rotation: Lrot = IΩ = (2/5)Mpa2Ω.
Conservation of angular momentum:
(2/5)Mpa2Ω0 + Mpr02ω0
= (2/5)Mpa2Ω + Mpr2ω.
Newton's law of gravitation:
(2/5)a2Ω0 + r02[GMs/r03]½
= (2/5)a2Ω + r2[GMs/r3]½.
r = (1/GMs)[(2/5)a2[(2π/T0)
- Ω] + [r0GMs]½]2.
Kepler orbits
Problem:
A space station orbits Earth on a circular trajectory. At some moment the
captain decides
to change the trajectory by turning on the rocket engine for a very short period
of time.
During the time the engine was on, it accelerated the station in its direction
of motion. As
a result, the station speed increased by a factor of α. Provide the conditions,
in terms of α,
that the new trajectory is elliptic, parabolic or hyperbolic. Justify your
answers.
Solution:
- Concepts:
Kepler orbits
- Reasoning:
Since the mass of a satellite is negligible compared to
the mass of Earth, assume the CM is the center of Earth. For a single
object moving in a closed orbit in an attractive 1/r potential, the energy E
per unit mass is proportional to inverse of the semi-major axis.
- Details of the calculation:
For the Kepler problem we have:
| E > 0 |
|
|
|
hyperbola |
| E = 0 |
|
|
|
parabola |
| E < 0 |
|
|
|
ellipse |
The energy per unit mass of the satellite in a circular orbit of radius R
is E = -½GM/R, its kinetic energy per unit mass is T = ½GM/R and its
potential energy per unit mass is U = -GM/R. E = T + U.
To put it in a parabolic orbit with E = 0, its kinetic energy per unit mass
at a distance R from the planet has to double. Its speed therefore has to
increase by a factor of √2.
If α > √2 the orbit will be hyperbolic and if 1 < α < √2 the orbit will be
elliptic.
Problem:
For a satellite orbiting a planet, transfer between coplanar circular orbits
can be affected by an elliptic orbit with perigee and apogee distances equal to
the radii of the respective circles as shown in the Figure below. This ellipse
is known as Hohmann transfer orbit.
Assume a satellite is orbiting in a circular orbit of radius rp with
circular orbit speed vc. It is to be transferred into a circular
orbit with radius ra.
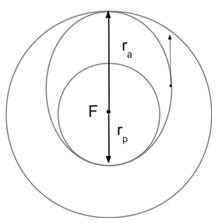
(a) Find EH/Ec, the ratio of the total energies of the
satellite in the Hohmann and the initial circular orbit.
(b) Determine the equation for the ratio of the speeds v/vc as a
function of the ratio of the distances r/rp from the focus for the
Hohman transfer orbit. Evaluate v/vc at r = rp.
Solution:
- Concepts:
Motion in a central potential of the form -α/r, energy
conservation
- Reasoning:
All orbits are Kepler orbits.
- Details of the calculation:
(a) The acceleration of a satellite in a circular orbit of radius r
is a = α/r2 = v2/r.
The speed is v = (α/r)½. T = ½mv2 = ½αm/r = -½U. E
= T + U = ½U = -½mα/r.
We then can write r = αm/(2|E|), |E| = αm/(2r).
This generalizes for an elliptical Kepler orbit to (rmin + rmax)/2
= αm/(2|E|).
Therefore EH/Ec = (2rp)/(rp + ra).
Both EH and Ec are negative, EH is less
negative than Ec.
(b) For the Hohmann orbit , EH = -αm/(rp +
ra) = ½mv2 - αm/r.
½v2 = -α/(rp + ra) + α/r, ½vc2
= α/(2rp), (v/vc)2 = -2rp/(rp
+ ra) + 2rp/r.
v/vc = [-2rp/(rp + ra) + 2rp/r]½.
At r = rp we have v/vc = [-2rp/(rp
+ ra) + 2]½ = [2ra/(rp
+ ra)]½.
To put the satellite in the transfer orbit, its speed has to increase at r = rp.
Problem:
This question is about an elliptical "transfer orbit" from an inner
circular orbit A to an outer circular orbit B. The transfer starts at
point P and is completed at point Q. The transfer orbit is an ellipse
which is tangent to A at point P and tangent to C at point Q.
(a)
Derive a formula for the relationship between v and r for circular orbits.
Is the speed in orbit C greater or less than the speed in orbit A?
(b)
For the transfer, should the satellite speed up or slow down at point P?
(c)
For the transfer, should the satellite speed up or slow down at point Q?
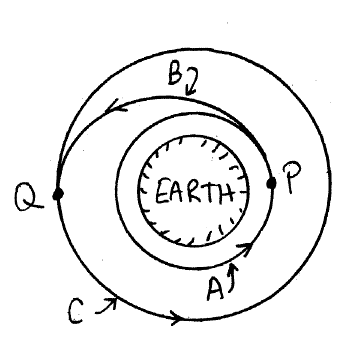
Solution:
- Concepts:
Motion in a potential of the form V(r) = -α/r
- Reasoning:
The satellite moves in the gravitational potential of
Earth. Since the mass of Earth, M, is much greater than the mass of the
satellite, m, we assume that the CM of the system is at the center of
Earth.
- Details of the calculation:
(a) The acceleration of the satellite in
a circular orbit is a = GM/r2 = v2/r. The speed is v
= (GM/r)½. The speed in orbit C is less than the speed in
orbit A.
(b) The transfer orbit is an elliptical orbit. Its semi-major
axis is greater that the radius of orbit A and less than the radius of orbit
B.
From part (a) we have T = ½mv2 = ½GMm/r = -½U. E = T + U =
½U = -½GMm/r.
We then can write r = GMm/(2|E|). This generalizes for an
elliptical Kepler orbit to (rmin + rmax)/2 = GMm/(2|E|).
To increase the semi-major axis we have to decrease |E|, we have to make E
less negative. We have to increase the kinetic energy and therefore speed
the satellite up at point P.
(c) By the same argument, we again have to
increase the speed of the satellite at point Q.
Problem:
In outer space, two small balls of equal unknown masses m and charges +q and
-q are held at rest a distance d0 apart. Then the balls are
simultaneously launched with equal speeds v0 in opposite directions
that are perpendicular to the line connecting the balls. During the subsequent
motion of the balls orbit each other, and their minimum speed is v. Find
the mass m of each ball.

Solution:
- Concepts:
The Kepler problem
- Reasoning:
The problem of two interacting particles in their CM frame is equivalent to
the problem of a fictitious particle of reduced mass μ moving in a central
potential U(r).
The motion is in a plane. Energy E and angular momentum M are
conserved.
- Details of the calculation:
Here U(r) = -α/r, where α = q2/(4πε0), and μ = m/2.
(Neglect gravity.)
Closed orbits in the given potential are ellipses. The fictitious particle
has maximum speed at rmin and minimum speed at rmax.
At these positions dr/dt = 0 and E = M2/(2μr2) - α/r,
The initial conditions specify vmax = v0 at rmin
= d0, since we are told that the particle subsequently slows
down.
Angular momentum conservation:
M = μd02v0 = md0v0 = mrmaxv.
This is one equation but two unknowns, m and rmax.
We need a second equation to eliminate rmax.
Energy conservation:
E = ½μ(2v0)2 -
α/d0 = mv02 - α/d0 = mv2
- α/rmax = mv2 - αv/(v0d0).
m(v2 - v02) = α/d0(v/v0
- 1).
m = q2/(4πε0d0v0(v + v0)).
Problem:
The escape speed from the surface of a slowly rotating airless
spherical planet is vesc. What is the minimum initial speed of a
projectile launched from a pole that allows it to land on the equator?
Note:
For Kepler orbits:
p/r = 1 + e cos(φ - φ0),
p = L2/mα, e = (1 + 2EL2/mα2)½,
L = angular momentum
Solution:
- Concepts:
Kepler orbits
- Reasoning:
After the launch, the particle will have an elliptical (Kepler)
orbit until it lands again.
- Details of the calculation:
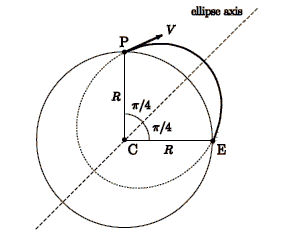
For a Kepler orbit p/r = 1 + e cos(φ - φ0), or r = p/(1
+ e cos(φ - φ0)).
rmax = p/(1 - e), when φ - φ0 = π.
In this expression
p = L2/mα and e = (1 + 2EL2/mα2)½
= (1 + 2Ep/α)½.
α = GMm, L = angular momentum, E = energy, M = mass of planet,
m = mass of
projectile, m << M.
For the given problem p/R = 1 + (1 + 2Ep/α)½ cos(3π/4) = 1 - 2-½(1
+ 2Ep/α)½.
(1 - p/R)2 = ½ + Ep/α, ½ -2p/R + p2/R2 =
Ep/α, 1/(2p) - 2/R + p/R2 = E/α.
To find the minimum energy we differentiate with respect to p and set the result
equal to zero.
-1/(2p2) + R2 = 0, p = R/2½.
Therefore Emin/α = (√2 - 2)/R.
For the Kepler problem
E = ½mv2 - α/R.
(√2 - 2)/R = ½mvmin2/α - R, (√2 - 1)(2GM/R) =
vmin2.
The escape speed vesc for the planet is found by setting ½mvesc2
= GmM/R, vesc = (2GM/R)½.
vmin2 = (√2 - 1)vesc2.
Problem:
A particle of mass m is moving in a central potential of the form V(r) =
-α/r.
(a) What is the total energy of the particle if it is moving in
a circular orbit of radius R? What is its speed?
(b) What is the
energy of the particle if it is moving in an elliptical orbit of semi-major axis
R? What is its speed at r = rmin, the perigee of its orbit?
Solution:
- Concepts:
Kepler orbits, U(r) = -mα/r,
F = -mα/r2
(r/r)
- Reasoning:
The total energy is E = T + U, energy is conserved.
- Details of the calculation:
(a) F = mv2/R = mα/R2.
v = (α/R)1/2. T = ½mv2 = ½αm/R = -½U. E = T + U
= ½U = -½mα/R.
(b) This formula generalizes for an elliptical Kepler
orbit to
R = (rmin + rmax)/2, E = -½αm/((rmin
+ rmax)/2) = -½mα/R.
The speed of the particle at r = rmin
is found from -½mα/R = ½mv2 - αm/rmin.
v2
= -α/(R) + 2α/rmin.
Problem:
Find the maximum time a comet (C) of mass m following a parabolic trajectory
around the Sun (S) can spend within the orbit of the Earth (E). Assume
that the Earth's orbit is circular and in the same plane as that of the comet.
Solution:
- Concepts:
The Kepler problem
- Reasoning:
Both the Earth and the comet move in the central potential
V(r) = -β/r. Let the radius of the circular orbit of the Earth be a. We
need to find the time a comet following a parabolic orbit can spend between
rmin and a.
- Details of the calculation:
The total energy of a particle following
a parabolic orbit is zero.
E = ½mc(dr/dt)2 + Ueff(r)
= 0, Ueff(r) = U(r) + M2/(2mcr2)
= -mcβ/r + M2/(2mcr2).
At r =
rmin we have dr/dt = 0 and mcβ/rmin = M2/(2mcrmin2).
M2 = 2mc2βrmin.
We have found
the relationship between M and rmin.
dr/dt = ((2/m)(E - Ueff(r))½.
The time the comet spend between rmin and a is
t = 2∫rmina
dr/[(2/mc)(mcβ/r - M2/(2mcr2))]½.
t = 2∫rmina dr/[(2/mc)(mcβ/r - mcβrmin/r2)]½.
t = (2/β)½∫rmina rdr/(r - rmin)½.
∫rmina rdr/(r - rmin)½ = (2/3)a3/2(1
+ 2rmin/a)(1 - rmin/a)½.
Let x = rmin/a.
t = C(1 + 2x)(1 - x)½. Let us find an extremum for t.
dt/dx =
2C(1 - x)½ - ½C(1 + 2x)(1 - x)-½ = 0.
2(1 - x) -
½(1 + 2x) = 0. 3x = 3/2, x = ½.
Since for rmin > a the time
t spend within Earth's orbit is zero, the extremum is a maximum.
The
comet following a parabolic orbit spends the maximum time between rmin
and a when rmin = a/2.
Then tmax = (1/β)½(4/3)a3/2.
Since (a3/β)½ = T/2π (Kepler's third law), we have tmax
= 2T/(3π).
tmax = (2*365 days)/(3π) = 77 days.





