Scattering

Definitions

Problem:

A target of Aluminum (A = 27) with an aerial density of 1 mg/cm² is positioned perpendicular to a 0.5 μA beam of deuterons (Z = 1).  If the cross section for producing protons at an angle of 30^o with respect to the beam direction is 15 mb/sr, (1 mb = 10^-27 cm²), how many protons per second will be incident on a 1 cm² detector facing the target at 30^o and 10 cm from the target?

Solution:

• Concepts:
  The cross section
• Reasoning:
  We are given the cross section for producing a proton in a single deuteron - Aluminum nucleus collision.
  We are asked to find the total number of protons hitting a detector per second.
• Details of the calculation:
  If we have not one, but many scattering centers we distinguish the following limiting cases:
  (a)  small beam, big target:
  
  (# of particles scattered into the solid angle dΩ)/s
  = [(# of beam particles)/s] * [(# of target particles)/area ] * σ(Ω)dΩ.
  
  (b)  big beam, small target:
  
  (# of particles scattered into the solid angle dΩ)/s
  = [(# of beam particles)/(area * s)] * (# of target particles) * σ(Ω)dΩ.
  In this  problem we have case (a).
  (# of beam particles)/s = (0.5*10^-6 C/s)/(1.6*10^-19 C) = 3.125*10¹²/s.
  (# of aluminum atoms)/cm² = (1 mg/cm²)/(27*1.6*10^-27 kg) = 2.29*10¹⁹/cm².
  What is dΩ?
  r²dΩ = (10 cm²)dΩ = 1 cm²,  dΩ = 0.01 sr.
  # of protons/s = (3.125*10¹²/s) * (2.29*10¹⁹/cm²) * (15*10^-27 cm²) * 0.01 = 1 * 10⁴/s.

Hard sphere scattering

Problem:

Calculate the differential and total scattering cross section for scattering a particle off a fixed, "hard" sphere of radius R.

Solution:

• Concepts:
  The scattering cross section, scattering from a spherically symmetric potential
• Reasoning:
  The potential has spherical symmetry, V(r) = ∞, r < R;  V(r) = 0, r >R.
• Details of the calculation:
  For scattering off a central potential we have σ(θ) = |(b/sinθ)(db/dθ)|,  θ = π - 2φ₀.
  
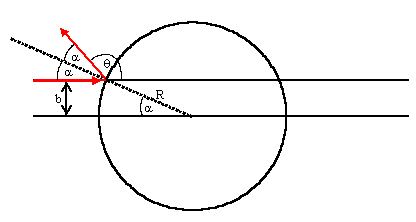
  Referring to the figure above we have
  b/R = sinα
  θ = π - 2α.
  α = (π - θ)/2.
  b = Rsin(π/2 - θ/2) = Rcos(θ/2).
  db/dθ = (R/2)sin(θ/2).
  σ(θ) = (b/sinθ)((R/2)sin(θ/2) = R²cos(θ/2)sin(θ/2)/(2sinθ) = R²/4.
  σ_total = ∫σ(θ)dΩ, = ∫∫σ(θ)sin(θ)dθdΦ = πR² = total elastic scattering cross section.

Problem:

Solution:

• Concepts:
  Conservation of energy and momentum
• Reasoning:
  In the elastic collision kinetic energy and momentum are conserved.
• Details of the calculation:
  Let disk A initially move in the x direction. 
   
  The in the CM frame the initial velocity of disk A is 5 m/s i and the initial velocity of disk B is -5 m/s i. 
  After the collision disk A has velocity components v_xA = -5 m/s cosθ, v_yA = 5 m/s sinθ, and disk B has velocity components v_xB = 5 m/s cosθ, v_yB = -5 m/s sinθ.
  In the lab frame v_A = 5 m/s (1 - cosθ) i + 5 m/s sinθ j,
  and v_B = 5 m/s (1 + cosθ) i - 5 m/s sinθ j.
  v_A² = 25 m²/s² = 25 m²/s² [(1 - cosθ)² + sin²θ].
  2 - 2cosθ = 1, θ = 60^o.
  Impact parameter b:  b = 2R sin30^o = R.

Problem:

Consider the perfectly elastic scattering of a hard sphere of mass m and initial velocity v₀ against a stationary hard sphere of mass M.  The sum of the radii of the two spheres is D.
(a)  Compute the energy lost by the small mass in the collision in the lab frame as a function of the scattering angle θ in the center of mass frame.
(b)  Compute the probability P(θ)dθ of scattering through an angle θ in the center of mass frame, assuming that the particles m in the incident beam are uniformly distributed across a cross section of the beam.  Find the differential scattering cross section σ(θ), and show that your expression integrates to the known total hard sphere cross section πD².
(c)  Use the results of parts (a) and (b) to compute the average energy loss per collision.  For what value of m/M does the average energy loss maximize?

Solution:

• Concepts:
  Elastic scattering, energy and momentum conservation, frame transformations
• Reasoning:
  In the elastic collision kinetic energy and momentum are conserved.  A frame transformation is necessary because the energy lost by the small mass in the lab frame is given in terms of the scattering angle in the CM frame.
• Details of the calculation:
  (a)  The CM frame moves with respect to the laboratory frame with speed V.
  Before the collisions: m(v₀ - V) =  MV.  Therefore: V = mv₀/((m + M).
  In the CM frame m has speed (v₀ - V) = Mv₀/(m + M) = v' before and after the collision.
  In the lab frame the speed of m after the collision is v.
  
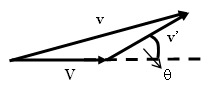
  v² = v'² + V² + 2v'Vcosθ = v₀²(m² + M² + 2mMcosθ)/(m + M)²
  = v₀²(1 - 2mM(1 - cosθ)/(m + M)²).
  (v² - v₀²)/v₀² = ∆E/E = -2mM(1 - cosθ)/(m + M)²).
  ∆E = -v₀²m²M(1 - cosθ)/(m + M)²) is the energy lost by the small mass in the collision in the lab frame as a function of the scattering angle θ in the center of mass frame.
  (b)  Let b be the impact parameter.
  
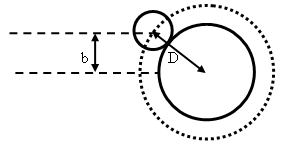
  For particles which collide, P(b)db = 2πbdb/(πD²) is the probability of a collision with impact parameter between b and b + db.
  
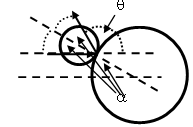
  θ = π - 2α.  b = Dsinα.
  The relationship between the impact parameter and the scattering angle is
  b = Dsin(π/2 - θ/2) = Dcos(θ/2),  db/dθ  = -(D/2)sin(θ/2).
  P(θ)dθ   = P(b)|db/dθ|dθ  =  2b|db/dθ|dθ/D² = cos(θ/2)sin(θ/2)dθ = ½sinθdθ.
  ∫₀^πP(θ)dθ = 1.
  σ(θ) =|(b/sinθ)(db/dθ)| = ½D²cos(θ/2)sin(θ/2)/sinθ.
  σ(θ) 2π sinθ dθ = πD²cos(θ/2)sin(θ/2)dθ = πD² P(θ)dθ.
  ∫₀^π σ(θ) 2π sinθ dθ = πD².
  (c)  average energy loss = ∫₀^π∆E(θ) P(θ)dθ
  = (½v₀²m²M/(m + M)²) ∫₀^π(1 - cosθ)sinθ dθ = v₀²m²M/(m + M)²
  = v₀²m(m/M)/(m/M + 1)².
  d(x/(x +1)²)/dx = 0 for x = 1.
  The average energy loss maximizes for m/M = 1. The average energy loss then equals ½ of the initial kinetic energy.

Scattering by a 1/rⁿ potential

Problem:

A particle of mass m moves under a central repulsive force F(r)  =  km/r³.   At its distance of closest approach r₀ it has speed v₀.
(a)  Find the orbital equation r(θ) for the particle motion, evaluating constants in terms of r₀ and v₀.
(b)  Find the impact parameter and the total angular deflection, assuming the particle approaches from large r.
(c)  Sketch the particle trajectory, indicating the impact parameter and total deflection calculated in part (b).

Solution:

• Concepts:
  Motion in a central potential, F = f(r)(r/r), f(r) = -dU/dr, impact parameter b (M = mbv_inf)
  For motion under the influence of a central force E and M are conserved.
  M = mr²φ, E = ½m(dr/dt)² + U_eff(r),  U_eff(r) = U(r) + M²/(2mr²).
  The equation that relates the orbit to the force is
  (M²u²/m)(d²u/dφ² + u) = -f(u),  where  u = 1/r.
• Reasoning:
  We are given the force and are asked to find the equation of the orbit.  We are then asked to find a relationship between the impact parameter and the total deflection.
• Details of the calculation:
  (a)  f(u) = kmu³, d²u/dφ² + u = -(km²/M²)u,  d²u/dφ² + (1 + km²/M²)u = 0, 
  u = A sin(Bφ + C).
  B² = (1 + km²/M²),  M = mbv_inf = mr₀v₀,  B² = (1 + k/(r₀v₀)²).
  Let u = 0 at φ = 0, then C = 0.
  At the distance of closest approach φ = φ₀, r = r₀ = r_min, u = u_max.
  1/r₀ = A sin(Bφ₀) = A sin(π/2),  Bφ₀ = π/2,  A = 1/r₀, 
  1/r = (1/r₀)sin((1 + k/(r₀v₀)²)^½φ)
  (b)  Bφ₀ = π/2,  φ₀ = π/(2B).  We need φ₀ in terms of the impact parameter b.
  From energy conservation we have E = ½mv_inf² = ½mv₀² + km/2r₀², 
  v_inf² = v₀² + k/r₀².
  b = r₀v₀/v_inf,  b² = (r₀v₀)²/(v₀² + k/r₀²) = r₀²/B².   b = r₀/B is the impact parameter.
  φ₀ = πb/(2r₀).  θ = π - 2φ₀ is the deflection angle.
  (c)  For example, pick b = r₀/2,  then φ₀ = π/4,  θ = π/2.
  

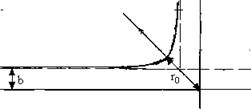
Problem:

A fixed force center scatters a particle of mass m and initial velocity u₀ according to the force law f(r) = k/r³.  Determine the differential scattering cross section.

Solution:

• Concepts:
  A particle moving in a central potential
  U = U(r),  F = f(r)(r/r), f(r) = (-∂U/∂r).  U = k/(2r²).  E > 0 for scattering.
• Reasoning:
  We are asked to find the differential scattering cross section for a particle being scattered by a central force.
• Details of the calculation:
  f_r = -∂U/∂r = k/r³.
  σ(θ) = |(b/sinθ)(db/dθ)|  θ = π - 2φ₀ if k > 0.
  We need to find θ as a function of b.
  U = k/(2r²),  U(u) = ku²/2,  u = 1/r.
  
  φ₀ = ∫₀^u_max bdu/(1 - b²u² - ku²/(2E))^½
  for motion in a central potential.
  u_max = (E/(b²E + k/2))^½.
  
  Let k > 0, repulsive potential:
  φ₀ = b(b² + k/(2E))^-½∫₀¹ du'/(1 - u'²)^½,  u' = (b² + ku/(2E))^½.
  φ₀ = b(b² + k/(2E))^-½sin^-1(1) = (bπ/2)/(b² + k/(2E))^½
  since ∫dx/(a² - x²)^½ = sin^-1(x/a).
  
  θ = π - πb/(b² + k/(2E))^½,  (π - θ)² = (πb)²/(b² + k/(2E)),
  b² = [k/(2E)](π - θ)²/[θ(2π - θ)].
  db²/dθ  = 2bdb/dθ  = -(k/E)π²(π - θ)/[θ²(2π - θ)²].
  σ(θ) = (k/(2E))π²(π - θ)/[θ²(2π - θ)²sinθ].
  
  Let k < 0, attractive potential:
  If b²E < |k/2| we find no solution for u_max, there is no turning point, the particle spirals into the origin.  Its angular velocity increases beyond any limit, such that mr²dφ/dt = M stays constant.
  If b²E > |k/2| we have φ₀ = (bπ/2)/(b² + (k/(2E)))^½ > π/2.
  φ₀ may be much larger than 2π, the particle may turn around the force center several times.

Problem:

Two particles of mass m are moving in the x-y plane.  The inter-particle potential energy is U(r₁ - r₂) = U₀/|r₁ - r₂|² with U₀ > 0.  The initial conditions are
r₁(t = 0) = (-∞, -y₀),  r₂(t = 0) = (∞, y₀), and p₁(t = 0) = (p₀, 0),  p₂(t = 0) = (-p₀, 0),
with p₀ > 0.  What is the distance of closest approach of the two particles?

Solution:

• Concepts:
  Motion in a central potential.
• Reasoning:
  The problem of the relative motion of two interacting masses m₁ and m₂ can be solved by solving for the motion of one fictitious particle of reduced mass μ in a central field.
• Details of the calculation:
  For motion in a central field energy E and angular momentum M are conserved.
  E = p₀²/2μ = p₀²/m,  M = 2y₀p₀.
  At the distance of closest approach: E = p_c²/m + U₀/r_c²,  M = r_cp_c.  Here r_c = |r₁ - r₂|_c.
  Then p_c = M/r_c, E = M²/(mr_c²) + U₀/r_c² = 4y₀²p₀²/(mr_c²) + U₀/r_c² = p₀²/m.
  r_c² = 4y₀² + mU₀/p₀².
  The distance of closest approach is r_c = (4y₀² + mU₀/p₀²)^1/2.

Problem:

A point like comet of mass m approaches a sun with mass M and Radius R with speed v_∞ > 0.  What is the total cross section for the comet to crash on the sun?

Solution:

• Concepts:
  Motion in a central potential.
  Reasoning:
  The comet has a hyperbolic orbit.  Energy E and angular momentum L are conserved, the motion is in a plane.
  L = mbv_∞ = mr_cv_c, where r_c is the distance of closest approach, and v_c is the speed at r_c.
  The potential energy of the comet is U(r) = -GMm/r.  If r_c < R, the comet will crash onto the sun.
  We find the relationship between r_c and b, and find the largest impact parameter b_max for which r_c < R.
  The cross section for crashing onto the sun is σ = πb_max².
• Details of the calculation:
  For motion in a central field energy E and angular momentum L are conserved.
  E = ½mv_∞² = ½mv_c² - GMm/r_c.  v_c² = v_∞² + 2GM/r_c.
  L = mbv_∞ = mr_cv_c,  v_∞ = r_cv_c/b.
  b = r_cv_c/v_∞ = r_c(1 + 2GM/(r_cv_∞²))^½.  b_max = R(1 + 2GM/(Rv_∞²))^½.
  σ = πR²(1 + 2GM/(Rv_∞²))^½.

Problem:

In frame B particles with speed v_B << c are scattered uniformly in all directions.  Frame B moves with velocity v₀ k (v₀ << c) with respect to frame A.
(a)  If the scattering angle of a particle in frame B is θ_B, what is the corresponding scattering angle θ_A in frame A, and what is the speed of the particle v_A?
(b)  Given that dσ/dΩ_B = K = constant, derive an expression for dσ/dΩ_A in terms of v₀, v_B, v_A,  and θ_A.
(c)  Show that when v₀ > v_B, there is a maximum angle θ_{A_max}, which is given by sinθ_{A_max} = v_B/v₀.
(d)  What happens to  dσ/dΩ_A near θ_{A_max}?

Solution:

• Concepts:
  Frame transformations
• Reasoning:
  
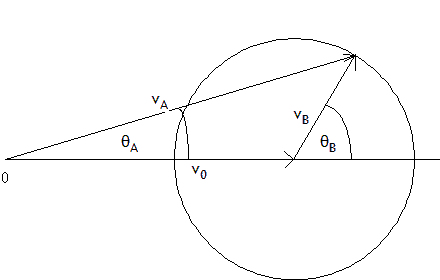
  Using the figure and trigonometry, we can find v_A and θ_A in terms of v₀, v_B, and θ_B.
• Details of the calculation:
  (a)  v_A = v₀ + v_B.
  v_Acosθ_A = v_Bcosθ_B + v₀,   v_Asinθ_A = v_Bsinθ_B,  or  tanθ_A = sinθ_B/(cosθ_B + γ).
  Here γ = v₀/v_B.
  θ_A = tan^-1(sinθ_B/(cosθ_B + γ)).
  v_A² = v₀² + v'_B² +2v₀v_Bcosθ_B.
  
  (b)  σ(θ_A,φ_A)dΩ_A = σ(θ_B,φ_B)dΩ. 
  σ(θ_A,φ_A) sinθ_A dθ_A = σ(θ_B,φ_B) sinθ_B dθ_B.  (The angle φ is the same in the CM and laboratory frame.)
  We can therefore write
  σ(θ_A,φ_A) = σ(θ_B,φ_B) sinθ_B dθ_B/(sinθ_A dθ_A) = σ(θ_B,φ_B) dcosθ_B/dcosθ_A.
  We have tanθ_A = sinθ_B/(cosθ_B + γ).  Somehow we have to use this to evaluate dcosθ_B/dcosθ_A.
  Use tanθ_A = (1/cos²θ_A - 1)^½  = sinθ_B/(cosθ_B + γ).
  Let x = cosθ_B and y = cosθ_A.
  tanθ_A = (1/y² - 1)^½ = (1 - y²)^½/y = (1 - x²)^½/(x + γ).
  y² = (x + γ)²/(1 + 2xγ + γ²).
  dy/dx = (1 + γx)/1 + γ² + 2γx)^3/2.
  This then yields
  σ(θ_A,φ_A) = σ(θ_B,φ_B) (1 + γ² + 2γcosθ_B)^3/2/|1 + γcosθ_B|.
  
  (c)  When v₀ > v_B, γ = v₀/v_B > 1.
  d(tanθ_A)/dθ_B =   (cos²θ_B + γcosθ_B + sin²θ_B)/(cosθ_B + γ)²
  = (1 + γcosθ_B)/(cosθ_B + γ)² = 0 --> cosθ_B = -1/γ.
  tanθ_A has a maximum when cosθ_B = -1/γ.
  tanθ_A-max = (1 - 1/γ²)^½/(γ - 1/γ) = (1/γ)/(1 - 1/γ²)^½.
  1 + cot²θ_A-max = 1/sin²θ_A-max = γ².  sinθ_A-max = 1/γ.
  
  We can also just work from the figure.  θ_A has its maximum value when v_A is tangential to the circle.  Then the angle between v_A and v_B is a right angle, and  sinθ_A-max = v_B/v₀ = 1/γ.
  
  (d)  |1 + γcosθ_B|  --> 0, therefore  σ(θ_A,φ_A) --> ∞.