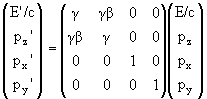Decay including massless partners
Problem:
A particle of rest mass M disintegrates at rest into a particle of rest mass
m1, a particle of rest mass m2, and a high-energy photon
(a gamma ray). Find the maximum possible energy of the gamma ray in the rest
frame of the initial particle of rest mass M.
Solution:
- Concepts:
Relativistic "collisions", energy and momentum conservation
- Reasoning:
The decay of a particle is a relativistic problem. In relativistic
"collisions" energy and momentum are always conserved.
- Details of the calculation:
The γ-ray will have its maximum possible
energy if after the disintegration the two particles have no relative
kinetic energy.
Energy conservation: Mc2 = (m2c4 + p2c2)½
+ Eγmax.
Here m = m1 + m2.
Momentum conservation: pc = Eγmax.
Combine: Eγmax = ½Mc2 - ½m2c2/M
= ½(M - (m1 + m2)2/M)c2.
If m = M, then Eγmax = 0.
Problem:
A π0 meson decays into two γ-rays while at rest or in flight:
π0 --> γ + γ.
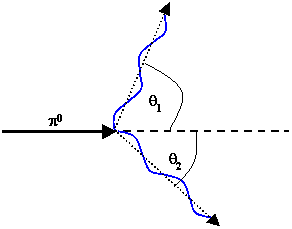
(a) If the decaying π0 has velocity
v and rest mass mπ
, and the γ-ray is emitted at an angle θ with respect to the original direction
of the π0, find the γ-ray energy as a function of mπ,
v,
and θ.
(b) What is the maximum and minimum energy an emitted γ-ray can
have, and at what emission angles do these occur?
Solution:
- Concepts:
Relativistic "collisions", energy and momentum conservation
- Reasoning:
The decay of a particle is a relativistic problem. In
relativistic "collisions" energy and momentum are always conserved.
- Details of the calculation:
(a) In the laboratory, we have from
energy and momentum conservation:
γmc2 = hf1 + hf2,
γmv = hf1cosθ1/c + hf2cosθ2/c,
hf1sinθ1/c = hf2sinθ2/c. Here m
is the mass of the π0.
We want to find hf1 as a
function of θ1.
Eliminate cosθ2: (γmv -hf1cosθ1/c)2
= (hf2/c)2(1-sin2θ2) = (hf2/c)2
- (hf1/c)2sin2θ1.
Eliminate
hf2: (γmv -hf1cosθ1/c)2 + (hf1/c)2sin2θ1
= (hf2/c)2 = ( γmc- hf1/c)2.
Write out all the terms: γ2m2(v2 - c2)
- 2γmhf1((v/c)cosθ1 - 1) = 0.
hf1 = mc2/[2γ(1
- (v/c)cosθ1)].
(b) hf1max = mc2/[2γ(1
- (v/c))]. cosθ1 = 1, θ1 = 0,
Emax =
(mc2/2)[(1 + v/c)/(1 - v/c)]½.
hf1min
= mc2/[2γ(1 + (v/c))]. cosθ1 = -1, θ1 =
180,
Emin = (mc2/2)[(1 - v/c)/(1 + v/c)]½.
In the rest frame of the π0 the two γ's are emitted with
energies (mc2/2) in the forward and backward directions. In the
lab frame they are Doppler shifted.
Problem:
A beam of π+ particles (mπ+ = 140
MeV/c2) is accelerated, so it has momentum pπ+ = 2 GeV/c
in the laboratory frame. A π+ particle decays into a positive
muon (mμ = 105 MeV/c2) and a muon neutrino (mνμ
= 0 MeV/c2) .
(a) What is the energy of the muon in
the rest frame of the π+ particles?
(b) What is the energy
of the muon in the laboratory frame if it is found traveling in the beam
direction?
(c) What is the energy of the muon in the laboratory frame
if it is found traveling at 0.25 rad with respect to the beam direction?
Solution:
- Concepts:
Relativistic "collisions", energy and momentum conservation
- Reasoning:
The decay of a particle is a relativistic problem. In
relativistic "collisions" energy and momentum are always conserved.
- Details of the calculation:
(a) Energy conservation: mπ+c2
= (mμ2c4 + pμ2c2)½
+ Eν, Eν = pc.
Momentum conservation: pμ
= p.
Combine: (mπ+c2 - En)2
= mπ+2c4 + Eν2 - 2mπ+c2Eν
= mμ+2c4 + Eν2.
Eν = ½mπ+c2 - ½mμ2c2/mπ+.
Eμ = mπ+c2 - Eν = ½mπ+c2
+ ½ mμ2c2/ mπ+ = ½(140 +
1052/140) MeV = 109.375 MeV.
pμ = ½(140 - 1052/140)
MeV/c = 30.625 MeV/c.
(b) The rest frame of the mπ+ moves
with speed v with respect to the lab frame. Let the direction be the
z-direction.
pπ+ = 2 GeV/c. γmv = 2 GeV/c. γv = c*2 GeV/mc2
= c*2000/140 = a*c.
v2 = c2a2/(1 + a2),
v = 0.99756 c. β = 0.99756. γ = (1 + a2)½ = 14.32.
We can now find the energy Eμ' of the muon in the laboratory
frame.
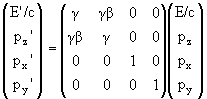
pz = pμ, Eμ' = γEμ + γvpμ
= 2003.8 MeV.
(c) Now pz = pμcos(0.25). Eμ'
= γEμ + γvpμcos(0.25) = 1990.2 MeV
Problem:
Cs55137 is a common laboratory
radioactive source of electrons and gamma rays. Eight percent of the time Cs55137 beta
decays to the ground state of Ba56137.
The net atomic mass difference between the two isotopes is 1.18 MeV/c2. A 180 degree spectrometer is used to measure the beta decay
spectrum. The spectrometer has a
radius R = 3.8 cm.

(a)
Write down the reaction for the beta decay.
(b) Calculate the maximum momentum of the beta decay electron/positron.
Express the result in MeV/c.
(c) What is the vector direction of the spectrometer magnetic field relative
to the drawing?
(d) What is the magnetic field setting of the spectrometer for the maximum
energy of the electron/positron to arrive at the detector?
Provide a numerical answer with units.
Solution:
- Concepts:
Relativistic
"collisions", energy and momentum conservation, motion of a charged
particle in a magnetic field
- Reasoning:
The decay of a
particle is a relativistic problem. In relativistic "collisions" energy and
momentum are always conserved.
- Details of the calculation:
(a) Cs55137
--> Ba56137
+ e- + ν
(ν = anti neutrino)
(b) The source
is at rest. If we assume the antineutrino is massless then the electron
has the maximum energy if the energy of the antineutrino is zero.
If the antineutrino has mass, then the electron has the maximum energy if
the Ba nucleus and the antineutrino have no relative kinetic energy.
Since the mass of the antineutrino is then extremely small, we can
neglect it compared to the mass of the Ba nucleus.
Let M1 be the mass of the Cs nucleus and M2
be the mass of the Ba nucleus.
M1c2 = (M22c4
+ p22c2)½ + (me2c4
+ pe2c2)½ (energy conservation)
p22 = pe2
= p2 (momentum conservation)
The mass of the Ba nucleus is much greater than the mass of
the electron. If we neglect the
recoil of the Ba nucleus (M22c4 >> p2c2)
then
M1c2 - M2c2 =
(me2c4 + p2c2)½
The maximum momentum of the electron is then given by
p2c2 = (M1c2 -
M2c2)2 - me2c4
= (1.18 MeV)2 - (0.511MeV)2
pc = 1.064 MeV
(c) The field
points into the page.
(d) R = p/(qB)
B = 1.064* 106 eV * (1.6 *10-19 J/eV)/[
1.6 *10-19 C * 0.038 m * 3*108 m/s] =
9.33*10-2 T
Problem:
A free atomic nucleus at rest with mass M makes a transition from excited to
ground state by emitting a γ-ray photon.
(a) Find the energy of the γ ray photon and the kinetic energy of the recoil
nucleus if the excitation energy was ΔE.
(b) Calculate the recoil energy of the 191Ir nucleus if the
excitation energy ΔE = 129 keV.
Solution:
- Concepts:
Relativistic dynamics
- Reasoning:
The decay of a particle is a relativistic problem. In relativistic
"collisions" energy and momentum are always conserved.
- Details of the calculation:
Let M be mass of the excited nucleus and m the mass of the de-excited
nucleus.
(a) energy conservation: Mc2 = γmc2 + hν (1)
momentum conservation: hν/c = γmu (2)
ΔE = (M - m)c2 (3)
Rewriting (1): Mc2 - hν = γmc2
Squaring: M2c4 + h2ν2 - 2Mc2hν
= γ2m2c4
Rewriting and substituting (2) and (3): -2Mhν = γ2m2c2
- M2c2 - h2ν2/c2
= γ2m2c2 - M2c2 - γ2m2u2.
= γ2m2(c2 - u2) - M2c2
= m2c2 - M2c2.
2Mhν = (m - M)(m + M)c2 = ΔE (m + M).
Rewriting:
Photon energy: hν = ΔE (m + M)/(2M) = ΔE (m - M + M
+ M)/(2M)
= ΔE(1 - ΔE /(2Mc2)).
Kinetic energy of the recoil nucleus: T = (ΔE)2 /(2Mc2).
(b) The mass of the 191Ir nucleus is ~ 1.67*10-27 kg,
Mc2 ~ 1.79*105 MeV.
T = (129 keV)2/(3.59*108 keV) = 4.64*10-5
keV = 46.4 meV.
Problem:
The question of the proton stability is one of the center questions of Grand
Unification theories. The present experimental limit of the proton lifetime
from the Super Kamiokande experiment is τp > 1.6·1033 y.
More sensitive experiments have been proposed. One of the possible proton
decay modes is p --> e+ + π0, followed by the decay of the
neutral pion into two photons: π0 --> γ + γ
Assume that the protons are at rest.
(a) What is average flight distance of the neutral pion before its decay?
(b) What are the maximum and minimum energies the photons can have?
Mp = 938.27 MeV
Mπ = 134.98 MeV
Me = 0.511 MeV
τπ = 8.4·10-17 s
Solution:
- Concepts:
Relativistic "collisions", energy and momentum conservation
- Reasoning:
The decay of a particle is a relativistic problem. In relativistic
"collisions" energy and momentum are always conserved.
- Details of the calculation:
p --> e+ + π0:
Momentum conservation: γπβπMπ = γeβeMe.
(γπ2 - 1)Mπ2 = (γe2
- 1)Me2.
γe2 = (γπ2 - 1)Mπ2/Me2
+ 1.
Energy conservation: Mp = γπMπ + γeMe.
Combining: Mp2 + (γπMπ)2
- 2MpγπMπ = γe2Me2
= (γπ2 - 1)Mπ2 + Me2.
γπ = (Mp2 + Mπ2 - Me2)/(
2MpMπ ) = 3.55, βπ = ((γπ2
- 1)/ γπ2)½ = 0.96.
Average flight distance: <x> = vπγπτπ = cγπβπτπ
= 85.2 nm in the lab frame.
(b) Maximum and minimum energies the photons can have:
Emax = (Mπc2/2)[(1 + vπ/c)/(1 -
vπ/c)]½ = 468.1 MeV.
Emin = (Mπc2/2)[(1 - vπ/c)/(1 +
vπ/c)]½ = 9.7 MeV.
Problem:
A pion (π) decays at rest into a muon (μ) and a neutrino (ν). In terms of
the masses mπ and mμ (use the approximation mν
= 0), find:
(a) the momentum, energy, and velocity of the outgoing muon.
(b) In the rest frame of the outgoing muon, what is the energy of the neutrino?
What was the initial velocity of the pion in this frame?
Solution:
- Concepts:
Conservation of energy and momentum, the Lorentz transformation
- Reasoning:
The decay of a particle is a relativistic problem. In relativistic
"collisions" energy and momentum are always conserved.
- Details of the calculation:
(a) In the rest frame of the decaying pion let the muon move in the
positive x-direction and the neutrino move in the negative x-direction.
Energy conservation: Mpc2 = (Mμ2c4
+ p2c2)½ + Eν.
Here p is the momentum of the muon.
Momentum conservation: pc = Eν.
Combine: (Mpc2 - Eν)2 = Mp2c4
+ Eν2 - 2Mpc2Eν = Mμ2c4
+ Eν2
Eν = ½Mpc2 - ½Mμ2c2/Mp
= (c2/(2Mp))(Mp2 - Mμ2)
p = Eν/c = (c/(2Mp))(Mp2 - Mμ2)
= momentum of the outgoing muon.
Eμ = Mpc2 - Eν = (c2/(2Mp))(Mp2
+ Mμ2) = energy of the outgoing muon.
v = pc2/Eμ = c(Mp2 - Mμ2)/
(Mp2 + Mμ2) = speed of the
outgoing muon.
(b) The muon moves with respect to the original rest frame of the pion with
speed v.
The original speed of the pion in the muon's rest frame therefore was v. It
was moving in the negative x-direction. The relative speed of the two frames
is v.
β = v/c = (Mp2 - Mμ2)/ (Mp2
+ Mμ2)
γ = (1 - v2/c2)-½ = (Mp2
+ Mμ2)/(2MpMμ)
Lorentz transformation of the (p0,p) = (Eν/c,
-i Eν/c) 4-vector from the original rest frame of the pion
to the rest frame of the muon:
Eν'/c = γEν/c + βγ Eν/c = (Mp/Mμ)Eν
is the energy of the neutrino in the rest frame of the muon.
Problem:
A pion (mass Mp) decays into a muon (mass Mμ) and a
neutrino (massless).
(a) Find the kinetic energy of the muon in the
rest frame of the pion.
(b) The muon is unstable, with a lifetime τ1
in the pion's rest frame. Find the lifetime t0 of the muon in
its own rest frame.
Solution:
- Concepts:
Relativistic "collisions", energy and momentum conservation
- Reasoning:
The decay of a particle is a relativistic problem. In
relativistic "collisions" energy and momentum are always conserved.
- Details of the calculation:
(a) Energy conservation: Mpc2
= (Mμ2c4 + p2c2)1/2
+ En.
Here p is the momentum of the muon.
Momentum
conservation: pc = En.
Combine: (Mpc2
- En)2 = Mp2c4 + En2
- 2Mpc2En = Mμ2c4
+ En2.
En = ½Mpc2
- ½Mμ2c2/Mp.
Eμ =
Mpc2 - En = ½Mpc2 + ½
Mμ2c2/ Mp.
T = Eμ
- Mμc2 = (Mp - Mμ)2c2/(2Mp).
(b) τ0 = τ1/γ. We need to find γ.
T = (Mp
- Mμ)2c2/(2Mp) = (γ - 1)Mμc2.
(γ - 1) = (Mp - Mμ)2/(2MμMp),
γ = ( Mp2 + Mμ2)(/2MμMp),
τ0 = τ12MμMp/( Mp2
+ Mμ2).
Problem:
An excited nucleus of 57Fe formed by the radioactive decay of
57Co emits a gamma ray of 1.44 *104 eV. In the process,
there is conservation of energy and m0c2 = γma0c2
+ hf, where m0c2 is the initial mass of the nucleus
and ma0c2 is its mass after the emission of the gamma ray.
There is also conservation of momentum, hf/c = γma0u, where u is the
recoil velocity of the iron nucleus. The energy released by the reaction
is Er = (m0 - ma0)c2.
(a)
Show that hf = Er(m0 + ma0)/(2m0)
= (1 - Er/(2m0c2))Er.
Thus hf < Er:
part of Er goes to the photon, and the other part supplies kinetic
energy to the recoiling nucleus.
(b) Set m0 = 57*1.7*10-27
kg, and show that Er/(2m0c2)) ~ 1.3*10-7.
Thus the fraction of the available energy Er that appears as recoil
is small.
(c) Moessbauer discovered in 1958 that, with solid iron, a
significant fraction of the atoms recoil as if they were locked rigidly to the
rest of the solid. This is the Moessbauer effect. If the sample has a
mass of 1 gram, by what fraction is the gamma ray energy shifted in the recoil
process?
(d) A sample of normal 57Fe absorbs gamma rays
of 14.4 keV by the inverse recoilless process much more strongly than it absorbs
gamma rays of any nearby energy. The excited nuclei thus formed reemit
14.4 keV radiation in random directions some time later. This is resonant
scattering. If a sample of activated 57Fe moves in the
direction of a sample of normal 57Fe, what must be the value of the
velocity v that will shift the frequency of the gamma rays, as seen by the
normal nuclei, by 3 parts in 1013? This is one line width.
(e) A Doppler shift in the gamma ray results in a much lower
absorption by a nucleus if the shift is of the order of one line width or more.
What happens to the counting rate of a gamma-ray detector placed behind the
sample of normal 57Fe when the source of activated Fe moves
(i) toward the normal 57Fe,
(ii) away from it?
(f) If a 14.4 keV gamma ray travels 22.5 meters vertically upward, by
what fraction will its energy decrease?
[Gravitation redshift, a thought
experiment: Suppose a particle of rest mass m is dropped from the top of a
tower and falls freely with acceleration g. It reaches the ground with a
velocity v = (2gh)1/2, so its total energy E, as measured by an
observer at the foot of the tower is E = mc2 + ½mv2 + O(v4)
= mc2 + mgh + O(v4).
Suppose an observer has some
magical method of converting all this energy into a photon of the same energy.
Upon its arrival at the top of the tower with energy E the photon is again
magically changed into a particle of rest mass m' = E'/c. Energy conservation
requires that m' = m.
Therefore E'/E = mc2/(mc2
+ mgh + O(v4)) = (1 + gh/c2 + O(v4))-1
= 1 - gh/c2 + O(v4).]
(g) A normal 57Fe
absorber located at this height must move in what direction and at what speed in
order for resonant scattering to occur?
Solution:
- Concepts:
Relativistic decay, energy and momentum conservation, the
Doppler shift
- Reasoning:
The decay of a particle is a relativistic problem. In
relativistic "collisions" energy and momentum are always conserved.
The
Doppler shift can compensate for the gravitational redshift to produce
optimum absorption.
- Details of the calculation:
(a) energy conservation: m0c2
= γma0c2 + hf. (1)
momentum conservation: hf/c
= γma0u. (2)
Define: Er = (m0
- ma0)c2. (3)
Show:
hf = Er(m0 - ma0)/(2m0).
m0c2
- hf = γma0c2.
(1)
m02c4
+ h2f2 - 2m0c2hf = γ2ma02c4.
square (1)
-2m0hf = γ2ma02c2
- m02c2 - h2f2/c2
= γ2ma02c2 - m02c2
- γ2ma02u2
= γ2ma02(c2
- u2) - m02c2 = ma02c2
- m02c2. insert (2)
2m0hf
= (ma0 - m0)(ma0 + m0)c2
= Er(ma0 + m0). rearrange
hf = Er(ma0
+ m0)/(2m0) = Er(ma0 - m0
+ m0 + m0)/(2m0) = Er(1 -
Er/(2m0c2)).
(b) Set m0
= 57*1.7*10-27 kg, hf = 1.44*104 eV.
Er
- Er2/(2m0c2)) - hf = 0. Er2
- 2m0c2Er + 2m0c2hf =
0.
Er = m0c2 - ((m0c2)2
- 2m0c2hf)1/2.
m0c2
= 8.72*10-9 J, hf = 2.3*10-15 J, Er = 2.3
*10-15 J.
Er/(2m0c2) ~ 1.3*10-7.
(c) If m0 = 10-3 kg, then m0c2
= 9*1013 J, Er/(2m0c2) ~
1.27*10-29.
The fraction that appears as recoil energy is now
negligible.
The gamma ray energy is now hf = Er. It has
increased by Er2/(2m0c2)) =
1.3*10-7 Er.
Δf/f = 1.3*10-7.
(d) We want Δf/f = 3*10-13.
Δf/f = (f' - f)/f = [(1 + v/c)/(1
- v/c)]1/2 - 1 if the samples approach each other.
We can
solve for v/c ~ 3*10-13. v ~ 10-4 m/s.
(e)
The counting rate of a gamma-ray detector increases for both directions,
because the sample 57Fe absorbs less.
(f) A 14.4 keV
gamma emitted from 57Fe ray travels vertically upward in a
uniform gravitational field.
We have Δf/f = -gΔh/c2 from E2/E1
= 1 - g(h2 - h1)/c2. Δf/f = -2.45*10-15.
Such a shift can also be produced if the absorber moves away from the
source.
We would need Δf/f = [(1 - v/c)/(1 + v/c)]1/2 -1 =
-2.45*10-15, v/c = 2.45*10-15 away from source.
(g) The absorber has to move towards the source with v/c = 2.45*10-15
in order to increase, in its own frame, the frequency for optimum
absorption, because the frequency was decreased by the gravitational
redshift.
If the absorber is at rest we still have absorption, since
Δf/f|g << 3*10-13.