Decay involving only massive particles

Problem:

A slowly moving antiproton is captured by a deuteron at rest producing a neutron and a neutral pion.

p + D --> n + π⁰

The rest masses of the particles involved are m_pc² ≈ m_nc² ≈ m_Dc²/2 ≈ 939 MeV and m_π0c² = 135 MeV.  Find the total energy of the emitted π⁰.

Solution:

• Concepts:
  Relativistic collisions, energy and momentum conservation
• Reasoning:
  In relativistic collisions energy and momentum are always conserved. 
• Details of the calculation:
  We assume that the initial particles have no kinetic energy.
  Energy conservation:  E = 3m_pc² = E_n + E_π0.                      (1)
  Momentum conservation: p_n = p_π0.                                   (2)
  E_n² = p_n²c² + m_p²c⁴_,  E_π0² = p_n²c² + m_π0²c⁴,
  E_n² - E_π0² = (E_n + E_π0)(E_n - E_π0) = m_p²c⁴  - m_π0²c⁴.              (3)
  (E_n - E_π0) = (m_p²c⁴  - m_π0²c⁴)/(3m_pc²).                              (4) = (3)/(1)
  2E_π0 = 3m_pc² - (m_p²c⁴  - m_π0²c⁴)/(3m_pc²).                          (1) - (4)
  E_π0 = (8m_p²c⁴  + m_π0²c⁴)/(3m_pc²) = 1255 MeV.

Problem:

A K⁰ meson decays in flight into two pions,  K⁰ --> π⁺ + π^-.  Let the mass of each pion be m_π and the mass of the K⁰ be m_K > 2m_π.  
(a)  Find the speed of the K⁰ if the greatest possible energy of a π-meson from this decay is α times larger than the smallest possible energy. 
(b)  For what α will there be no π-meson flying into the backward hemisphere?

Solution:

• Concepts:
  Relativistic "collisions", energy and momentum conservation, Lorentz transformation
• Reasoning:
  The decay of a particle is a relativistic problem.  In relativistic "collisions" energy and momentum are always conserved.
• Details of the calculation:
  (a)  Let the K⁰ meson move in the positive x direction. The pion with the greatest possible energy in the laboratory is emitted into the +x direction and the pion with the smallest possible energy is emitted in the -x direction.
  In the rest frame of the K⁰ meson we have for the forward emitted pion,
  E/c = m_Kc/2, p_x = (m_K²c²/4 - m_π²c²)^½ = (m_Kc/2)(1 - 4m_π²/m_K²)^½.
  For the backward emitted pion we have
  E/c = m_Kc/2, p_x = -(m_K²c²/4 - m_π²c²)^½ = -(m_Kc/2)(1 - 4m_π²/m_K²)^½.
  A Lorentz transformation to the lab frame yields:
  Forward emitted pion: E_f = γ[(m_Kc/2) + β(m_Kc/2)(1 - 4m_π²/m_K²)^½]
  Backward emitted pion: E_b = γ [(m_Kc/2) - β(m_Kc/2)(1 - 4m_π²/m_K²)^½]
  E_f/E_b = α = [1 + β(1 - 4m_π²/m_K²)^½]/[1 - β(1 - 4 m_π²/m_K²)^½]
  β = v/c = (1 - 4m_π²/m_K²)^-½(α - 1)/(α + 1)
  
  (b)  We want p_x of the backward emitted pion to be positive in the lab frame
  p_x = γ [β(m_Kc/2) - (m_Kc/2)(1 - 4m_π²/m_K²)^½] = 0.
  β = (1 - 4m_π²/ m_K²)^½, α = (1 + β²)/(1 - β²) = m_K²/(2m_π²) - 1
  For α > m_K²/(2m_π²) - 1 there will there be no π-meson flying into the backward hemisphere?

Problem:

A Higgs boson (M = 178 GeV/c²) at rest decays into a pair of leptons (φ --> τ⁺τ^-).  The τ^- has a mass of m = 1.78 GeV/c².  What is the recoil β = v/c of the τ⁺?

Solution:

• Concepts:
  Relativistic "collisions", energy and momentum conservation
• Reasoning:
  The decay of a particle is a relativistic problem.  In relativistic "collisions" energy and momentum are always conserved.
• Details of the calculation:
  The tau leptons emerge from the decay in opposite directions with equal energy.
  2E_τ = Mc².  E_τ = (m²c⁴ + p_τ²c²)^½.
  p_τ = (M²/4 - m²)^½c,  E_τ = Mc²/2,   
  β = p_τc/ E_τ  = (1 - 4m²/M²)^½ = (1 - 4*10^-4)^½ = 0.9998... .

Problem:

A Φ particle (m_Φ = 1.020GeV/c²) has a momentum of 3GeV/c along the z-axis in the laboratory frame. 
It decays Φ --> K⁺K^- into two charged kaons (m_K⁺ = m_K^- = 0.494GeV/c² ).
(a)  Calculate the momentum P_K of each kaon in the laboratory frame if the decay axis coincides with the z-axis.
(b)  Calculate the momentum P_K of each kaon in the laboratory frame if the decay axis is perpendicular to the z-axis.

Solution:

• Concepts:
  Relativistic "collisions", energy and momentum conservation
• Reasoning:
  The decay of a particle is a relativistic problem.  In relativistic "collisions" energy and momentum are always conserved.  Often the physics is best visualized in the center of momentum frame.
• Details of the calculation:
  In the rest frame of the m_Φ, the 4-vector momentum of the Φ is (E/c,p) = (m_Φc, 0).
  Each component of the 4-vector is conserved.  After the decay we therefore have for each particle:
  E_k² = ¼m_Φ²c⁴ = m_k²c⁴ + p_k²c²,  p_k² = c²(¼m_Φ² - m_k²).
  E_k = 0.51 GeV,  p_k = 0.127 GeV/c.
  The laboratory frame moves with respect to the rest frame in the negative z-direction with speed v.
  E_Φ' = γE_Φ,  E_Φ'² = γ²E_Φ²,  m_Φ²c⁴ + p_Φ²c² = γ²E_Φ²,  γ² = [1.02² + 3²]/1.02² , γ  = 3.1.
  b = 0.947, v =  0.947c.
  We can now find the momentum of each kaon in the laboratory frame.
  
  
  
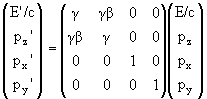
  (a)  Particle 1: E = E_k, p_z = p_k, p_x = p_y = 0.  p_z' = 1.89 GeV/c.
  Particle 2: E = E_k, p_z = -p_k, p_x = p_y = 0.  p_z' = 1.11 GeV/c.

  (b)  Particle 1:  E = E_k, p_z = 0, p_x = p_k, p_y = 0.  p_z' = 1.5 GeV/c, p_x' = 0.127 GeV/c.
  Particle 2:  E = E_k, p_z = 0, p_x = -p_k, p_y = 0.  p_z' = 1.5 GeV/c, p_x' = -0.127 GeV/c.
  For both particles: |p'| = (p_x'² +p_z'²)^½ = 1.505 GeV/c.

Problem:

A particle of mass M is at rest in the laboratory.  Suddenly it disintegrates into two particles, one of mass m and one of mass 2m.  Let M = 4m.  The final particles have momenta p and p', and energies E and E'.
(a)  What is the relationship between p and p'?
(b)  Find expressions for p, p', E, and E'.
(c)  Determine the speed of each final particle in the laboratory frame.
(d)  Determine the speed of m in the rest frame of 2m.

Solution:

• Concepts:
  Relativistic "collisions", energy and momentum conservation
• Reasoning:
  The decay of a particle is a relativistic problem.  In relativistic "collisions" energy and momentum are always conserved.
• Details of the calculation:
  (a)  Momentum conservation requires that p = -p'.
  (b)  Energy conservation:  Mc² = 4mc² = (m²c⁴ + p²c²)^½ + (4m²c⁴ + p²c²)^½.
  4mc² - (m²c⁴ + p²c²)^½ = (4m²c⁴ + p²c²)^½.  Solve for pc!
  pc = 1.281 mc².
  E = (m²c⁴ + 1.64 m²c⁴ )^½ = 1.625 mc².
  E' = (4m²c⁴ + 1.64 m²c⁴ )^½ = 2.375 mc².
  (c) p = γmv.  E = γmc².  v = pc²/E
  v/c = 1.281 mc²/1.625 mc² = 0.788.
  v'/c =  1.281 mc²/2.375 mc² = 0.539.
  Velocity addition formula:
  Let v'' be the speed of m in the rest frame of 2m.  v'' = (v + v')/(1 + vv'/c²) = 0.93c.

Problem:

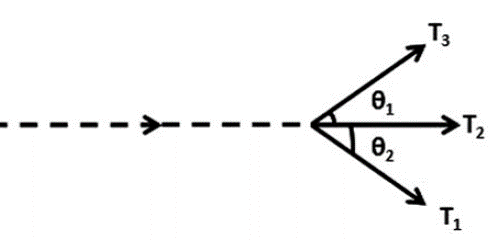
An unstable particle decays in its flight into three charged pions (mass 140 MeV/c²).  The tracks recorded are shown below, the event being coplanar.  The kinetic energies and the emission angles are T₁ = 190 MeV, T₂ = 321 MeV, T₃ = 58 MeV, θ₁ = 12.25^o, θ₂ = 22.4^o.  Estimate the mass of the primary particle.  In what direction was it moving?

Solution:

• Concepts:
  Energy and momentum conservation
• Reasoning:
  We find the momenta of three pions by using the formula p²c² = E² - m²c⁴.
• We use energy and momentum conservation to find the mass of the decaying particle.
• Details of the calculation:
  E₁ = T₁ + m_πc² = 330 MeV,  p₁c = 299 MeV
  E₂ = T₂ + m_πc² = 461 MeV,  p₂c = 439 MeV
  E₃ = T₃ + m_πc² = 198 MeV,  p₃c = 140 MeV
  Energy conservation:  E = E₁ + E₂ + E₃ = 989 MeVE is the total energy of the decaying particle.
  Let the positive x-direction be the direction of motion of pion 2.
  p_1xc = 299 MeV*cos(22.4^o),  p_1yc = -299 MeV*sin(22.4^o).
  p_2xc = 439 MeV,  p_2yc = 0.
  P_3xc = 140 MeV*cos(12.25^o),  p_3yc = 140 MeV*sin(12.25^o).
  p_xc = 852.25 MeV, p_yc = -84.23 MeV, are the momentum components of the decaying particle (times c).
  pc = 856.4 MeV is the momentum of the decaying particle.
  mc² = (989² - 856.4²)^½ = 494.7 MeV.
  The decaying particle's mass is 494.7 MeV/c².  It is a kaon.
  tanθ = p_y/p_x,  θ = -5.64 ^o.
  The decaying particle's momentum was 856.4 MeV/c and it pointed in a direction making an angle of -5.64 ^o with the positive x-direction.