In the year 2310 construction of the large space colony "Heavy Metal" is finally completed. The distance between the "East" and "West" edges of the colony is 400 km in the rest frame of the colony. To celebrate the end of construction, two flares are lighted at midnight during a New Year's celebration at the "East" and "West" edges. The light from the flares reaches an observer at the center of the colony at the same time. A fast spacecraft flying with a constant speed of v = 0.95 c "East" to "West". Let Event 1 be flare is lighted on "East" edge and Event 2 be flare is lighted on "West" edge. In the reference frame of the spacecraft, does Event 1 occur before, after, or at the same time as Event 2? Explain your reasoning!
Solution:
A space traveler, moving with velocity vi with respect to Earth synchronizes his clock with a friend on Earth at t' = t = 0. The earthman then observes both clocks and simultaneously reads the times t and t' (t directly and t' through a telescope). What does t read when t' reads 1 hour?
Solution:
For an observer on Earth, the star Sirius is 8.8 ly away. Assume Sirius is
stationary with respect to Earth. At t = 0, a spaceship moving with velocity v
= 0.95 c i towards Sirius passes Earth. Earth and the ship synchronize
clocks.
An observer on Earth tells the following story at a much later time:
At t = 0, just as the spaceship passed Earth, a flare erupted on Sirius. The
light from the flare reached Earth at t = 8.8 y. At t = 0.9 years a comet hit
Earth. At t = 9.26 years the spaceship passed Sirius and sent us a light
signal. The signal reached us at 18.06 years.
How does an observer on the ship tell the same story?
Solution:
| Event: |
coordinates in K (Earth): (x0,x1,x2,x3) = (ct,x,y,z) |
coordinates in K' (ship): (x'0,x'1,x'2,x'3) = (ct',x',y', z') |
| #1: Ship passes Earth | (0, 0, 0, 0) | (0, 0, 0, 0) |
| #2: Flare erupts on Sirius | (0, l2, 0, 0) | (ct2', l2', 0, 0) |
| #3: Comet his Earth | (ct3, 0, 0, 0) | (ct3', l3', 0, 0) |
| #4: Ship passes Sirius | (ct4, l4, 0, 0) | (ct3', 0, 0, 0) |
| #5: Signal reaches Earth | (ct5, 0, 0, 0) | (ct5', l5', 0, 0) |
Event 2:
l2 = 8.8 ly, γ = (1 - β2)-½ = 3.2,
ct2' = γct2 - γβx2 = (-3.2)(0.95)(8.8 y),
t2' = - 26.8 years.
l2' = γl2' = 28.2 ly.
Event 3:
t3 = 0.9 y.
ct3' = γct3 - γβx3 = γct3, t3'
= (3.2)(0.9 y) = 2.9 years.
l3' = -γβct3 = -(3.2)(0.95)(0.9)ly = -2.74 ly. (Note:
c = 1ly/y)
Event 4:
t4 = 9.26 y, l4 = 8.8 ly, ct4' = γct4
- γβx4, t4' = 3.2[9.26 y - (0.95)(8.8 y)] = 2.9 y.
The distance between the Earth and the ship as measured from the ship is d =
(8.8 ly)/γ = 2.7 ly.
Event 5:
t5 = 18.06 y. t5' = γt5 = (3.2)(18.06 y) =
57.8 y.
l5' = -γβct5 = -(3.2)(0.95)(18.06 ly) = -54.9 ly.
The story told by an observer on the ship:
A flare erupted on Sirius when the ship was 28.2 ly from Sirius, 26.8 years
before we reached Earth. At t = 0 we passed Earth.
A comet hit earth at 2.88 years after we had passed Earth, when it lay 2.74
ly behind us. At the same time we passed Sirius and sent a light signal
back to Earth. That signal reached Earth at t = 57.8 y, when it lay 54.9 ly
behind us.
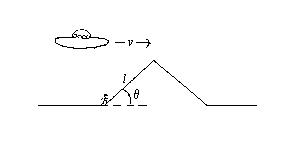
A pyramid in the Egyptian desert (see the figure) has sides of length l
inclined at an angle θ according to Egyptian references. An archeologist at the
base of the pyramid begins moving up the side of the pyramid and reaches the top
of the pyramid in time T according to observers on the ground. A spaceship,
moving in the positive x-direction, is approaching the pyramid at a relativistic
velocity v.
(a) According to observers in the spaceship, how far did the archeologist move
and how long did it take him to reach to top of the pyramid?
(b) Give two calculations of the invariant space-time interval ∆s2
for the archaeologist's ascent: one, using the inertial frame of the spaceship,
and the other, using the inertial frame of the ground.
For part (c), assume that the archeologist moved up the pyramid at a constant
velocity v0 = l/T. Do not neglect v0 compared to c.
(c) Calculate the proper time required for the archeologist's ascent.

Solution:
| x0' | ||
| x1' | ||
| x2' | ||
| x3' |
=
| γ | -γβ | 0 | 0 | ||
| -γβ | γ | 0 | 0 | ||
| 0 | 0 | 1 | 0 | ||
| 0 | 0 | 0 | 1 |
| x0 | ||
| x1 | ||
| x2 | ||
| x3 |
.
| x0 | ||
| x1 | ||
| x2 | ||
| x3 |
=
| γ | γβ | 0 | 0 | ||
| γβ | γ | 0 | 0 | ||
| 0 | 0 | 1 | 0 | ||
| 0 | 0 | 0 | 1 |
| x0' | ||
| x1' | ||
| x2' | ||
| x3' |
.
Here (x0,x1,x2,x3) = (ct,x,y,z),
β = v/c, γ = (1 - β2)-½.
Assume that at t = t' = 0 the origins of the two coordinate systems coincide
at r = r' = 0.
In K the archeologist's position 4-vector when he reaches the top is (cT,
lcosθ, lsinθ, 0).
In K' it is (cT', x', y', 0), with
cT' = γcT - γβlcosθ, x' = -γβcT + γlcosθ, y' = lsinθ.
T' = γ(T - (v/c2)lcosθ) is the time it takes the archeologist to
get to the top in K'.
He moves a distance d' = [γ2(lcosθ -vT)2 + (lsinθ)2]½.
(b) In K: ∆s2 = c2∆t2 - |∆r|2
= c2T2 - (lcosθ)2 - (lsinθ)2 = c2T2
- l2.
In K': ∆s2 = c2∆t'2 - |∆r'|2
= c2γ2(T - (v/c2)lcosθ)2 - γ2(lcosθ
- vT)2 - (lsinθ)2
= γ2[c2T2 - 2βcTlcosθ + β2(lcosθ)2
- (lcosθ)2- (vT)2 + 2lvcosθT] - (lsinθ)2
= γ2[c2T2(1 - v2/c2)
- (lcosθ)2(1 - β2)] - (lsinθ)2 = c2T2
- l2.
(c) The proper time is calculated in the archeologist's rest frame. He
moves with constant velocity v0 = l/T with respect to an observer
at rest at the foot of the pyramid.
∆τ = ∆t/γarch = T(1 - v02/c2)½
= (T2 - l2/c2)½ = ∆s/c.
Consider three reference frames. A meter stick is at rest in frame K2.
It is positioned on the x-axis, from x = 0 to x = 1m. Frame K2 moves
with velocity v = v2j in the positive y-direction with
respect to frame K1. Frame K3 moves with velocity
v
= v3i in the positive x-direction with respect to frame K1.
(a) Find the velocity of the stick in K3.
(b) Find the length of the stick in K3.
(c) Find the angle θ the stick makes with the x-axis in K3.
Solution:
u'|| =
(u|| - v)/(1 - v∙u/c2)
u'⊥
= u⊥/(γ(1 - v∙u/c2))
where parallel and perpendicular refer to the direction of the relative velocity v.
Here v = v3i, u|| = 0, u⊥
= v2j.
Therefore ux' = -v3, uy' = v2/γ3
= (1 - v32/c2)½v2.
We can also proceed by transforming the coordinates of events. Let us
look at the positions of the left and the right end of the stick at t = 0
and at t = t1 in K1 and K3.
To transform the coordinates of an event from K1 to K3
we use the matrix equation below.
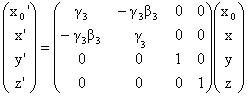
| Event: | coordinates in K1 | coordinates in K3 |
| (1) left edge at t = 0 | (0, 0, 0, 0) | (0, 0, 0, 0) |
| (2) right edge at t = 0 | (0, L, 0, 0) | (-γ3β3L, γ3L, 0, 0) |
| (3) left edge at t = t | (ct, 0, v2t, 0) | (γ3ct, -γ3β3ct, v2t, 0) |
| (4) right edge at t = t | (ct, L, v2t, 0) | (γ3ct-γ3β3L, -γ3β3ct+γ3L, v2t, 0) |
From events 1 and 3 we find ux' = Δx'/Δt' = -γ3β3ct/γ3t
= -β3c = -v3.
From events 1 and 3 we find uy' = Δy'/Δt' = v2t/γ3t
= v2/γ3.
(b) In K3 at t' = 0 the left edge of the stick is at x' = 0, y'
= 0.
At t' = -γ3β3L/c the right edge of the stick is at x'
= γ3L, y' = 0.
The stick travels with velocity u' = -v3i + (v2/γ3)j.
Therefore at t' = 0 the right edge of the stick is at
x' = γ3L - v3γ3β3L/c, y' = (v2/γ3)γ3β3L/c,
or x' = γ3L(1 - β32) = L/γ3, y'
= β2β3L.
The length of the stick in K3 is (x'2 + y'2)½
= L(1 - β32 + (β2β3)2)½.
(c) tanθ' = y'/x' = β2β3γ3.
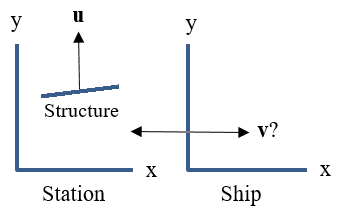
A spaceship travels with velocity v = vi with respect to a
space station. In the frame of the space station a linear structure of
length L = 10 km moves with velocity u = (c/2)j in the positive y
direction. The structure lies in the xy-plane and makes an angle θ = 7.2o
with the x axis? When viewed from the spaceship, the structure is aligned
with the x-axis.
(a) What is the velocity v of the spaceship
(magnitude and direction)?
(b) What is the length of the structure in the
frame of the spaceship'?
Solution:
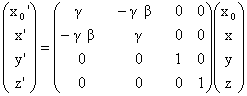
| Event: | coordinates in K | coordinates in K' |
| (1) left edge at t = 0 | (0, 0, 0, 0) | (0, 0, 0, 0) |
| (2) right edge at t = 0 | (0, Lcosθ, Lsinθ, 0) | (-γβLcosθ, γLcosθ, Lsinθ, 0) |
| (3) left edge at t = t | (ct, 0, ut, 0) | (γct, -γβct, ut, 0) |
| (4) right edge at t = t | (ct, Lcosθ , Lsinθ + ut, 0) | (γct - γβLcosθ, -γβct + γLcosθ, Lsinθ + ut, 0) |
From events 1 and 3 we find vx' = ∆x'/∆t' = -γβct/γt = -βc
= -v.
From events 1 and 3 we find vy' = ∆y'/∆t' = ut/γt = u/γ.
In K' at t' = 0 the left edge of the stick is at x' = 0, y' = 0.
At t' =
-γβLcosθ/c the right edge of the stick is at x' = γLcosθ, y' = Lsinθ.
The
stick travels with velocity v' = -v i + (u/γ) j.
Therefore
at t' = 0 the right edge of the stick is at x' = γLcosθ - vγβLcosθ/c,
y' = Lsinθ + (u/γ)γβLcosθ/c,
or x' = γLcosθ(1 - β2), y' =
L(sinθ + uvcosθ/c2).
For y' = 0 at t' = 0 we need sinθ + uvcosθ/c2
= 0, v = -tanθ c2/u = -2 tan(7.2o)c = -0.25 c.
The ship is traveling in the negative x direction with velocity
v =
-0.25c i with respect to the station.
(b) At t' = 0 the
left edge of the stick is at x' = 0, y' = 0, the right edge of the stick is
at
x' = γLcosθ(1 - β2), y' = 0, the length of the stick is L'
= x' = γLcosθ(1 - β2) = 0.96L = 9.6 km.
A spaceship has length 100 m in its own reference frame. It travels at v =
0.95 c with respect to earth. Suppose that the tail of the spaceship emits a
flash of light.
(a) In the reference frame of the spaceship, how long does it take the light to
reach the nose?
(b) In the frame of the earth, how long does it take the light to reach the
nose?
Solution:
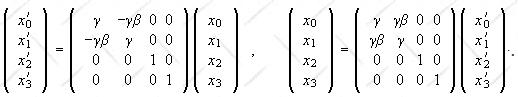
| in K | in K' | |||
| coordinates: | x | ct | x' | ct' |
| Event 1: tail emits pulse | 0 | 0 | 0 | 0 |
| Event 2: nose receives pulse | 100 | 100 | -γβ100 + γ100 | γ100 - γβ100 |
t' = (γ100 - γβ100)/c = (100 m)(3.2 + 3.04)/(3*108
m/s) = 2.08 μs.
or:
In the frame of the earth it takes the light 100 m(γ - γβ)/(3*108
m/s) = (100 m)(3.2 + 3.04)/(3*108 m/s) = 2.08 μs to reach the nose.
(a) Observer A is stationary in a laboratory on Earth's surface and
observer B is in a laboratory moving at high velocity parallel to Earth's
surface (neglect the curvature of the earth in the subsequent considerations)
and parallel to the x axis. Assume that the observers each witness
two separate lightning strikes on the surface of the earth lying along the x
axis.
(i) Describe concisely a practical scheme whereby observer A can
determine whether the two lighting strikes occurred simultaneously in her
reference frame.
(ii) Show that if observer A concludes from her
observations that the strikes were simultaneous, observer B generally must
conclude from his observations of the same events that the strikes are not
simultaneous, thus demonstrating that simultaneity is a relative and not
absolute concept.
(b) Einstein was strongly inspired by Maxwell's
theory of electromagnetism and viewed Galilean invariance for transformations
between reference frames as being seriously flawed because it was inconsistent
with Maxwell's theory. The special theory of relativity removed this
inconsistency. Explain the meaning of the preceding two statements.
Solution:
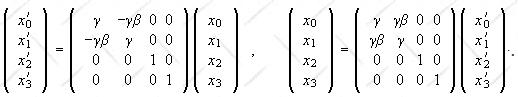
In the frame of observer B we have from the
Lorentz transformation that the coordinates for event 1 are (ct1', x1', y1',
z1') = (-γβd1, γd1, 0, 0), and the
coordinates for event 2 are (ct2', x2', y2',
z21') = (-γβd2, γd2, 0, 0).
Since
d1 is not equal to d2, we have t1' not
equal to t2'. The two lightning strikes do not occur
simultaneously in the frame of observer B.
(b) Maxwell's equations
predict that electromagnetic fields satisfy a wave equation in free space.
The equations do not contain any reference to a medium, and the propagation
speed of any electromagnetic wave through the vacuum is c, regardless of the
relative motion of the source and the observer. The Galilean
transformation predicts that the speed of electromagnetic waves depends on
the relative motion of the source and the observer.
The special theory of
relativity removes this inconsistency.
The postulates of special relativity are:
I. The laws of nature are
the same in all inertial reference frames.
II. In vacuum, light
propagates with respect to any inertial frame and in all directions with the
universal speed c. This speed is a constant of nature.
The second postulate of the special theory of relativity, however, goes beyond just Maxwell's equations. Important parts of physics, such as the physics of elementary particles, cannot possibly be explained in terms of electrodynamics.
(a) Show that if two events are separated in space and time so that no
signal leaving one event can reach the other, then there is an observer for whom
the two events are simultaneous.
(b) Show that the converse is also
true: if a signal can get from one event to the other, then no observer will
find them simultaneous.
(c) Show if a signal can get from one event to
the other, then there is an observer for whom the two events have the same space
coordinates, i.e. for whom the two events "happen at the same place".
Solution:
(b) Let ct1,
r1 and ct2,
r2 be the
coordinates of events 1 and 2 in K and let
|r2 -
r1|
= |∆r| < c(t2 - t1) = c∆t. Then it is possible
for a signal leaving event 1 to reach event 2 in K.
Choose a reference
frame K' that moves with velocity β with respect to K where
β
points into the direction of ∆r. Then c∆t' = γ(c∆t - β|∆r|)
= γ|∆r| (c∆t/|∆r| - β).
Since |∆r|
< c∆t, c∆t/|∆r| >1 and we cannot choose β < 1 such that c∆t/|∆r|
- β = 0.
Therefore c∆t' > 0 in every frame. No observer will
find the events simultaneous.
(c) Let ct1,
r1
and ct2, r2 be the coordinates of events 1 and
2 in K and let
|r2 -
r1| = |∆r|
< c(t2 - t1) = c∆t. Then it is possible for a signal
leaving event 1 to reach event 2 in K.
Choose a reference frame K' that
moves with velocity β with respect to K where
β points into
the direction of ∆r. Then
r'⊥ =
r⊥
= 0 and ∆r' = γ(∆r -
βc∆t) = γ c∆t (∆r/(c∆t)
- β).
Since |∆r| < c∆t, (|∆r|/(c∆t)
< 1 and we can choose β < 1 such that (∆r/(c∆t) -
β) = 0.
Then r' = 0, the two events have the same space coordinates.
Two events "occur" at the same place in the laboratory frame of reference and
are separated in time by 3 seconds.
(a) What is the spatial distance between these events in a rocket frame moving
with respect to the laboratory frame, in which the events are separated in time
by 5 seconds?
(b) What is the relative speed of the moving frame and the laboratory frame?
Solution:
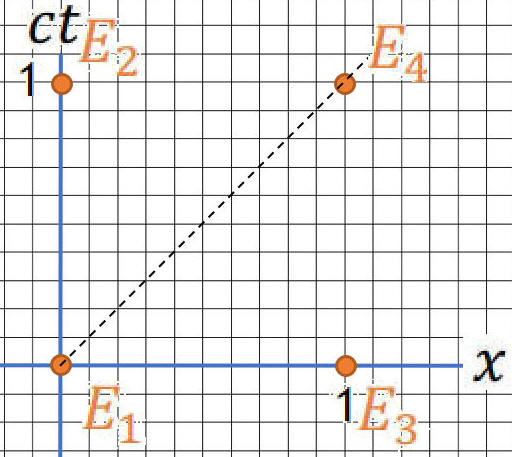
Consider 4 events in an inertial reference frame S with space time coordinates (ct, x).
E1 = (0, 0), E2, = (1,0), E3 = (0,
1), E4 = (1,1), (arbitrary units).
(a) Draw a space-time diagram for S, showing the 4 events. Which
pairs of events have space-like, time-like, or light-like separation? Are
there simultaneous events?
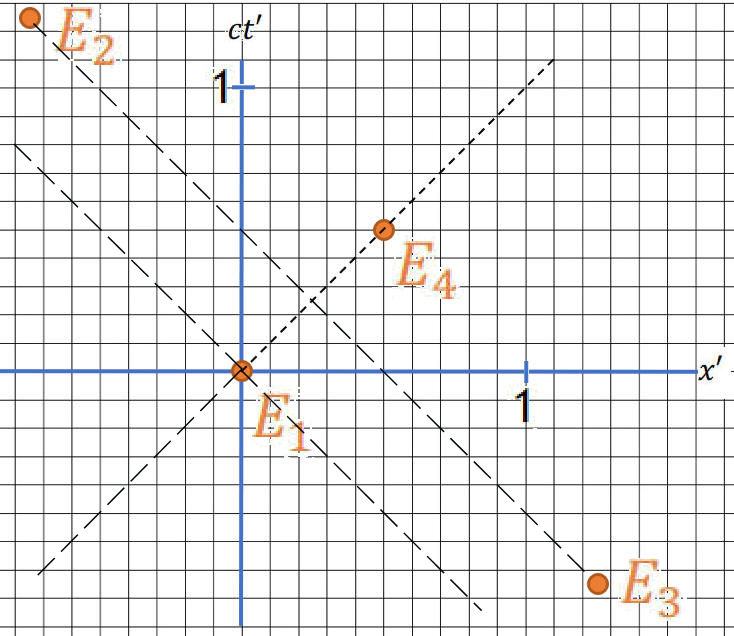
(b) Use the Lorentz transformation to plot these events in a space-time diagram
for an inertial reference frame S' with axes (ct', x'). S' is moving with velocity v = 0.6c i with respect to x.
Which events are simultaneous? Which pairs of events have space-like,
time-like, or light-like separation? Are there simultaneous events?
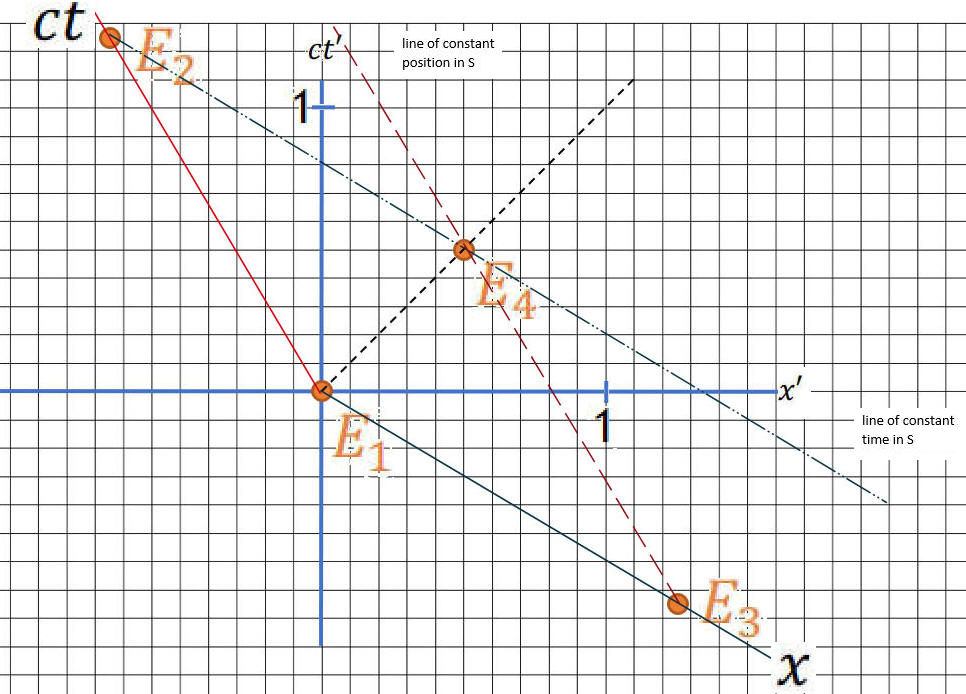
(c) The space-time diagram of S can be overlaid on the space-time diagram of S'
as a tilted co-ordinate system.
Draw the ct axis an the x axis of S in the space-time diagram of S'.
Comment on the direction of lines of constant position and lines of constant
time in reference frame S in the space-time diagram for reference frame S'.
Solution: