The proper length

Problem:

A car of rest length 5 m passes through a garage of rest length 4 m.  Due to Lorentz contraction, the car is only 3 m long in the garage's rest frame.  Find the length of the garage in the car's rest frame.

Solution:

• Concepts:
  Lorentz contraction
• Reasoning:
  To an observer in motion relative to an object, the dimensions of the object are contracted by a factor of 1/γ in the direction of motion.
• Details of the calculation:
  L' = L₀/γ,  γ = (1 - v²/c²)^-½.
  From the data given for the car we calculate γ = 5/3.
  Length of garage in it's the car's rest frame = (4 m)/γ = 2.4 m.

Problem:

The radius of the galaxy is 3*10²⁰m, measured in its own rest frame.
(a)  If the time it takes a spaceship to cross the entire galaxy is 300 years measured in the spaceship's rest frame, what is the relative speed of spaceship and galaxy?
(b)  How much time elapses on Earth during this trip?

Solution:

• Concepts:
  Relativistic kinematics, the proper time interval, Lorentz contraction
• Reasoning:
  We are given the proper time interval between two events and the space coordinate of these two events in another frame.
• Details of the calculation:
  (a)  τ = 300 years.  This is the time interval between when opposite edges of the galaxy pass the spaceship.
  L = L₀/γ is the diameter of the galaxy in the frame of the spaceship.
  L₀ = 6*10²⁰ m = 6.34*10⁴ ly.
  v = L/τ =  L₀/(γτ).
  v² = (1 - v²/c²)L₀²/τ²,  v²/c² = L₀²/(c²τ² + L₀²).
  v/c = 0.99998 c.
  (b)  t = L₀/v = 6.34*10⁴ years.

Problem:

A space ship has a proper length of 100 m.  It travels close to the Earth's surface with a constant speed of 0.8 c.  Earth observers decide to measure the length of the ship by erecting two towers that coincide with the ends of the ship simultaneously (in the Earth's frame) as it passes by.
(a)  How far apart do the observers on Earth build the towers?
(b)  How long do the observers on Earth say it takes for the nose of the ship to travel from tower A to tower B?
(c)  How long, according to the measurements in the spaceship frame, does it take for the nose of the ship to travel from tower A to tower B?
(d)  As measured by passengers in the spaceship, how far apart are the two towers?
(e)  In the spaceship frame, how long does it take a beam of light to travel from the front to the rear of the spaceship?
(f)  How much time, according to the observers on Earth, is required for a beam of light to travel from the front to the rear of the moving spaceship?
(Give numerical answers!)

 Solution:

• Concepts:
  Relativistic kinematics
• Reasoning:
  We are asked to compute various space and time intervals in different inertial frames.
• Details of the calculation:
  (a)  Length contraction:  L = L₀/γ, γ = (1 - v²/c²)^-½ = 1/0.6 = 1.667.
  L = 60 m is the distance between the towers.
  (b)  t = L/v = (60 m)/(2.4*10⁸ m/s) = 2.5*10^-7 s.
  (c)  τ = t/γ = 1.5*10^-7 s.  In the spaceships frame the two events have the same space coordinates, τ is the proper time.
  (d)  d_s = vτ  = (2.4*10⁸ m/s)(1.5*10^-7 s) = 36 m.
  (e)  t_s = (100 m)/(3*10⁸ m/s) = 3.33*10^-7 s.
  (f)  ct_e = 60 m - vt_e,  t_e = (60 m)/(1.8*3*10⁸ m/s) = 1.11*10^-7 s.

Problem:

Assuming that the rest radius of earth is 6,400 km and its orbital speed about the sun is 30 km/s, how much does earth's diameter appear to be shortened along its direction of motion to an observer on the sun?

Solution:

• Concepts:
  Lorentz contraction
• Reasoning:
  To an observer in motion relative to an object, the dimensions of the object are contracted by a factor of 1/γ in the direction of motion.
• Details of the calculation:
  β = v/c = (30 km/s)/(3*10⁵ km/s) = 10⁻⁴
  1/γ = (1 − β²)^½ ~ (1 - ½β²)
  ΔL = L₀ − L = L₀ − L₀/γ = L₀ − L₀(1 - ½β²) = ½ L₀β² = ½ * 6.4*10⁶ m * 10^-8 = 3.2 cm
  The earth diameter appears to be shortened by 3.2 cm along its direction of motion.

Problem:

A space ship has a proper length of 100 m.  It travels close to the Earth's surface with a constant speed of 0.8 c.  Earth observers decide to measure the length of the ship by erecting two towers that coincide with the ends of the ship simultaneously (in the Earth's frame) as it passes by.
(a)  How far apart do the observers on Earth build the towers?
(b)  How long do the observers on Earth say it takes for the nose of the ship to travel from tower A to tower B?
(c)  How long, according to the measurements in the spaceship frame, does it take for the nose of the ship to travel from tower A to tower B?
(d)  As measured by passengers in the spaceship, how far apart are the two towers?
(e)  In the spaceship frame, how long does it take a beam of light to travel from the front to the rear of the spaceship?
(f)  How much time, according to the observers on Earth, is required for a beam of light to travel from the front to the rear of the moving spaceship?
(Give numerical answers!)

Solution:

• Concepts:
  Relativistic kinematics
• Reasoning:
  We are asked to compute various space and time intervals in different inertial frames.
• Details of the calculation:
  (a)  Length contraction:  L = L₀/γ, γ = (1 - v²/c²)^-½ = 1/0.6 = 1.667.
  L = 60 m is the distance between the towers.
  (b)  t = L/v = (60 m)/(2.4*10⁸ m/s) = 2.5*10^-7 s.
  (c)  τ = t/γ = 1.5*10^-7 s.  In the spaceships frame the two events have the same space coordinates, τ is the proper time.
  (d)  d_s = vt = (2.4*10⁸ m/s)( 1.5*10^-7 s) = 36 m.
  (e)  t_s = (100 m)/(3*10⁸ m/s) = 3.33*10^-7 s.
  (f)  vt_e + ct_e = 60 m,  t_e = (60 m)/(1.8*3*10⁸ m/s) = 1.11*10^-7 s.

Problem:

A rod of length L₀ is inclined at angle θ from the x-axis in its rest frame.  Find the inclination angle of the rod as measured by an observer moving with relativistic speed "v" in the x-direction.

Solution:

• Concepts:
  Relativistic Kinematics, Lorentz contraction
• Reasoning:
  To an observer in motion relative to an object, the dimensions of the object are contracted by a factor of 1/γ in the direction of motion.
• Details of the calculation:
  In the rods rest frame: L_x = L₀cosθ, L_y = L₀sinθ.
  In the observers rest frame L_x' = L_x/γ, L_y' = L_y.  Here γ = (1 - v²/c²)^-½.
  tanθ' = L_y'/L_x' = γ tanθ.

Problem:

A rectangular plate of dimensions a × b moves at relativistic velocity V = Vi as shown in the figure.  In the rest frame of the rectangle, side a makes an angle θ with respect to the x axis.

(a)  Sketch the shape of the plate as measured by an observer in the laboratory frame.  Write down expressions for the lengths of all sides and the values of all interior angles in terms of β = V/c, γ = (1 - β²)^-½, and θ .
(b)  Evaluate your expressions for the case θ = π/4 and V = (2/3)^½c.

Solution:

• Concepts:
  Lorentz contraction
• Reasoning:
  An observer in the lab frame will measure lengths parallel to the x-axis contacted by a factor of γ^-1.
  γ = (1 - β²)^-½, β = V/c.  Lengths perpendicular to the x-axis are not contracted.
• Details of the calculation:
  
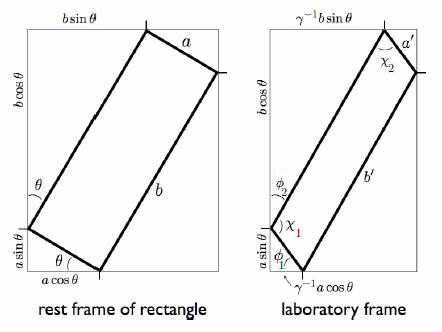
  From trigonometry:
  tanΦ₁ = γtanθ,  tanΦ₂ = γ^-1tanθ,
  a' = a(γ^-2cos²θ + sin²θ)^½ = a(1 - β²cos²θ)^½,
  b' = b(γ^-2sin²θ + cos²θ)^½ = a(1 - β²sin²θ)^½,
  Χ₁ = ½π + tan^-1(γtanθ) - tan^-1(γ^-1tanθ),
  Χ₂ = ½π - tan^-1(γtanθ) - tan^-1(γ^-1tanθ).
  
  (b)  For the case θ = π/4 and V = (2/3)^½c we have γ = (3)^½.
  Φ₁ = π/3, Φ₂ = π/6,  Χ₁ = 2π/3, Χ₂ = π/3.
  This yields a' = (2/3)^½a,  b' = (2/3)^½ b.

Problem:

A stick of length l is fixed at an inclination of angle θ from the x₁-axis in its own rest frame K.  Consider an observer in a frame K′ moving along the x₁-axis with speed v.  What does this observer measure for
(a)  the length of the stick and
(b)  the angle of the stick with respect to the x₁'-axis?

Solution:

• Concepts:
  Relativistic kinematics
• Reasoning:
  An observer in the frame K' will measure the projection of the length parallel to the x-axis contacted by a factor of γ^-1.
• Details of the calculation:
  (a)  In reference frame K  l_x = lcosθ,  l_y = lsinθ. 
  In reference frame K'  l'_x = l_x/γ = lcosθ/γ,  l'_y = l_y = lsinθ. 
  l' = (l'_x² + l'_y²)^½ = l(cos²θ/γ² + sin²θ)^½ = l(1 - cos²θ*v²/c²)^½.
  (b)  tanθ' = l_y'/l_x' = γtanθ.