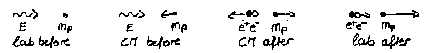Collisions including massless partners

Problem:

A photon of energy E (massless) hits a proton of mass M_p at rest.  After the collision the photon is converted into an e⁺e^- pair.  Assuming that the electron and positron each have rest mass m_e, what is the largest possible value of the recoil momentum of the proton?

Solution:

• Concepts:
  Relativistic collisions, energy and momentum conservation, frame transformations
• Reasoning:
  In relativistic collisions between free particles energy and momentum are always conserved.  Often the physics is best visualized in the center of momentum frame.
• Details of the calculation:
  The proton will have the largest possible value of recoil momentum, if in the CM frame the electron and the positron move as a unit with minimum internal energy (positronium) in the opposite direction.
  
  Neglect the binding energy of the positronium.  Let m₁ = m_e⁺ + m_e^- , m₂ = M_p.
  In the laboratory frame we have:
  energy conservation:  E + m₂c² = (m₁²c⁴ + p₁²c²)^½ + (m₂²c⁴ + p₂²c²)^½,
  momentum conservation:  (E/c)i = p₁i + p₂i.
  Let c = 1.  Then E + m₂ = (m₁² + p₁²)^½ + (m₂² + p₂²)^½,  E = p₁ + p₂. 
  We need to eliminate p₁ and solve for p₂ in terms of E, m₁, and m₂.
  E² + m₂² + 2Em₂ = m₁² + p₁² + m₂² + p₂² + 2(m₁² + p₁²)^½ (m₂² + p₂²)^½.
  E² = p₁² + p₂² + 2p₁p₂.
  (2p₁p₂ + 2Em₂ - m₁²)² = 4(m₁² + p₁²)(m₂² + p₂²).
  Write out all the terms, and substitute p₁ = E - p₂.  Obtain a quadratic equation for p₂.
  p₂² + Ap₂ + B = 0,  p₂ = -(A/2) ± [(A/2)² - B]^½.  With m₁ << m₂ we have
  A = E(m₁² - 2m₂² - 2Em₂)/(m₂² + 2Em₂) ≈ -E(2m₂ + 2E)/(m₂ + 2E) ,
  B = m₁²(m₂² + Em₂ - m₁²/4)/(m₂² + 2Em₂) ≈ m₁²(m₂ + E)/(m₂ + 2E)
  p_2max = -(A/2) + [(A/2)² - B]^½.

Problem:

Assume a photon with energy hν incident along the y-direction scatters off an electron with momentum p₀ along the x-direction.  After the scattering the photon travels in the x-direction.

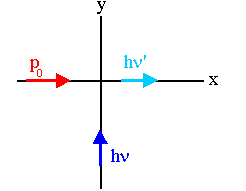
(a)  Find an expression for the energy of the scattered photon hν' in terms of hν and p₀.
(b)  What is the energy of the scattered photon if the energy of the incident photon is 5 eV and the kinetic energy of the incident electron is 100 eV?
(c)  What is the energy of the scattered photon if the energy of the incident photon is 5 eV and the energy of the incident electron is 1 GeV?

Solution:

• Concepts:
  Energy and momentum conservation in relativistic collisions
• Reasoning:
  In relativistic collisions between free particles energy and momentum are always conserved. 
• Details of the calculation:
  (a)
   

  	before:	after:
  electron energy:	E0 = (m2c4 + p02c2)½	E = (m2c4 + p2c2)½
  electron momentum:	p0 i	pcosθ i + psinθ j
  photon energy:	hν	hν'
  photon momentum:	(hν/c) j	(hν'/c) i

  conservation of:

  px	p0 = pcosθ + hν'/c	(1)
  py	hν/c = psinθ	(2)
  E	E0 + hν = E + hν'	(3)

  squaring (1):  (p₀ - hν'/c)²  = p²cos²θ

  squaring (2):  (hν/c)² = p²sin²θ

  adding:  p² = p₀² + (hν'/c)² - 2p₀ hν'/c + (hν/c)²  (4)

  squaring (3):  [E₀ + h(ν - ν')]²  = E² 
  h²(ν - ν')² + E₀²  + 2E₀h(ν - ν')  = m²c⁴ + p²c²
  = m²c⁴ + p₀²c² + (hν')² - 2p₀chν' + (hν)² (from 4)
  
  -h²νν' + E₀ hν - E₀ hν' + p₀chν' = 0
  hν' = E₀hν/(hν + E₀ - p₀c)

  
  (b)  Let hν = 5 eV, E₀ = T + mc² = 100 eV + mc².
  p₀²c² = E₀² - m²c⁴ = m²c⁴(1 - 100 eV/mc²)² - m²c⁴ ≈ 2mc² 100 eV.
  hν' ≈ 5 eV mc²/(mc² + 5 eV - (mc² 200 eV)^½)
  ≈ 5 eV mc²/{(mc²)^½ [(mc²)^½-(200 eV)^½]} ≈ 5 eV.
  For a slow electron the photon energy does not increase appreciably.
  (c)  Let hν = 5 eV, E₀ = T + mc² = 1 GeV + mc² ≈ 1 GeV.
  p₀²c² = E₀² - m²c⁴ ≈ (1 GeV)².
  hν' ≈ 5 eV 1 GeV/(5 eV + 1 GeV -1 GeV) ≈ 1 GeV.
  The photon energy increases appreciably for a relativistic electron.

  Link:
  An interesting experiment that uses the high-energy photons created that way:
  "Turning Light into Matter"

Problem:

(a)  Find the photon threshold energy in MeV for the photoproduction process

γ + p --> p + π⁰

(m_π0 = 135 MeV/c², m_p = 938 MeV/c²).

(b) Now consider the following problem.  The isotropic CMBR (Cosmic Microwave Background Radiation) of photons in space has a temperature of T = 2.726 K.  The most probable photon frequency (distributed according to Plank's radiation law) is
f = c/λ = 1.6*10¹¹ Hz, the corresponding photon energy is E_g = hf ~ 658 μeV.
Calculate the energy in MeV of a cosmic-ray proton that by interacting with a CMBR photon will produce a pion (π⁰) like in part (a).    

(c)  Calculate the mean free path of the proton in space for this process if the density of CMBR photons is 411 cm^-3 and the cross section is 0.5 mbarn (1 barn = 10^-24 cm²).

Solution:

• Concepts:
  Relativistic collisions, energy and momentum conservation, frame transformations
• Reasoning:
  In relativistic collisions between free particles energy and momentum are always conserved.  Often the physics is best visualized in the center of momentum frame.
• Details of the calculation:
  (a)  The photon has minimum energy when the reaction products are at rest in the CM frame.  In the lab frame the proton and pion move together as one particle with mass
  M = m_π0 + m_p.
  In the CM frame after the collision we have for the "length"² of the momentum 4-vector
  P₀² - P² = P₀²  = (∑p₀)² = (Mc)².
  The "length"² of the total momentum 4-vector is (Mc)² before and after the collision in the lab frame.
  Before the collision we have
  P₀² - P² = (hf/c + m_pc)² - (hf/c)² = m_p²c² + 2hfm_p = (Mc)².
  hf = m_π0(m_π0 + 2m_p)c²/(2m_p)  = 144.7 MeV is the minimum photon energy.

  (b)  In the rest frame of the proton, the photon energy must be greater than 144.7 MeV.
  How fast does the proton have to move for the energy of the CMBR photon to be Doppler shifted up to 144.7 MeV?
  Doppler shift:  f'/f = 658 μeV/144.7 MeV = [(1-v/c)/(1+ v/c)]^½.
  f'/f = 4.547*10^-12.  v/c = (1 - (f'/f)²)/(1 - (f'/f)²) = (1 - α)/(1 + α) with α = (f'/f)².
  1 - v²/c² = [1 + α)² - (1 - α)²]/(1 + α)² = 4α/(1 + α)² = 8.271*10^-23.
  γ = 1.1*10¹¹.
  γm_pc² ~ 1*10¹⁴ MeV is the energy of a cosmic-ray proton that by interacting with CMBR photon can produce a pion π⁰.
  (c)  Mean free path: λ = (σn)^-1.
  σ = cross section, n = density of targets.
  λ = (411 cm^-3 * 0.5*10^-27 cm²)^-1 = 4.87*10²² m ~ 5.14*10⁶ ly.

Problem:

Assume a γ-ray collides with a particle at rest.
(a) What is the threshold energy for the photon (expressed in terms of the electron mass) for the process γ + Pb --> e⁺ + e^- + Pb?
(c) What is the threshold energy for the photon (expressed in terms of the electron mass) for the process γ + e^- --> e⁺ + e^- + e^- where e^- is a free electron?
(c) Why are the threshold energies in Parts (a) and (b) different?

Solution:

• Concepts:
  Relativistic collisions, energy and momentum conservation, frame transformations
• Reasoning:
  In relativistic collisions between free particles energy and momentum are always conserved.  Often the physics is best visualized in the center of momentum frame.
  The photon has minimum energy when the reaction products are at rest in the CM frame. 
• Details of the calculation:
  (a)  In the CM frame after the collision we have for the "length"² of the momentum
  4-vector P₀² - P² = P₀²  = (∑p₀)² = (Mc)², where Mc² = ∑m_ic² = (m_Pb + 2m_e)c².
  The "length"² of the total momentum 4-vector is (Mc)² before and after the collision in the lab frame.
  Before the collision we have
  P₀² - P² = (hf/c + m_Pbc)² - (hf/c)² = m_Pb²c² + 2hfm_Pb = (Mc)².
  hf = 4m_e(m_e + m_Pb)c²/(2m_Pb) ≈ 2m_ec² = is the minimum photon energy.
  (b)  (hf/c + m_ec)² - (hf/c)² = m_e²c² + 2hfm_e = (3m_ec)².
  hf = 4m_ec² = is the minimum photon energy.
  (c)  The collision has to conserve energy and momentum.  For a given momentum transfer ∆p, the energy transfer ∆E is much smaller for a massive Pb nucleus than for an electron.