Velocity addition

Problem:

For two inertial coordinate systems K and K' in relative motion at speed "v" along their x₁ axes, the Lorentz transformations provide that
x₁' = γ(x₁ - vt)
x₂' = x₂
x₃' = x₃ and
t' = γ(t - vx₁/c²), where γ = [1 - v²/c²]^-½ .
(a)  Derive the velocity transformations relating speeds u_j (in K) and u_j' (in K'), with j = 1, 2, 3.
(b)  Now assume Kurt (in system K) fires an energetic photon straight up, along his x₂ (or y) axis.  If Paula's system K' travels at v = 0.6 c relative to Kurt, calculate the components of the photon's velocity in Paula's reference frame.
(c)   From your results in part (b), calculate the magnitude of the photon's velocity in Paula's frame.  Explain why this result is to be expected.

Solution:

• Concepts:
  Relativistic kinematics
• Reasoning:
  We are asked to derive the relativistically correct velocity addition formula.
• Details of the calculation:
  (a)  u_i = dx_i/dt, u_i' = dx_i'/dt'
  u₁' = dx₁'/dt' = (dx₁ - vdt)/(dt - (v/c²)dx₁)
  Divide numerator and denominator by dt.
  u₁' = (u₁ - v)/(1 - u₁v/c²)
  Similarly:
  u₂' = γ^-1u₂/(1 - u₁v/c²)
  u₃' = γ^-1u₃/(1 - u₁v/c²)
  (b)  In K: u₁ = 0,  u₂ = c, u₃ = 0.
  In K':  u'₁ = -v = -0.6c,  u'₂ = γ^-1u₂ = 0.8 c, u₃' = 0, 
  (c)  |u'| = (u₁'² + u₂'² + u₃'²)^½ = c.
  This is a postulate of special relativity.

Problem:

A rocket is traveling towards Earth at 0.6 c.  It fires a projectile of mass M with a velocity of 0.8 c in the rocket frame towards Earth.  
(a)  What is the energy of the projectile in the Earth frame?
(b)  Another rocket is traveling at 0.9 c perpendicular to a line from the rocket to Earth and fires a projectile at 0.8 c in the rocket frame and at 90 degrees from the direction of the rocket's motion (in the rocket frame), what is the energy of the projectile in the Earth frame?
(c)  What is the tangent of the angle of the projectile relative to the ship's motion in the Earth frame?

Solution:

• Concepts:
  Relativistic kinematics, velocity addition
• Reasoning:
  The objects move with relativistic speeds.  We are given the relative speed of the objects with respect to a reference frame and must add their velocities to find their speed with respect to each other.
• Details of the calculation:
  Assume that a frame K' is moving with velocity vi with respect to a frame K.  A particle moves in K with velocity u = dr/dt. The particle's velocity in K', u' = dr'/dt', is given by

  u'_|| = (u_|| - v)/(1 - v∙u/c²)
  u_⊥ =  u_⊥/(γ(1 - v∙u/c²))

  where parallel and perpendicular refer to the direction of the relative velocity v.
  (a)  Let K be the rocket frame, K' be the earth fame.  Let the rocket travel into the positive x-direction.
  Then v = -(0.6 c)i, u =  (0.8 c)i, v∙u/c² = -0.48,
  u' = (0.6 + 0.8)c)/(1 + 0.48)i = (0.946 c)i.
  E_projectile = γ_projectile Mc² = 3.08 Mc².
  (b)  Let the rocket travel into the positive y-direction and let it fire the projectile into the positive x direction in its frame.
  Now v = -(0.9 c)j, u =  (0.8 c)i, v∙u/c² = 0, u'_|| = u'_y = 0.9 c, 
  u_⊥ = u'_x = (0.8 c)/γ.
  γ = (1 - v²/c²)^-½ = 2.29,  u'_x = 0.349 c.
  |u'|² = (u'_y² + u'_x²) = 0.93 c².  γ_projectile =3.83, E_projectile = 3.83 Mc².
  (c)  tanθ = u'_x/u'_y = 0.388,  θ = 21^o.

Problem:

A pion, moving along x-axis in the positive x-direction with β = 0.8 in the lab system decays by emitting a muon with β^*  = 0.268 in its own rest frame.
(a)  Find the velocity of the muon (magnitude and direction) in the lab frame if the muon is emitted along the incident direction in the rest system of pion.
(b)  Now assume the muon is emitted along the y-axis in the rest frame of the pion.  Find the velocity of muon in the lab frame.
(c)  Now assume the muon is emitted along the positive y-axis (i.e. perpendicular to the incidental direction of pion in the lab frame).  Find the speed of muon in the lab frame and the direction of emission in the rest frame of pion.  For this part assume β = 0.2

Solution:

• Concepts:
  Velocity addition
• Reasoning:
  A particle moves in K with velocity u = dr/dt.  K' moves with respect to K with velocity v.  The particle's velocity in K', u' = dr'/dt',  is given by
  u'_|| = (u_|| - v)/(1 - v∙u/c²)
  u'_⊥ =  u_⊥/(γ(1 - v∙u/c²))
• Details of the calculation:
  (a)  Here K is the rest frame of the pion, u/c = 0.268 i = β^*i , v/c = -0.8 i = -β i.
  K' is the lab frame.
  u'_||/c_| = (u_||/c - v/c)/(1 - v∙u/c²) = (0.268 + 0.8)/(1 + 0.268 *0.8) = 0.88
  u'_⊥/c = 0
  In the lab frame the muon moves with peed v = 0.88 c in the positive x-direction.
  (b)  Now , u/c = 0.268 j = β^*j , v/c = -0.8 i = -β i.
  u'_||/c_|  = 0.8
  u'_⊥/c = 0.268/γ = 0.268*(1 - 0.64)^½ =  0.161
  v = 0.816 v, tan(θ) = 0.161/0.8 = 0.201,  θ = 11.3^o.
  In the lab frame the muon moves with peed v = 0.816 c in a direction making an angle θ = 11.3^o with the positive x-direction.
  (c)  Here we have u'_|| = (u_|| - v)/(1 - v∙u/c²) = 0.  We need u_|| - v = 0,  u_|| = 0.2 c (-i).
  u_||² +  u_⊥² = (0.268 c)², u_⊥= 0.265 c j.  
  tan θ* = -1.325, 
  In the pion rest frame the muon moves with speed v = 0.268 c in a direction making an angle θ = 127^o with the positive x-direction.
  The speed of the muon in the lab frame is
  u'_⊥ =  u_⊥/(γ(1 - v∙u/c²)) = (0.265 c)(1 - 0.04)^½/(1 - 0.04) = 0.27 c

Problem:

In the reference frame of an outside observer two particles move towards each other, both with relativistic speed v . The angle between them is 2θ as shown in the figure below.  What is the speed of one of the particles as viewed by the other?

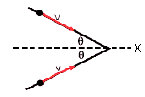
Solution:

• Concepts:
  Relativistic Kinematics, velocity addition
  A particle moves in K with velocity u = dr/dt.  K' moves with respect to K with velocity v.  The particle's velocity in K', u' = dr'/dt',  is given by
  u'_|| = (u_|| - v)/(1 - v∙u/c²),
  u_⊥ =  u_⊥/(γ(1 - v∙u/c²)),
  where parallel and perpendicular refer to the direction of the relative velocity v.
• Reasoning:
  The particles move with relativistic speeds.  We are given the speed of the particles with respect to an inertial frame and are asked to add their velocities to find their speed with respect to each other. 
• Details of the calculation:
  Consider a frame moving with velocity vcos(θ) along the x-axis
  [γ = (1 - (v²/c²)cos²θ)^-½].
  In that frame u'_|| = 0 for each of the particles,
  u_⊥ = ±vsinθ/(γ(1 - (v²/c²)cos²θ)) = ±γ v sinθ,
  the particles approach each other while moving perpendicular to the x'-axis.
  To find the speed of particle 1 (lower particle) in the rest frame of the particle 2 (upper particle) we denote this rest frame by K''.  K'' moves with respect to K' with speed v' = -γ v sinθ, and the particle 1 moves in K' with speed u' = γ v sinθ.
  In K'' particle 1 moves with speed
  u'' = (γ v sinθ + γ v sinθ)/(1 + (γ v sinθ)²/c²) = 2 γ v sinθ/(1 + (γ v sinθ)²/c²),
  with γ = (1 - (v²/c²)cos²θ)^-½.

Problem:

Two spaceships, A and B, are moving along a line in opposite directions.  An observer on Earth measures the speed of spaceship A to be 2*10⁸ m/s and the speed of B to be 1*10⁸ m/s.  
When the captain of spaceship A receives a collision warning, the two ships are separated by 3*10⁹ m according to spaceship A's measurement   How long does spaceship A's captain have to avoid a collision?

Solution:

• Concepts:
  Relativistic kinematics, velocity addition
• Reasoning:
  The objects move with relativistic speeds.  We are given the relative speed of the objects with respect to a reference frame and must add their velocities to find their speed with respect to each other.
• Details of the calculation:
  Let K' be the rest frame of spaceship A and K the rest frame of Earth.  Let spaceship A move in the positive x-direction with respect to Earth.  Spaceship B moves in K with velocity u = -1*10⁸ m/s i.  K' moves with respect to K with velocity v = 2*10⁸ m/s i.  Spaceship B's velocity in K' is
  u'  = (u - v)/(1 - v·u//c²) = -i(2c/3 + c/3)/(1 + 2/9) = -i (9/11) c.
  In K', spaceship B is approaching with speed u' = 0.818 c.  The captain has
  t = d/u' = (3*10⁹ m)/(0.818*3*10⁸ m/s) = 12.22 s to avoid a collision.

Problem:

A spaceship whose rest length is 350 m has a speed of 0.82 c in a certain reference frame.  A micrometeorite, also with a speed of 0.82 c in this same frame, passes the spaceship on an anti-parallel track.  According to an astronaut in the spaceship, how long does it take the micrometeorite to traverse the entire length of the spaceship?

Solution:

• Concepts:
  Relativistic kinematics, velocity addition
• Reasoning:
  The objects move with relativistic speeds.  We are given the relative speed of the objects with respect to a reference frame and must add their velocities to find their speed with respect to each other.
• Details of the calculation:
  Assume our reference frame is moving with velocity -v₁i = -0.82c i with respect to the spaceship.  In our frame the meteorite is moving with velocity -v₂i = -0.82c i.  The velocity addition formula yields v₂₁ = -(v₁+v₂)/(1 + v₁v₂/c²)i = -0.98c i for the velocity of the meteorite in the frame of the spaceship. 
  It takes the meteorite (350 m)/(0.98 c) = 1.19 ms to pass the ship.

Problem:

In reference frame K particle moves with constant velocity u from a source at the origin to a detector located at x = y = z = 10 m in 10^-7 s.
Reference frame K' moves with respect to K with velocity v = 2*10⁸ m/s i.
(a)  What is the speed of the particle in K?
(b)  What is the separation between the source and the detector in K'?
(c)  What is the speed of the particle in K'?

Solution:

• Concepts:
  Relativistic Kinematics
• Reasoning:
  To find the speed of the particle in K', we can use the velocity addition formulas or the Lorentz transformation.
• Details of the calculation:
  (a)  In K, u = (√300)/(10^-7) m/s = 1.732 m/s.
  (b)  v = 2c/3,  γ = 1.8,  d² = 100 + 100 + 100/γ² = 230.9 m², d = 15.2 m.
  (c)  Lorentz transformation:  ct' = γct -γβx.  x' = -γβct + γx,  y' = y,  z' = z.
  Event 1:  The particle leaves the source.  ct' = x' =  y' = z' = 0.
  Event 2:  The particle arrives at the detector. 
  t' = 1.8*(10^-7 s  - (20/3 m)/c) = 1.4*10^-7 s
  x' = 1.8*((-2c/3)(10^-7 s) + 10 m) = -18 m,  y' = z' = 10 m.
  u' = (x'² + y'² + z'²)^½/t' = (22.9 m)/(1.4*10^-7 s) = 1.635*10⁸ m/s = 0.545 c.

Problem:

A space ship is moving to the east at a speed of 0.9c relative to the earth.  A second spaceship is moving to the west at a speed of 0.8c relative to the earth.  What is the speed of one spaceship relative to the other?

Solution:

• Concepts:
  Relativistic Kinematics, velocity addition
• Reasoning:
  The spaceships move with relativistic speeds.  We are given the relative speed of the spaceships with respect to Earth and are asked to add their velocities to find their speed with respect to each other.
• Details of the calculation:
  Earth is moving with velocity v = -0.9c i with respect to 1ocket 1
   In the Earth frame rocket 2 is moving with velocity u = -0.8c i.
  The velocity addition formula u'_|| = (u_|| - v)/(1 - v∙u/c²) yields
  u'_|| = -(0.8c + 0.9c)i/(1 + 0.8*0.9) = -0.99ci.
  The speed of one spaceship relative to the other is 0.99c.

Problem:

A person on Earth observes two rocket ships moving directly toward each other and colliding.  At time t = 0 in the Earth frame, the Earth observer determines that rocket 1, traveling to the right at v₁ = 0.8c, is at point a, and rocket 2 is at point b, traveling to the left at v₂ = 0.6c.  They are separated by a distance 4.2*10⁸ m.
(a)  In the Earth frame, how much time will pass before the rockets collide?
(b)  How fast is rocket 2 approaching in rocket 1's frame?  How fast is rocket 1 approaching in rocket 2's frame?
(c)  How much time will elapse in 1's frame from the time rocket 1 passes point a until collision?  How much time will elapse in 2's frame from the time rocket 2 passes point b until collision?

Solution:

• Concepts:
  Relativistic Kinematics, velocity addition, proper time
• Reasoning:
  The spaceships move with relativistic speeds.  We are given the relative speed of the spaceships with respect to Earth and are asked to add their velocities to find their speed with respect to each other.  We are asked to find the time interval separating two events in the earth frame and then transform to another frame where those two events have the same space coordinate.
• Details of the calculation:
  (a)  0.6ct + 0.8ct = 4.2*10⁸ m.  t = (4.2*10⁸m)/1.4c = 1s is the time that will pass on Earth before the ships collide.
  (b)  Earth is moving with velocity -v₁i with respect to rocket 1.  In the Earth frame rocket 2 is moving with velocity -v₂i. 
  The velocity addition formula yields v₂₁ = -(v₁ + v₂)/(1 + v₁v₂/c²)i = -0.95ci for the velocity of rocket 2 in the frame of rocket 1. 
  Similarly, v₁₂ = 0.95ci.
  (c)  The time interval between passing point a and the collision is the proper time interval in the frame of rocket 1.
  t_ac = t/g₁ = t (1 - 0.8²)^½ = 1 s * 0.6 = 0.6 s.
  The time interval between passing point b and the collision is the proper time interval in the frame of rocket 2.
  t_bc = t/g₂ = t (1 - 0.6²)^½ = 1 s * 0.8 = 0.8 s.

Problem:

A train car of length L' = L₀ in the train's frame of reference moves along a track at velocity v_T = c/2.
A gunman in the rear of car fires a bullet in the direction of motion of the train. 
He observes its velocity to be v_B' = c/2.  For an observer in the rest frame of the track, what are the values of
(a)  L, the length of the car?
(b)  v_B, the velocity of the bullet?
(c)  t₂, the length of time the bullet travels before striking the front of the car?
(d)  x₂, the distance the bullet travels?

 Solution:

• Concepts:
  Lorentz contraction, velocity addition
• Reasoning:
  The train moves with a relativistic speed v_T = c/2 relative to the track.
• Details of the calculation:
  (a)  Lorentz contraction:  γ = (1 - v²/c²)^-½ = 2/√3.  L = L₀/γ = √3L₀/2.
  (b)  Velocity addition:  v_B = (v_B' + v_T)/(1 + v_B'v_T /c²) = (½c + ½c)(1 + ¼) = 4c/5.
  (c)  In the track frame:  v_Bt₂ = L + v_Tt₂,  t₂ = L/(v_B - v_T) = (√3L₀/2)/(3c/10)
  = (5/√3)L₀/c.
  (d)  x₂ = v_Bt₂ = (4c/5)(5/√3)L₀/c = (4/√3)L₀.