First law of thermodynamics and the ideal gas law

Problem:

5 moles of gas in a cylinder undergo an isobaric expansion starting at 293 K.  The cylinder is initially 50 cm tall.  The radius of the cylinder is 10 cm and Δy is 1 cm.  How much work is done by the gas?

Solution:

• Concepts:
  Isobaric expansion, the ideal gas law
• Reasoning:
  The process is isobaric, the pressure P is constant.  If the volume increase from V_initial to V_final, then the work done by the gas is W = P(V_final - V_initial)  
• Details of the calculation:
  W = PΔV = (nRT/V)ΔV = (5*8.31*293/(0.5 π  0.1²) )*(0.01 π 0.1²) J = 243 J

Problem:

One mole of an ideal gas does 3000 J of work on its surroundings as it expands isothermally to a final pressure of 1 atm and volume of 25 L.  Determine
(a)  the initial volume and
(b)  the temperature of the gas.

Solution:

• Concepts:
  Ideal gas law: PV = nRT,  work done on the system: W = -∫PdV
  Energy conservation: ΔU = ΔQ + ΔW
• Reasoning:
  For an isothermal process W = nRT ln(V_i/V_f).
  We are given n, P_final, and V_final, and we are told that the temperature is constant.
• Details of the calculation:
  (a)  For an isothermal process the temperature is constant.  
  Therefore PV = nRT = constant.
  PV = 101000 Pa*25*10^-3 m³ = nRT
  W = nRT ln(V_i/V_f) for an isothermal process.
  W/(nRT) = -3000 J/(101000 Pa*25*10^-3 m³) = -1.19
  (The work done by the gas is -W.)
  V_f/V_i = exp(1.19) = 3.28
  V_i = (25*10^-3 m³)/3.28 = 7.62*10^-3 m³ = 7.62 L
  (b) For an ideal gas PV = nRT.  101000 Pa*25*10^-3 m³ = (8.31 J/K)T.
  T = 303.85 K.

Problem:

A cylinder contains He gas.  In its initial state a the cylinder Volume is V_a = 4.23*10^-3 m³ and the pressure is P_a = 1.19*10^-5 Pa.  The volume is isothermically reduced until the system reaches a state b with V_b = 0.581*10^-3 m³.  This process is followed by an isobaric expansion which allows the system to reach a state c with V_c = V_a.  The cycle finishes with an isochoric or isometric (constant volume) process that brings the system back to state a.
(a)  Draw the cycle in a P-V diagram.
(b)  Find the work done by the system going from b to c.
(c)  Find the work done by the system in one cycle.
(d)  Find the fractional change of the temperature of the system going from b to c.
(e)  When the system goes from c to a, does it absorb or release heat?  Find the amount of heat absorbed or released.
(f)  When the system goes from b to c, does it absorb or release heat?  Find the amount of heat absorbed or released.

Solution:

• Concepts:
  Ideal gas law: PV = nRT,  work done on the system: W = -∫PdV
  Energy conservation: ΔU = ΔQ - ΔW
  increase in internal energy of a system = heat put into the system - work done by the system on its surroundings,
• Reasoning:
  An isothermal process occurs at constant temperature.  P = nRT/V .  Since the internal energy of a gas is only a function of its temperature, ΔU = 0 for an isothermal process.  For the isothermal expansion of an ideal gas we have

  W = ∫_V1^V2PdV = ∫_V1^V2nRT dV/V = nRT∫_V1^V2 dV/V = nRT ln(V₂/V₁).

  W is negative if V₂ < V₁.  Since ΔU = 0, the heat transferred to the gas is ΔQ = W.
  An isobaric is a process that occurs at constant pressure.  We then have

  W = P∫_V1^V2 dV = P(V₂ - V₁).

  If the pressure of an ideal gas is kept constant, then the temperature must increase as the gas expands.  (PV/T = constant.)  Heat must be added during the expansion process.
  An isometric process takes place at constant volume.  Then W = 0 and ΔU = ΔQ.  All the heat added to the system goes into increasing its internal energy.
• Details of the calculation:
  (a) 

  

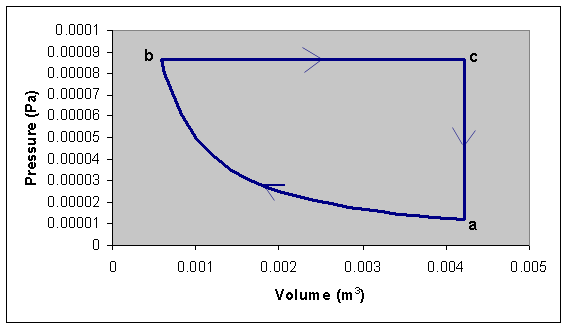
  (b)  W_bc = P_b(V_a-V_b) = P_a(V_a/V_b) (V_a-V_b) = 3.16*10^-7 J,
  U = (3/2)NkT = (3/2)nRT =  (3/2)PV,  ΔU_bc = (3/2)P_b(V_a - V_b) = 4.74*10^-7 J,
  ΔQ_bc = ΔU_bc + W_bc =  4.74*10^-7 J + 3.16*10^-7 J = 7.9*10^-7 J.
  (c)  W_ab = nRT ln(V_b/V_a) = P_aV_a ln(V_b/V_a) = -10^-7 J.  W_cycle = W_bc + W_ab = 2.16*10^-7 J.
  (d)  (T_c - T_b)/T_b = P_b(V_a - V_b)/nRT_b = (V_a - V_b)/V_b = 6.28.  The temperature increases by a factor of 6.2
  (e)  The system releases heat.
  ΔW_ca = 0, ΔU_ca = ΔQ_ca = (3/2)(P_a - P_b)V_a = -4.74*10^-7 J.
  The system releases heat.
  (f)  The system absorbs heat.
  ΔQ_bc = 7.9*10^-7 J.
  [ΔU_ab= 0.  ΔQ_ab = W_ab = nRT ln(V_b/V_a) = -10^-7 J.
  ΔQ_cycle = ΔQ_ab +  ΔQ_bc +  ΔQ_ca =  W_cycle = 2.16*10^-7 J.]

Problem:

Air at 20.0 ^oC in the cylinder of a Diesel engine is compressed from an initial pressure of 1.00 atm and volume of 800 cm³ to a volume of 60 cm³.  Assume that air behaves as an ideal gas with γ  = 1.40 and that the compression is adiabatic.  Find the final pressure and temperature of the air.  (Give numerical answers!)

Solution:

• Concepts:
  Adiabatic processes
• Reasoning:
  We are asked to assume that PV^γ = constant, with γ  = 1.40.
• Details of the calculation:
  This is an adiabatic process where T and P both increase.
  Using P_iV_i ^γ = P_fV_f ^γ we have
  P_f = P_i(V_i/V_f)^γ = (1 atm)(800 cm³/60 cm³)^1.4 = 37.6 atm.
  Since PV = nRT is valid for an ideal gas, and no gas escapes from the cylinder we have
  P_iV_i/T_i = P_fV_f/T_f  --> T_f = [P_fV_f/(P_iV_i)]T_i.
  T_f = = (37.6 atm/ 1atm)(60 cm³/800 cm³)*293 K = 826 K = 553 ^oC.
   

Problem:

A quantity of an ideal monatomic gas consist of N atoms, initially at temperature T₁. 
The pressure and volume are then slowly doubled, in such a way as to trace out a straight line on the P-V diagram. 
In terms of N, k, and T₁, find
(a)  the work done by the gas.
(b)  If one defines an equivalent specific heat capacity (c = ΔQ/ΔT, where ΔQ is the total heat transferred to the gas) for this particular process for the  above monatomic gas, what is its value?

Solution:

• Concepts:
  The P-V diagram, the ideal gas law, the first law of thermodynamics
• Reasoning:
  We are given P₂ = 2 P₁, V₂ = 2 V₁ and asked to find W and ΔQ.
• Details of the calculation:
  
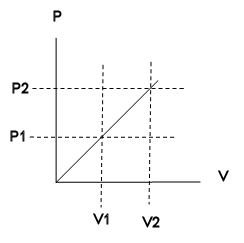
  Given:  P/V = P₁/V₁,     P(V) = (P₁/V₁)V
  Ideal gas law: PV = NkT,   T₂/T₁ = P₂V₂/(P₁V₁) = 4,  T₂ = 4 T₁.
  W = ∫_V1^V2PdV = (P₁/V₁) ∫_V1^V2VdV = ½ (P₁/V₁)(V₂² - V₁²) = (3/2)P₁V₁ = (3/2)NkT₁.
  (b) ΔU = ΔQ - W,  W = work done by the gas.
  ΔQ = ΔU + W
  U = (3/2)NkT,   ΔU = (3/2)NkΔT = (3/2)Nk(T₂ - T₁) =  (3/2)Nk 3T₁ =  (9/2)NkT₁.
  ΔQ = (9/2)NkT₁ + (3/2)NkT₁ = 6NkT₁.
  c = ΔQ/ΔT = 6NkT₁/(3T₁) = 2Nk.

Problem:

Two cylinders A and B, with equal diameters have inside two pistons with negligible mass connected by a rigid rod.
The pistons can move freely.
The rod is a short tube with a valve.  The valve is initially closed.

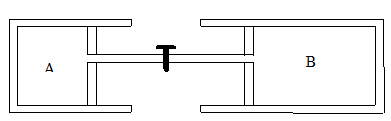
Cylinder A and its piston is adiabatically insulated and cylinder B is in thermal contact with a thermostat which has the temperature T = 27^o C.
Initially the piston of cylinder A is held fixed and cylinder A contains m = 32 kg of argon at a pressure higher than the atmospheric pressure.  Cylinder B contains oxygen at atmospheric pressure (101.3 kPa).
Releasing the piston of cylinder A, it moves slowly (quasi-statically) until it reaches equilibrium.  At equilibrium the volume of the gas in cylinder A has increased by a factor of eight, and in cylinder B the oxygen's density has increased by a factor of 2.  During this process the heat Q = 747.9*10⁴ J is delivered to the thermostat.

(a)  Use the ideal gas law and the first law of thermodynamics to show that for the process taking place in cylinder A we have TV^(2/3) = constant.
(b)  Calculate the parameters P, V, and T of the argon in the initial and final states.
(c)  After equilibrium has been reached, the valve between the cylinders is opened.   Calculate the final pressure of the mixture of the gases.
The kilo-molar mass of argon is 40 kg/kmol.

Solution:

• Concepts:
  The ideal gas law, the first law of thermodynamics
• Reasoning:
  We are asked to track P, V, and T of two quantities of gas.
  Given: 
  Ar:  V₂/V₁ = 8, n = 800 mol.
  O₂:  T₁ = T₂ = 300 K, ρ₁/ρ₂ = 2 --> P₁/P₂ = 2, since P = ρkT and T is constant.
• Details of the calculation:
  (a)  We consider argon an ideal mono-atomic gas.
  For an ideal gas PV = NkT. 
  For an adiabatic process dU = -dW = -PdV. 
  But we also have U = N(3/2)kT for an ideal gas. Therefore we have U = (3/2)PV,
  dU = (3/2)(PdV + VdP). 
  Equating our two expressions for dU we have -PdV = (3/2)(PdV + VdP), 
  dP/P + (5/3)dV/V = 0.  PV^5/3 = constant,  (PV)V^(2/3)= constant,
  TV^(2/3) = constant.
  
  (b)  The oxygen is in contact with a thermostat.  Its temperature and the internal energy are constant. 
  Since the net work done by the gas in the system is zero, the change in the internal energy of the argon is ΔU = Q.
  We have for the argon ΔU = (3/2)nR(T₂ - T₁) = (3/2)nRT₁((V₁/V₂)^(2/3) - 1) = Q.
  T₁ = (2/3)(1/n)(Q/R)(1/((V₁/V₂)^(2/3) - 1)) = (2/3)(1/800)(747.9*10⁴/8.314)(4/3) K = 1000 K.
  T₂ = T_¼ = 250K
  For the oxygen undergoing an isothermal process we have P₁/P₂ = ρ₁/ρ₂.
  P₁ = 1 atm, P₂ = 2 atm = 2.026*10⁵ N/m².
  From the equilibrium condition we have that for the argon P₂ = 2 atm = 2.026*10⁵ N/m².
  For the argon P₁ = P₂(V₂/V₁)(T₁/T₂) = 64 atm = 64.9*10⁵ N/m².
  From the ideal gas law we now have V₁ = nRT₁/P₁ = 1.02 m³,  V₂ = 8V₁ = 8.16 m³.
  So for the Ar gas:
  P₁ = 64.9*10⁵ N/m², V₁ = 1.02 m³, T₁ = 1000 K.
  P₂ = 2.026*10⁵ N/m², V₂ = 8.16 m³, T₂ = 250 K.
  
  (c)  When the valve is opened the gases mix and in thermal equilibrium the final pressure will be P and the temperature T = 27^oC = 300K .  The total number of kilomoles n is constant.  The total volume V of the system is constant.
  n = n_Ar + n_O = PV/(RT)
  Since the density of the oxygen increases by a factor of 2 during the adiabatic expansion of the argon, we know that before the expansion the volume of the oxygen was
  V_{O2 i} = 2*(V_{Ar f} - V_{Ar i}) = 14 V_{Ar i}. 
  The total volume of gas therefore is V = 15 V_{Ar i}.
  The number of moles of oxygen is n_O = (1 atm)*(14 V_{Ar i})/(R 300 K) = 580 mol
  n = n_Ar + n_O = (580 + 800) mol = 1380 mol
  We now have P = nRT/V  = 2.25*10⁵ Pa =  2.2 atm.

Problem:

A container with helium is sealed by a movable heavy piston with cross-sectional area A.  Initially, the piston is in equilibrium, the volume of the gas is V, and the system is in thermal equilibrium with its surroundings. The piston is then slowly lifted by an external force a distance L and held until the thermal equilibrium with the surroundings is re-established.  After that, the container is thermally insulated from the surroundings and piston is released.  Find the new equilibrium position of the piston with respect to its initial position.  Will the piston come to rest or will it oscillate about this position?  Neglect friction, the heat capacities of the piston and the container, and the mass of the gas compared to the mass of the piston.

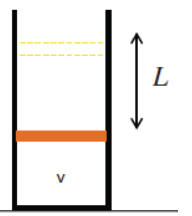
Solution:

• Concepts:
  The first law of thermodynamics, the ideal gas law
• Reasoning:
  The system consists of a container filled with helium gas, which we treat as an ideal, monatomic gas.  The container is sealed by a moveable heavy piston.  Let us consider three separate states of initial, intermediate, and final.
   

  State 1:  Initial

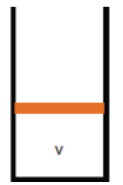  State 2:  Intermediate

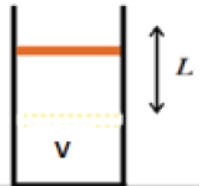  State 3:  Final

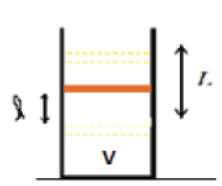  For each state we consider the implications of the ideal gas law, PV = nRT, and the first law of thermodynamics,
  dE_int = dQ - dW,  E_int = (3/2)nRT,  dW = PdV.

• Details of the calculation:
  (1)  The system is initially in equilibrium.  We can apply the ideal gas law to relate the pressure and volume of state 1 to temperature at state 1.
  P₁V = nRT₁,  T₁ = P₁V/(nR)
  Environment:  P_env + Mg/A = P₁, where M is the mass of the piston.
  
  (2)  An external force raises the piston to a distance L.  Heat is supplied by the surrounding thermal reservoir to keep the temperature constant  The change in internal energy between state 1 and state 2 is zero.
  ΔE_int(1 --> 2) = 0. T₂ = T₁.  P₂ = nRT₁/(V + AL).  P₂ < P₁.
  
  (3)  The system is now thermally insulated and the moveable piston is released.  What follows is an adiabatic process, ΔQ = 0.
  The piston will accelerate.  As it accelerates downward, work is done on the gas, resulting in a change in its internal energy and temperature.  The piston will continue to accelerate downward until the pressure P₃ = P₁ = P_env + Mg/A.
  Both the ideal gas law and the fact first law for an adiabatic process yield an expression for T₃/T₁.  We equate these expressions to find the new equilibrium position.
  The ideal gas law implies P₁(V + Al) = nRT₃,  T₃ = P₁(V + Al)/(nR), where l is the distance of the new equilibrium position above the initial position of the piston.  T₃/T₁ = (V + Al)/V.
  As the piston falls the first law of thermodynamics implies dE_int = -PdV = -PAdl'.
  (3/2)nRdT = -PAdl' = -nRT Adl'/(V + Al').
  dT/T = -(2/3)Adl'/(V + Al'),
  ln(T₃/T₁)  = (2/3)ln((V + AL)/(V + Al)),
  T₃/T₁ = ((V + AL)/(V + Al))^(2/3),
  
  (V + Al)/V = ((V+AL)/(V + Al))^(2/3),
  (V + Al)^5/3 = V*(V + AL)^(2/3).
  V + Al = V^3/5*(V + AL)^2/5.
  Al = V^3/5*(V + AL)^2/5 - V.
  If AL << V then Al = (2/5)AL,  l = 2L/5.
  The piston will oscillate.

Problem:

One mole of a monatomic gas is heated in such a way that its molar specific heat is 2R.  During the heating, the volume of the gas is doubled.  By what factor does the temperature of the gas change?

Solution:

• Concepts:
  First law of thermodynamics
• Reasoning:
  dU = dQ - PdV,  where U is the internal energy of the system, P is the pressure, V is the molar volume, and Q is the heat transferred to the gas by the surroundings.  For an ideal gas, U depends on the temperature only, U = 3RT/2.
  Given dQ/dT = 2R, dQ = 2RdT.
• Details of the calculation:
  Using the ideal gas law, PV = RT, we have
  dU = dQ - PdV =  2RdT - (RT/V)dV = (3R/2)dT
  Therefore (RT/V)dV = (R/2)dT, or  2dV/V = dT/T, or V²/T = const.
  Therefore, doubling the volume of the gas will increase its temperature by a factor of four.

Problem:

One mole of an ideal gas undergoes transformations that take it from point A to point B on a p-V diagram by two different paths α and β.  Points A and B have the same temperature T = T₀ (this means that they lie on an isotherm) and the pressure p_A at point A is larger than the pressure p_B at point B.  Path α takes the system from state A to state I through an isochoric (constant volume) transformation, followed by an isobaric (constant pressure) transformation from state I to state B.  Path β takes the system from state A to state II through an isobaric transformation, followed by an isochoric transformation from state II to state B.  Assume that p_A and p_B are known.
(a)  Find V_A and V_B in terms of the known quantities p_A, p_B and T₀.
(b)  In a p-V diagram plot path α and path β
(c)  Assuming that the heat capacities C_V and C_P are constants what is the heat flow into the gas for each path?  Give your results in terms of p_A, p_B, T₀, C_V and C_p.  In each case is heat absorbed or released by the system?  Why?
(d)  In absolute value, for what process is the heat larger?  Why?

Solution:

• Concepts:
  The ideal gas law
• Reasoning:
  We use the ideal gas law together with these definitions:
  at constant pressure:  dQ = nC_PdT
  at constant volume:  dQ = nC_VdT
• Details of the calculation:
  (a)  Ideal gas law:  V_A = RT₀/p_A,  V_B = RT₀/p_B.
  (b)  Points A and B lie on an isotherm.
  
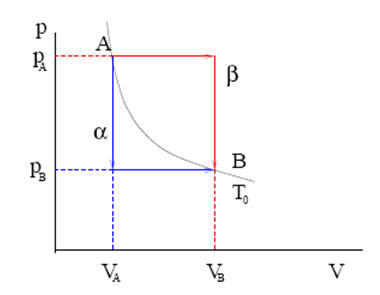
  (c)  For path α:
  ΔQ_α = ∫_T0^T1 C_V dT = ∫_T1^T0 C_P dT = C_V(T₁ - T₀) + C_p(T₀ - T₁) = (T₀ - T₁)(C_P - C_V)
  Here T₁ is the temperature of the state with V_A and p_B.
  T₁ = p_BV_A/R = p_BT₀/P_A.
  Therefore ΔQ_α = T₀(1 - p_B/p_A)(C_P - C_V).
  For path β:
  ΔQ_β = ∫_T0^T2 C_P dT = ∫_T2^T0 C_V dT = C_P(T₂ - T₀) + C_V(T₀ - T₂) = (T₂ - T₀)(C_P - C_V)
  Here T₂ is the temperature of the state with V_B and p_A.
  T₂ = p_BV_AB/R = p_AT₀/P_B.
  Therefore ΔQ_β = T₀(p_A/p_B - 1)(C_P - C_V).
  Since C_p > C_v, heat is absorbed in each case.
  (d)  |Q_β| > |Q_α|
  The internal energy of the system is the same at points A and B since the temperature is the same.  The heat absorbed along a path is therefore equal to the work done by the system along that path,  W_β = p_A(V_B - V_A),  W_α = p_b(V_B - V_A), 
  |Q_β|/|Q_α| = W_β/W_α = p_A/p_B.

Problem:

A horizontal insulated cylinder is partitioned by a frictionless insulated piston which prevents heat exchange between the two sides.  On each side of the piston we have 30 liters of an ideal monatomic gas at a pressure of 1 atmosphere and a temperature of 300 K.  Heat is very slowly injected into the gas on the left, causing the piston to move until the gas on the right is compressed to a pressure of 2 atmosphere.
(a)  What are the final volume and temperature on the right side?
(b)  What are the final values of P, V, and T on the left side?
(c)  What is the change in the internal energy for the gas on the right side?  How much heat did it absorb and how much work was done on it?
(b)  What is the change in the internal energy for the gas on the left side?  How much heat did it absorb and how much work was done on it?

Solution:

• Concepts:
  Ideal gas law: PV = nRT,  work done by the system: W = +∫PdV
  Energy conservation: ΔU = ΔQ - ΔW, adiabatic processes:  PV^γ = constant
• Reasoning:
  The gas on the right side is compressed adiabatically.  The pressure on both sides is the same and the total volume of the left plus the right side is constant.
• Details of the calculation:
  (a)  Since the compression is adiabatic, PV^γ = constant. 
  For an ideal monatomic gas γ = 5/3.
  V_{f r}= V_i(P_i/P_fr)^1/γ = 30 liter * (0.5)^3/5 = 19.8 liter ≈ 20 liters.
  From the ideal gas law T^γ/P^γ-1 = constant, T_{f r}= T_i(P_fr/P_i) ^γ-1/γ = 300 K * 2^2/5 ≈ 396 K.
  (b)  The mechanical equilibrium implies P_f = 2 atm, the same as on the right side.
  V_fl = 2V_i - V_fr ≈ 40 liters.  Then, from the ideal gas law, T_fl  = 300 K*(PV)_fl/(PV)_i ≈ 800 K.
  (c)  ΔU = (3/2)nRΔT.  nR = P_iV_i/T_i.  ΔU = (3/2)P_iV_i(T_fr - T_i)/T_i ≈ 14.4 atm-liter.
  The gas on the right side did not absorb any heat, since it was compressed adiabatically.
  ΔQ = 0, ΔW = -14.4 atm-liter.  Work is done on the gas.
  (d)  For the left side ΔU = (3/2)nRΔT = (3/2)P_iV_i(T_fl - T_i)/T_i ≈ 75 atm-liter.
  ΔW = 14.4 atm-liter, since the left and right side are always in mechanical equilibrium.
  The gas does work.
  ΔQ = ΔU + ΔW ≈ 75 atm-liter is the amount of heat absorbed by the gas.

Problem:

Let C_P and C_V denote the molar specific heat of an ideal gas at constant pressure and at constant volume, respectively.  Show that C_P - C_V = R.

Problem:

Let C_P and C_V denote the molar specific heat of an ideal diatomic gas at room temperature at constant pressure and constant volume, respectively.  Find the ratio C_P/C_V.