Entropy involving ideal gases

Problem:

Calculate the entropy change of an ideal gas that undergoes a reversible isothermal expansion from volume V₁ to V₂.

Solution:

• Concepts:
  Isothermal processes
• Reasoning:
  For an ideal gas PV = nRT.
  For an isothermal process PV = constant, dU = dQ - dW = 0. dQ = dW = PdV.
• Details of the calculation:
  dS = dQ/T = PdV/T.  ΔS = (1/T) ∫₁²PdV = (nR) ∫₁²(1/V)dV = nRln(V₂/V₁).

Problem:

Calculate the entropy change of 1 mole of an ideal gas that undergoes an isothermal transformation from an initial state of pressure 1.5 atm and a volume of 500 cm³ to a final state of pressure 0.90 atm.

Solution:

• Concepts:
  Isothermal processes
• Reasoning:
  For an ideal gas PV = nRT.
  For an isothermal process PV = constant, dU = dQ - dW = 0, dQ = dW = PdV.
• Details of the calculation:
  dS = dQ/T = PdV/T.  ΔS = (1/T) ∫_A^BPdV = (nR) ∫_A^B(1/V)dV = nRln(V_B/V_A)
  = nRln(P_A/P_B).
  Here n = 1, ΔS = 8.31 * ln(1.5/0.9) J/K = 4.2 J/K.

Problem:

One mole of an ideal gas is compressed at 60 ^oC isothermally from 5 atm to 20 atm.
(a)  Find the work done.
(b)  Find the entropy change for the gas and interpret its algebraic sign.
Gas constant : 8.314 J/(mol K)

Solution:

• Concepts:
  Ideal gas law: PV = nRT,  work done on the system: W = -∫PdV
  Energy conservation: ΔU = ΔQ + ΔW
  Change in entropy:   ΔS = ∫_i^f dS = ∫_i^f dQ_r/T
  The subscript r denotes a reversible path.
• Reasoning:
  Using the ideal gas law we can find the work done on the system.  Using ΔU = ΔQ + ΔW we can then find the amount of heat transferred to or from the system.  Knowing ΔQ allows us to calculate ΔS.
• Details of the calculation:
  (a)  The temperature is constant: 
  -∫PdV = -nRT∫(1/V)dV = nRT ln(V_i/V_f) = nRT ln(P_f/P_i) =  RT ln(4).
  W = (8.314 J/K) * (333 K) ln(4) = 3838 J.
  (b)  Energy conservation:
  increase in internal energy of a system
  = heat put into the system + work done on the system by its surroundings,
  or  ΔU = ΔQ + ΔW.
  The temperature stays constant, the internal energy stays constant.  The work done on the system is positive, therefore ΔQ = - ΔW is negative. 
  ΔS = ΔQ/T = (-3838 J)/(333 K) = -11.5 J/K

Problem:

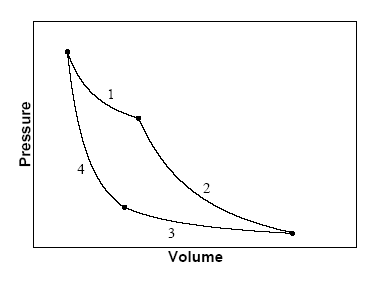
The figure below shows a maximally efficient Carnot cycle in the pressure-volume plane for a heat engine operating between two heat reservoirs to perform work.
(a)  For each label 1 through 4 identify the process, say whether work is done by the working fluid or on it and whether heat is added to the working fluid or extracted from it.
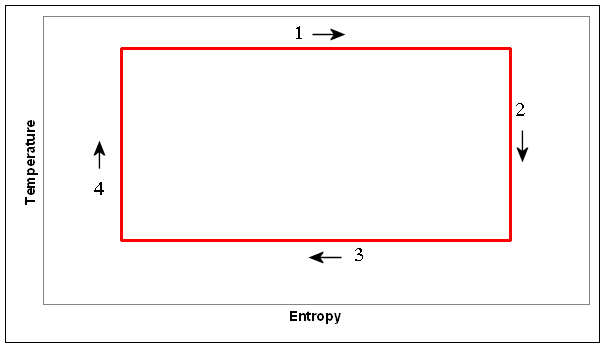
(b)  Make a diagram showing the same cycle in the temperature-entropy plane.  Label the parts of your diagram that correspond to the parts labeled in the P-V diagram and put arrows on each segment indicating the direction it is traversed.

Solution:

• Concepts:
  The Carnot cycle, isothermal and adiabatic processes, entropy.
• Reasoning:
  We are asked to describe the Carnot cycle in various ways.
• Details of the calculation:
  (a)
  (1)  Isothermal expansion:  The engine is in contact with a heat reservoir at temperature T₁.
  The engine does work.  ΔW = ∫PdV.  Heat is added to the working fluid.
  (2)  Adiabatic expansion:  During the expansion the temperature falls to T₂.
  The engine does work.  ΔW = ∫PdV.  No heat is added or extracted from the working fluid.
  (3)  Isothermal compression:  The engine is in contact with a heat reservoir at temperature T₂.
  Work is done on the engine.  ΔW = -∫PdV.   Heat is extracted from the working fluid.
  (4)  Adiabatic compression:  During the compression the temperature rises to T₁.
  Work is done on the engine.  ΔW = -∫PdV.  No heat is added or extracted from the working fluid.
  (b)
  Change in entropy: ΔS = ∫_i^f dS = ∫_i^f dQ_r/T
  The subscript r denotes a reversible path.
  

Problem:

A cylinder is partitioned by a membrane into a volume V₁ initially filled with a classical ideal gas of N particles with no internal degrees of freedom at temperature T, and a volume V₂ initially enclosing a perfect vacuum.
(a)  The cylinder is in contact with a heat reservoir at temperature T.  The membrane is moved slowly without friction, allowing the gas to fill the entire cylinder.  Compute the work done by the gas, the heat transferred between the gas and the heat bath, and the change in the entropy of the gas.  Is this a reversible process?
(b)  The cylinder is returned to its initial state and insulated from the heat bath.  The membrane is allowed to break, releasing the gas to fill the entire volume.  Assume that the expansion occurs essentially instantaneously, and a  new equilibrium is reached.  Compute the work done by the gas and the change in the entropy.  Is this a reversible process?

Solution:

• Concepts:
  Entropy, energy conservation, the ideal gas law
• Reasoning:
  Change in entropy: ΔS = ∫_i^f dS = ∫_i^f dQ_r/T, where the subscript r denotes a reversible path.
  Isothermal expansion can be a reversible process.  For isothermal expansion ΔS = ΔQ_r/T.
  We calculate the entropy change for a reversible isothermal expansion.
  Since entropy is a state function, this entropy change also applies to an irreversible isothermal expansion.
  We find ΔQ using energy conservation and the ideal gas law.
• Details of the calculation:
  (a)  The work done by the gas is W = ∫PdV.
  PV = NkT.  The temperature is constant so P = constant/V.
  W = NkT∫(1/V)dV = NkT ln(V_f/V_i) = NkT ln(1 + V₂/V₁).
  ΔU = ΔQ - ΔW.  U = internal energy, Q = heat put into the system, W = work done by the system.
  ΔU = 0, since the temperature is constant.
  ΔQ = ΔW = NkT ln(1 + V₂/V₁).
  ΔS = ΔQ_r/T = Nk ln(1 + V₂/V₁).
  Although the entropy change is the same, the process described is not a reversible process.  An expansion is reversible only when the pressure of the gas inside and outside are the same during all stages of the expansion.  Only in this case could an infinitesimal change in pressure reverse the direction of the expansion (i.e., resulting in compression).
  
  (b)  The temperature is proportional to the average kinetic energy of the atoms.  The average kinetic energy of the atoms does not change, so T stays constant.  No work is done by the gas, no heat is transferred to or from the gas.  The change in entropy depends only on the initial and final state.  These states are the same as in part (a).
  ΔS = Nk ln(1 + V₂/V₁). 
  This is not a reversible process.

Problem:

Consider a system of one mole of an ideal gas A and three moles of an ideal gas B at the same pressure P and temperature T, in volumes of V_A and V_B respectively.  The two gases are separated by a partition so they are each sequestered in their respective volumes.  If the partition is removed, calculate the change in entropy of the system.

Solution:

• Concepts:
  Entropy, the ideal gas law
• Reasoning:
  Change in entropy: ΔS = ∫_i^f dS = ∫_i^f dQ_r/T, where the subscript r denotes a reversible path.
  The gases will mix.  To calculate the entropy change, we treat the mixing as two separate gas expansions, one for gas A and another for gas B.
  Here we have and expansion at constant temperature.  For a reversible path leading from the initial to the final state for each gas
  dU = 0, dQ = PdV = nRTdV/V,  dS = nRdV/V.
• Details of the calculation:
  For each gas ∆S = nRln(V_f/V_i).  So for the two separate gas expansions we have
  ∆S_A = n_ARln((V_A + V_B)/V_A),  ∆S_B = n_BRln((V_A + V_B)/V_B).
  The total entropy change is 
  ∆S = ∆S_A + ∆S_B = n_ARln((V_A + V_B)/V_A) +  n_BRln((V_A + V_B)/V_B).
  PV = nRT implies that the initial volume is directly proportional to the number of moles.  Therefore  ∆S = n_ARln((n_A + n_B)/n_A) +  n_BRln((n_A + n_B)/n_B).
  ∆S_mix = Rln(4) + 3Rln(4/3) = 2.25 R = 18.7 J/K.