Thermal expansion and conductivity

Problem:

A mercury thermometer has a bulb of volume 0.100 cm³ at 10^oC.  The capillary tube above the bulb has a cross-sectional area of 0.012 mm².  The volume thermal expansion coefficient of mercury is 1.8*10^-4 (^oC)^-1.  How much will the mercury rise when the temperature rises by 20^oC?

Solution:

• Concepts:
  The volume expansion coefficient
  The average volume expansion coefficient b is defined through ΔV = βVΔT. 
• Reasoning:
  The volume of the mercury will increase as the temperature rises and the mercury will rise in the capillary tube.
• Details of the calculation:
  The increase in temperature is 20^oC.  The change in the volume of the mercury is 
  ΔV = βVΔT = (1.8*10^-4 (^oC)^-1)(0.100 cm³)(20 ^oC) = 3.6*10^-4 cm³ = 0.36 mm³.
  Δh = ΔV/A = (0.36 mm³)/(0.012 mm²) = 30 mm.
  The mercury will rise 30 mm.

Problem:

A bar of gold is in thermal contact with a bar of silver of the same length and area.  One end of the compound bar is maintained at 80 ^oC and the opposite end is at 30 ^oC.  When the heat flow reaches steady state, find the temperature at the junction.
The thermal conductivity of gold is 314 W/(m^oC), and the thermal conductivity of silver is 427 W/(m^oC).

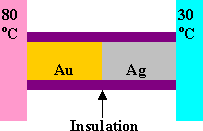
Solution:

• Concepts:
  Thermal conductivity
  The thermal conductivity k is defined through the equation ΔQ/Δt = -kA ΔT/Δx.
• Reasoning:
  When a steady state is reached, then the same amount of heat crosses any cross sectional area perpendicular to the bar per second.  (Otherwise the energy would increase in certain regions, the temperature would increase there, the temperature gradient would change, and we would not have a steady state.)   The amount of heat flowing is determined by the temperature difference and the thermal conductivity.
• Details of the calculation:
  If the temperature at the junction is T, then in the gold we have
  ΔQ/Δt = (314 W/(m^oC))*A*(80 ^oC - T)/(L/2)
  and in the silver we have
  ΔQ/Δt = (427 W/(m^oC))*A*(T - 30 ^oC)/(L/2).
  We can therefore write
  (314 W/(m^oC))*A*(80 ^oC - T)/(L/2) = (427 W/(m^oC))*A*(T - 30^oC)/(L/2).
  (314 W/(m^oC))*(80 ^oC - T) = (427W/(m^oC))*(T - 30 ^oC).
  (80 ^oC - T) = 1.36*(T - 30 ^oC).
  120.8 ^oC = 2.36 T.
  T = 51.2 ^oC.

Problem:

A Thermopane window of area 6 m² is constructed of two layers of glass, each 4 mm thick, separated by an air space of 5 mm.  If the inside is at 20 ^oC and the outside is at -30 ^oC, what is the rate of heat loss through the window?
Thermal conductivity of Thermopane: 0.8 W/(m^oC)
Thermal conductivity of air: 0.0234 W/(m^oC)

Solution:

• Concepts:
  Thermal conductivity
  The thermal conductivity k is defined through the equation.
• Reasoning:
  When a steady state is reached, then the same amount of heat crosses any cross sectional area perpendicular to the bar per second.  (Otherwise the energy would increase in certain regions, the temperature would increase there, the temperature gradient would change, and we would not have a steady state.)   The amount of heat flowing is determined by the temperature difference and the thermal conductivity.
  ΔQ/Δt = -kA ΔT/Δx.
• Details of the calculations
  When a steady state is reached, then the same amount of heat crosses any cross sectional area per second.  Let the temperature of the inner glass-air boundary be T₁ and the temperature of the outer glass-air boundary be T₂. Then for the inner piece of glass we have
  ΔQ/Δt = (0.8 W/(m^oC))*6 m²*(20 ^oC - T₁)/0.004 m.
  For the air layer we have
  ΔQ/Δt = (0.0234 W/(m^oC))*6 m²*(T₁ - T₂)/0.005 m.
  For the outer piece of glass we have
  ΔQ/Δt = (0.8 W/(m^oC))*6 m²*(T₂ + 30 ^oC)/0.004 m.
  We have 3 equations for three unknowns, ΔQ/Δt, T₁, and T₂.
  The first and third equation yield (20 ^oC- T₁) = (T₂ + 30 ^oC), T₂ = -10^oC - T₁.
  Inserting this expression for T₂ into the second equation we have
  ΔQ/Δt = (0.0234 W/(m^oC))*6 m²*(2 T₁+10 ^oC)/0.005 m.
  Combining this equation with the first equation then yields
  (0.0234 W/(m^oC))*(2 T₁+10 ^oC)/0.005 m = (0.8 W/(m^oC))*(20^o C - T₁)/0.004 m.
  0.0234*(2 T₁+10 ^oC) = 20 ^oC - T₁.
  1.0468 T₁ = 19.776 ^oC. T₁ = 18.882 ^oC.
  The first equation now yields
  ΔQ/Δt = (0.8 W/(m^oC))*6 m²*(1.118 ^oC)/0.004 m = 1.34 kW.