Static and flowing fluids
Static fluids
Problem:
What is the hydrostatic force on the back of Grand Coulee Dam if the water in
the reservoir is 150m deep and the width of the dam is 1200m.

Solution:
- Concepts:
The relationship between force and pressure
The pressure
at a point below the surface of a liquid at rest in a constant gravitational
field depends only on the depth d of that point and the pressure at the
surface.
P = P0 + ρgd.
- Reasoning:
The water behind the dam at rest.
- Details of the calculation:
Let us denote the distance below the
surface by y. The pressure on the side of the dam facing the water at depth
y is P0 + ρgy. Here P0 is the atmospheric pressure
(101 kPa) and ρ is the density of water. The force on a surface element of
width w and height dy at depth y is
dF = (P0 + ρgy)dA = (P0
+ ρgy)wdy.
The total force on this side of the dam points outward
and has magnitude
∫0150 dF = wP0∫0150
dy + wρg∫0150 ydy = wP0150 + wρg1502/2.
(All quantities are measured in SI units.)
The total force on the side of
the dam facing air is wP0150, inward. The net force on the dam
is F = wρg1502/2, outward. With w = 1200m and ρ = 1000kg/m3,
F = 1.32*1011N.
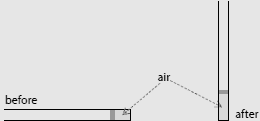
Problem:
A pipe of length 180 m, open on one end and closed on the other, lies at the
bottom of a 200 m deep lake. A light movable piston is placed inside the
pipe. The space between the closed end of the pipe and the piston is
filled with air. The piston is in equilibrium 20 m away from the closed
end of the pipe.
The open end of the pipe is very slowly raised until the
pipe is brought into the vertical position, its closed end resting at the bottom
of the lake.
What is the height of the air column inside the vertical pipe?
Neglect the atmospheric pressure and assume the water temperature is the
same throughout the lake.
Solution:
- Concepts:
The ideal gas law, pressure in a liquid as a function of
depth
- Reasoning:
In equilibrium the air pressure in the pipe equals the
water pressure, Pwater = ρwatergd, neglecting the
atmospheric pressure. Here d is the depth below the surface of the water.
- Details of the calculation:
Before: Pwater = ρwaterg*200
m = nkT/(A 20 m).
Here A is the cross-sectional area of the pipe.
nkT/A = ρwaterg*4000 m2 = constant.
After: ρwaterg*(200
m - h) = nkT/(A h).
nkT/A = ρwaterg*(200 m - h)h.
4000 m2
= (200 m - h)h.
h = (100 ± √6000) m.
h = (100 - 20*√15) m = 22.5 m.
Only the solution h = 100 - 20*√15 represents a stable equilibrium.
d(Pwater(h)
- Pair(h))/dh must be positive for a stable equilibrium to exist.
d(Pwater - Pair)/dh = -ρwaterg + nkT/(Ah2)
= ρwaterg*(4000 m/h2 - 1).
For h = (100 - 20*√15)
m, d(Pwater - Pair)/dh is positive but for h = (100 +
20*√15) m it is negative.
Flowing fluids
Problem:
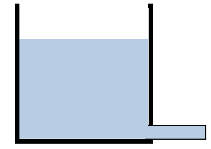
A
cylindrical vessel of radius R = 0.1 m is filled with a liquid to a height of 0.5
m. It has a capillary tube 0.15 m long and radius r = 0.0002 m fixed
horizontally at its bottom. Find the time in which the water level will fall to
a height of 0.2 m. Assume an ideal fluid in a frictionless environment.
Solution:
- Concepts:
Bernoulli's equation and the continuity equation
- Reasoning:
We have an ideal incompressible fluid
- Details of the calculation:
We
introduce points B and C as shown in the figure below.
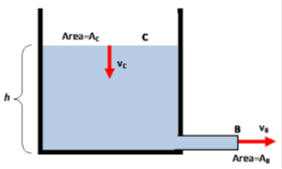
The
velocities at these two points are vC and vB.
The
continuity equation yields vCAC = vBAB.
AC = πR2 = 0.0314 m2, AB = πr2
= 1.3*10-7 m2.
vC = 4*10-6 vB.
The
velocity of liquid at point C is much smaller than the velocity of the liquid at
point B.
The
pressure at points B and C is atmospheric pressure. Bernoulli's equation
therefore yields
ρgh + ρvC2/2 = ρvB2/2.
Since vC << vB then we have ρgh = ρvB2/2,
vB = (2gh)½, vC = 4*10-6 (2gh)½.
We also
have vC = -dh/dt.
-dh/dt = 4*10-6 (2gh)½, -dh/h½ = = 4*10-6
(2g)½dt,
∫0.20.5 = 1.8*10-5 t, 2(0.5½ -
0.2½) = 1.8*10-5 t, t = 2.9*104 s = 8 h.
Problem:
The volume flow rate of water through a horizontal pipe is 2 m3/min.
Determine the speed of flow at a point where the diameter of the pipe is
(a)
10 cm,
(b) 5 cm.
Solution:
- Concepts:
The equation of continuity
- Reasoning:
Area 1 * v1 = Area 2 * v2, since
water is incompressible.
- Details of the calculation:
Al = V. Adl/dt = dV/dt =
volume flow rate. (A is the cross-sectional area and l is the
length of a section of pipe.)
dl/dt = v = flow speed.
(πd2/4)v
= 2 m3/60 s. v = (0.042/d2) m/s with d measured in m.
d = 10 cm: v = 4.24 m/s,
d = 5 cm: v = 16.98 m/s
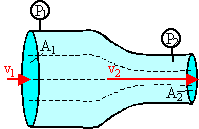
Problem:
A Venturi tube may be used as a fluid flow meter. If the difference in
pressure P1 - P2 = 21 kPa, find the fluid flow rate in m3/s
given that the radius of the outlet tube is 1 cm, the radius of the inlet tube
is 2 cm, and the fluid is gasoline (ρ = 700 kg/m3).
Solution:
- Concepts:
Bernoulli's equation: P + ρgh + ½ρv2 = constant.
- Reasoning:
If we neglect friction, we have a conservative system. Bernoulli's equation
is derived assuming the mechanical energy of the system is conserved. If a
fluid or a gas, which is not being compressed, is flowing in a steady state,
then the pressure depends on the speed of the fluid or the gas. The faster
the fluid is flowing, the lower is the pressure at the same height.
- Details of the calculation:
P1 + ρgh1 + ½ρv12 = P2
+ ρgh2 + ½ρv22.
h is constant, so P1 + ½ρv12 = P2
+ ½ρv22.
P1 - P2 = ½ρv22 - ½ρv12.
21 kPa = (350 kg/m3)(v22 - v12).
From the equation of continuity we have Area 1 * v1 = Area 2 * v2.
v1 = (A2/A1)v2.
Inserting this into the above equation we have(1 - (A2/A1)2)v22
= (21000/350)(m/s)2.
(A2/A1)2 = ¼2 = 1/16. v22
= (21000/350)(16/15)(m/s)2 = 64 (m/s)2.
v2 = 8 m/s.
The fluid flow rate therefore is v2A2 = (8 m/s)π(0.01
m)2 = 0.0025 m3/s.
Problem:
Water circulates throughout a house in a hot-water heating system. If
the water is flowing at a speed of 0.2 m/s through a 5.0 cm-diameter pipe in the
basement under a pressure of 3.0 atm, what will be the flow speed and pressure
in a 1 cm-diameter pipe on the second floor 5.0 m above the basement?
Assume the pipes do not divide into branches. (1 atm = 101 kPa)
Solution:
- Concepts:
Bernoulli's equation: P + ρgh + ½ρv2 = constant
The equation of continuity: Area 1 * v1 = Area 2 * v2.
- Reasoning:
If we neglect friction, we have a conservative system.
Bernoulli's equation is derived assuming the mechanical energy of the system
is conserved. If a fluid or a gas, which is not being compressed, is
flowing in a steady state, then the pressure depends on the speed of the
fluid or the gas. The faster the fluid is flowing, the lower is the
pressure at the same height.
- Details of the calculation:
P1 + ρgh1 + ½ρv12
= P2 + ρgh2 + ½ρv22.
P2
= P1 + ρg(h1 - h2) + ½ρ(v12
- v22).
v2 = v1*25 = 5
m/s.
v12 - v22 = -24.96
(m/s)2.
P2 - P1 = -1000 kg/m3*9.8
m/s2*5 m - 500 kg/m3*24.96 (m/s)2 = -61480
Pa.
1 atmosphere = 101 kPa.
P2 = (3 - 0.61) atm = 2.39 atm
= 241 kPa.





