Buoyancy (gases)
Problem:
The mass of a hot air balloon and its cargo (not including the air inside) is
200 kg. The air outside is at 10 oC and 101 kPa. The
volume of the balloon is 400 m3. To what temperature must the
air in the balloon be heated before the balloon will lift off. (Air
density at 10 oC is 1.25 kg/m3.)
Solution:
- Concepts:
The buoyant force
- Reasoning:
For the balloon to lift off, the buoyant force B must be
greater than its weight.
- Details of the calculation:
The buoyant force is equal to the weight
of the displaced air at 10 oC = 283 K. B = (1.25 kg/m3)(400
m3)(9.8 m/s2) = 4900 N. The weight of the balloon is
200 kg(9.8 m/s2) + weight of hot air. The hot air therefore must
weigh less than 4900 N - 1960 N = 2940 N. Its mass must be less than 2940
N/(9.8 m/s2) = 300 kg. Its density must be less than r = 300
kg/(400 m3) = 0.75 kg/m3.
At constant pressure, the
volume of a gas is proportional to the absolute temperature. (Law of
Gay-Lussac) The pressures on the inside and outside of the inflated balloon
are nearly equal. The pressure on the outside is the constant atmospheric
pressure. The Law of Gay-Lussac therefore applies.
Since the volume of a
gas at constant pressure is proportional to its temperature, its density ρ =
m/V is proportional to 1/T.
We have ρ1/ρ2 = T2/T1.
ρ1T1/ρ2 = T2. (1.25 kg/m3)(283
K)/(0.75 kg/m3) = 472 K = T2.
The air in the
balloon must be heated to more than 472 K = 199 oC.
Problem:
Two balloons have been filled up with air under atmospheric
pressure to volumes V1 and V2, respectively. They
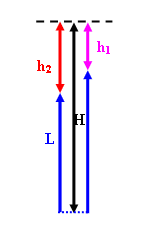
are now submerged under water. A thin string of length L, which is run
through a pulley at a fixed depth H, connects the balloons. (The radii of
the pulley and the balloons are much smaller than the length of the string.)
By setting the initial positions of the balloons, one can achieve a state of
equilibrium. Neither balloon is rising or going down. Determine the
difference in the depth of the balloons (in terms of H and L) under those
conditions. The mass of the balloon skins, of the string, and of the air
is negligible. The temperature of the water is constant and equal to the
temperature of the air.
Solution: