Buoyancy (liquids)

Problem:

Near the surface of a planet like Earth but with no atmosphere a small solid sphere of mass m and density ρ = ½ρ_water is held near the center of a large box filled with water on top of a high tower.  The box and the sphere are released simultaneously.
(a)  What are the force of gravity Fg acting on the sphere, the net force F_net acting on the sphere, and the acceleration a of the sphere?
(b)  If only the sphere is released, but the box is held fixed, what, initially, are the force of gravity F_g acting on the sphere, the net force F_net acting on the sphere, and the acceleration a of the sphere?
(c)  In case (b), if we set F_g = m*a, what is the effective mass m* of the sphere?

Solution:

• Concepts:
  Newton's 2nd law, gravity. the buoyant force
• Reasoning:
  Only gravity is acting on the freely falling sphere, while gravity and the buoyant force act on the sphere in the fixed pool.
• Details of the calculation:
  (a)  F_g = F_net = mg,  where g points towards the surface, a = g = 9.8 m/s² downward.
  (b)  F_g =  mg,  F_net = mg + B = mg - 2mg = - mg.  Here B is the buoyant force, B = -2mg,
  B points upward.  a = F_net/m = -g, upward.
  (c)  F_g =  mg = m*a = -m*g.  m* = -m, the effective mass is negative.

Problem:

A Styrofoam slab has a thickness h and a density ρ_object.  What is the area of the slab, if it floats with its top surface just awash in fresh water when a swimmer of mass m is on top?

Solution:

• Concepts:
  The buoyant force
• Reasoning:
  When an object floats, the magnitude of the buoyant force is equal to the magnitude of its weight.
• Details of the calculation:
  The magnitude of the buoyant force is equal to the magnitude of the weight w_water of the displaced water.  w_water = ρ_waterAhg, where A is the area of the slab. 
  The the magnitude of the weight of the object is  w_object = ρ_objectAhg + mg.  
  We need w_water = w_object.
  ρ_waterAhg = ρ_objectAhg + mg.
  ρ_waterAh - ρ_objectAh = m.
  A = m/(ρ_waterh - ρ_objecth)

Problem:

A frog in a hemispherical pod finds that he just floats without sinking into a sea of blue-green ooze with density 1.35 g/cm³.  If the pod has radius 6 cm and negligible mass, what is the mass of the frog?

Solution:

• Concepts:
  The buoyant force
• Reasoning:
  When an object floats, the magnitude of the buoyant force is equal to the magnitude of its weight.
• Details of the calculation:
  The magnitude of the buoyant force is equal to the the magnitude of the weight w_liquid of the displaced liquid.
  w_liquid = ρ_liquidVg.
  The volume V of the displaced liquid is the volume of one half sphere, 
  V = 2πr³/3 = 2π(6cm)³/3 = 452cm³.
  The magnitude of the weight of the object is w_object = m_frogg.  (We are neglecting the weight of the air-filled pod.)
  ρ_liquidVg = m_frogg. 
  m_frog = 1.35(g/cm³)452cm³ = 610g.

Problem:

A beaker of mass 1 kg containing 2 kg of water rests on a scale.  A 2 kg block of aluminum (specific gravity of 2.7) is suspended from a spring scale and is submerged in the water.
(a)  What does the upper spring scale read for the weight of the aluminum block?
(b)  What does the lower scale read for the weight of the whole system?

Solution:

• Concepts:
  Buoyancy
• Reasoning:
  An object partially or wholly immersed in a gas or liquid is acted upon by an upward buoyant force B equal to the weight w of the gas or liquid it displaces.  B = w.
• Details of the calculation:
  (a)  The scale reads the weight of the block minus the buoyant force acting on the block.
  F_{upper scale} = (m_AL - ρ_WV_AL)g = m_AL(1 - ρ_W/ρ_AL)g.
  ρ_AL = 2.7 ρ_W.
  F_{upper scale} =  (2 kg*9.8 m/s²)(1 - 1/2.7) = 12.34 N.
  (b)  Newton's third law
  F_{lower scale} =  (m_W + m_beak + ρ_WV_AL)g = (m_W + m_beak + m_ALρ_W/ρ_AL)g
  =  (3 kg + 2 kg/2.7)* 9.8 N = 36.66 N.

Problem:

A polar bear partially supports herself by pulling part of her body out of the water onto a rectangular slab of ice of volume 10 m³.  The ice sinks down so that only half of what was once exposed now is exposed, and the bear has 60% of her volume (and weight) out of the water.  Assume that the bear and the water have mass density 1 g/cm³ and ice has mass density 0.9 g/cm³.  Estimate the bear's mass.

Solution:

• Concepts:
  The buoyant force
• Reasoning:
  An object partially or wholly immersed in a gas or liquid is acted upon by an upward buoyant force B equal to the weight w of the gas or liquid it displaces.
• Details of the calculation:
  B = W
  Without the bear:
  Let f denote the fraction of the ice that is exposed.
  B = (1 - f)(10 m³)*(1000 kg/m³)*g = (1 - f)(10000 kg)*g.
  W = (10 m³)*(900 kg/m³)*g = (9000 kg)*g.
  (1 - f)10000 = 9000, f = 1- 9/10 = 0.1.
  Without the bear the exposed fraction is 0.1.

  With the bear:
  B = (1 - f/2)(10 m³)*(1000 kg/m³)*g = (9500 kg)*g.
  W = (9000 kg)*g + 0.6*m_bear*g.
  0.6*m_bear = 500 kg,  m_bear = 833 kg.

Problem:

A thin vertical uniform wooden rod is pivoted at the top and immersed in water as shown.

The pivot point is slowly lowered.  At a certain moment the rod begins to deflect from the vertical.  What fraction of the rod is still in the water at that moment if the density of the rod is one-half of the density of water?

Solution:

• Concepts:
  The buoyant force, stable versus unstable equilibrium
• Reasoning:
  If the rod is displaced by a small angle θ gravity and the buoyant force will exert a torque about the pivot point. The direction of the torque determines if we have a restoring force and a stable equilibrium. 
• Details of the calculation:
   

   

  

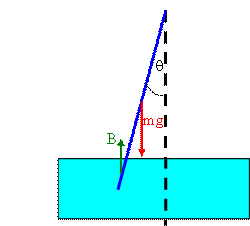
  Let the rod have length L and cross sectional area A (√A << L), and let aL be the length of the section of the rod in the water.  Assume the rod is displaced by a small angle θ.  In the small angle approximation, the torque about the pivot point is
  τ = mgLθ/2 - B(1 - a/2)Lθ = ½ρ_watergAL²θ/2 - ρ_watergaAL²(1 - a/2)θ, counterclockwise.
  As long as τ is positive we have a restoring force and a stable equilibrium.  When τ is negative we have an unstable equilibrium and the rod will deflect from the vertical.
  At the moment the rod begins to deflect from the vertical τ = 0.
  ½ρ_watergAL²θ/2 - ρ_watergaAL²(1 - a/2)θ = 0,  ½ - a(2 - a) = 0, a² - 2a + ½  = 0,
  a = (1 - √½).
  When the fraction of the rod under water is (1 - √½) ≈ 0.3, the rod begins to deflect from the vertical.