Error analysis and math

Problem:

An experimentalist makes independent measurements of the length and height of a rectangular feature.  The values and their standard deviations are 10.62 ± 0.46 microns and 12.46 ± 0.52 microns.  Calculate the perimeter P and the area A of the feature including the standard deviation of each.

Solution:

• Concepts:
  Propagation of errors
• Reasoning:
  We are asked to propagate experimental errors.
• Details of the calculation:
  P = 2 * (10.62 + 12.46) ± 2 * (0.46² +0.52²) ^½
  = 46.16 ± 1.39 microns
  (In addition and subtraction, the sum or the difference cannot be stated to more places after the decimal than the term with the least number of places after the decimal.)
  A = 10.62 * 12.46 ± ((0.46/10.62)² + (0.52/12.46)²) ^½ * 10.62 * 12.46
  = 132.33 ± 7.96
  = 132.3 ± 8.0 square microns
  (When numbers are multiplied or divided, the number of significant figures in the product or quotient cannot exceed that of the least precise number used in the calculation.)
  More rules:
  When using logarithms, the significant figures are those in the mantissa (the figures after the decimal); the characteristic (figure before the decimal) indicates the placement of the decimal in the original number: e.g. log(2731) = 3.4363.

Problem:

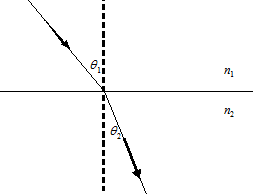
Propagation of Errors:  Snell's law relates the angle of refraction θ₂ of a light ray travelling in a medium of index of refraction n₂ to the angle of incidence θ₁ of a ray travelling in a medium of index n₁, as shown in the figure. 

From the knowledge that n₁ = 1.000 and from independent experimental measurements of
θ₁ = (22.03 ± 0.8)^o, and θ₂ = (10.45 ± 0.8)^o, find
(a) n₂ ;
(b) the percentage errors in sinθ₁ and in sinθ₂;
(c) the uncertainty in n₂.

Solution:

• Concepts:
  Propagation of errors
• Reasoning:
  We are asked to propagate experimental errors.
• Details of the calculation:
  (a)  sinθ₁ = n₂sinθ₂,  n₂ = sinθ₁/sinθ₂ = 2.07
  (b) d(sinθ)/sinθ = cotθdθ
  percentage error sinθ₁:  3.5%
  percentage error sinθ₂:  7.6%
  (c)  Δn₂ = n₂*((Δ(sinθ₁)/sinθ₁)² + (Δ(sinθ₂)/sinθ₂)²)^½ = 0.17

Problem:

A force F is applied on a square plate of side L.  If the percentage error (standard deviation) in determination of L is 3% and that in F is 4%, what is the error in pressure?

Solution:

• Concepts:
  Error propagation for uncorrelated variables
• Reasoning:
  We are asked to propagate the error in a set of measurements.
• Details of the calculation:
  Pressure P = F/A = F/L².
  (∆P/P)² = (∆F/F)² + (∆L²/L²)² = (∆F/F)² + (2∆L/L)² = 0.04² + 0.03² = 0.0025
  ∆P/P = 0.05.  The error in the pressure is 5%.

Problem:

Suppose C is the capture rate of dark matter in an astrophysical body.  Let C_A be the dark matter annihilation rate per effective volume.  Then an approximate Boltzmann equation governing the number N of dark matter particles in the astrophysical body is
dN/dt = C - C_AN².
If N(0) = 0, find N(t).
Hint:  ∫du/(1 - u²) = tanh^-1u

Solution:

• Concepts:
  Solving a differential equation
• Reasoning:
  The rate equation is given.
• Details of the calculation:
  dN/(C - C_AN²) = dt.  ∫₀^N dN'/(C - C_AN'²) = ∫₀^t dt' = t.  Let y = (C_A/C)^½N.
  (CC_A)^-½ ∫₀^y du/(1 - u²) = (CC_A)^-½ tanh^-1((C_A/C)^½N) = t
  (C/C_A)^½tanh((C_AC)^½t) = N(t)
  When t >> (CC_A)^-½ then N(t) --> (C/C_A)^½

Problem:

In a physics lab you are counting the number of gamma-rays resulting from the decay Cesium-137 with a Geiger tube.  You make about 10⁴ measurements in 0.2 s increments.  Cs-137 disintegrates with a probability of 6.5% directly and with a probability of 93.5% indirectly over the meta-stable barium-137m into stable barium-137.  During the indirect decay, beta rays having a maximum energy of 0.513 MeV are released.  The meta-stable Ba-137 changes into stable Ba-137 with a half-life of 2.55 minutes releasing a 0.662 MeV gamma ray.  The activity the Cs-137 is is deduced from the gamma rays.
The cesium source contains a very large number of ¹³⁷C_S atoms, but the probability that any atom decays in a 0.2 s time interval is small.  You adjust the relative position of the source and the detector, so that the average number of counts in a 0.2 s time interval is around 10.
(a)  Radioactive decay is a random event.  The Poisson distribution gives the probability of recording a particular number k of events in a 0.2 s time interval.  If λ is the average number of events in a 0.2 s time interval, what is the expression for Poisson distribution P(k).
(b)  For discrete random variables x we define the variance as  s² = ∑_xP(x)(x - <x>)², where P(x) is the probability of recording x, ∑_xP(x) = 1.
Show that this can be re-written as s² = <x²> - <x>².
(c)  Derive the variance and standard deviation of the Poisson distribution.

Solution:

• Concepts:
  The Poisson distribution
• Reasoning:
  For a large number of rare events  the probability of recording a particular number k of events is given by the Poisson distribution.
• Details of the calculation:
  (a)  P(k) = (λ^k/k!)e^-λ is the expression for Poisson distribution P(k).
  (b)   s² = ∑_xP(x)(x - <x>)² = ∑_xP(x)x² + ∑_xP(x)<x> -  2∑_xP(x)x <x>
  = <x>² + <x>∑_xP(x) + <x>∑_xP(x)x = <x>² + <x> - 2<x><x>
  = <x²> - <x>².
  (c)  s² = <k²> - <k>² = ∑_k≥0P(k)k² - (∑_k≥0P(k)k)².
  ∑_k≥0P(k)k² = ∑_k≥0(k²λ^k/k!)e^-λ = λe^-λ∑_k≥1(λ^k-1k/(k-1)!)
  = λe^-λ[∑_k≥1(λ^k-1(k-1)/(k-1)!) + ∑_k≥1(λ^k-1/(k-1)!)]
  = λe^-λ[λ∑_k≥2(λ^k-2/(k-2)!) + ∑_k≥1(λ^k-1/(k-1)!)]
  = λe^-λ[λ∑_i≥0(λⁱ/i!) + ∑_j≥0(λ^j/j!)]
  = λe^-λ[λe^λ + e^λ] =  λ[λ + 1] = λ² + λ.
  (∑_k≥0P(k)k)² = λ²,  s² = λ.
  The standard deviation of the Poisson distribution P(k) = (λ^k/k!)e^-λ is √λ.