The ideal gas law

Problem:

A tank having a volume of 0.1 m³ contains helium gas at 150 atm.  How many balloons can the tank blow up, if each filled balloon is a sphere 0.3 m in diameter at an absolute pressure of 1.2 atm?

Solution:

• Concepts:
  The ideal gas law, (Boyle's law)
• Reasoning:
  At constant temperature P₁V₁ = P₂V₂. (Boyle's law)
  We are given P₁, V₁, and P₂ and are asked to solve for V₂.
• Details of the calculation:
  P₁ = 150 atm = 1.515*10⁷ Pa. V₁ = 0.1m³.
  P₂ = 1.2 atm = 1.212*10⁵ Pa.
  V₂ = P₁V₁/P₂ = 12.5 m³.
  Let n = number of balloons and V_b = the volume of each blown-up balloon.
  V_b = (4π/3)r³ = 1.414*10^-2 m³.
  n = V₂/V_b = 884.  The tank can blow up 884 balloons.

Problem:

A vertical open glass tube of length h is half-submerged in mercury.  The top end of the tube is then closed and the tube is slowly pulled out until the bottom of the tube is barely submerged in the mercury.  What is the length of the mercury column remaining in the tube?  The atmospheric pressure corresponds to the pressure of a column of mercury of height H.  Assume the temperature is constant.

Solution:

• Concepts:
  The ideal gas law
• Reasoning:
  At constant temperature  PV = constant (Boyle's law).
  When a length h/2 of the tube is above the mercury, the volume of the gas in the tube is Ah/2 and the pressure is atmospheric pressure P₀.
  When a length h of the tube is above the mercury, the mercury rises to a height h₁ and the gas occupies a volume A(h - h₁).  Since PV = constant (Boyle's law), the gas pressure is
  P = ½P₀h/(h-h₁).
  We have P₀ = ½P₀h/(h-h₁) + ρ_mercurygh₁.
• Details of the calculation:
  Given: ρ_mercurygH = P₀, so P₀ = ½P₀h/(h-h₁) + P₀h₁/H. 
  Therefore
  ½hH = h₁H + h₁h - h₁²,  h₁² - h₁(H + h) + ½hH = 0,  h₁ = (H + h)/2 - (H² + h²)^½/2,

Problem:

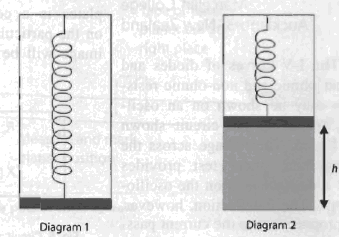
A movable heavy piston is supported by a spring inside a vertical cylindrical container as shown.  When all air is pumped out of the container, the piston is in equilibrium, as shown in diagram 1, with only a tiny gap between the piston and the bottom of the container.  When a portion of gas at temperature T is introduced under the piston, the piston rises to a height h as shown in diagram 2.

What would be the height of the piston above the bottom of the container if the gas was heated to temperature 2T?  Assume the piston moves without friction and that the spring obeys Hooke's law. 

Solution:

• Concepts:
  The ideal gas law, Hooke's law
• Reasoning:
  Let k be the spring constant of the spring.  In equilibrium PA = kh.
  P = pressure, A = area of piston, h = height of the piston above the bottom
• Details of the calculation:
  P₁/P₂ = h₁/h₂.  (Hooke's law)
  From the ideal gas law we have P₁V₁/T₁ = P₂V₂/T₂.
  Here T is the absolute temperature.
  V = hA, so P₁h₁/T₁ = P₂h₂/T₂,
  With T₂ = 2T₁ we have P₂ = 2P₁h₁/h₂,  (h₁/h₂)² = ½.
  So if the piton rises to a height h when the gas temperature is T,
  then it rises to height (√2)h when the gas temperature is 2T.

Problem:

Near the surface of Earth where the gravitational acceleration has magnitude g, derive an expression for the atmospheric pressure as a function of altitude y assuming that
(a)  the temperature T is constant.
(b)  the temperature T is not constant, it decreases with altitude y.  In the standard atmosphere T = T₀ - ay, with a = 0.0065 K/m.
Assume the atmosphere is an ideal gas of molecules with particle mass m.

Solution:

• Concepts:
  The ideal gas law
• Reasoning:
  Let us consider a column of gas containing ρ_particle particles of mass m per unit volume near the Earth's surface. 

  

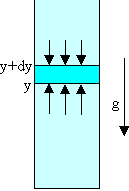
  The pressure times the area (i.e.  the force) at height y must exceed that at height y + dy by the weight of the intervening gas.
  We need P_y+dyA - P_yA = -mρ_particleVg = -mρ_particlegAdy,  or dP = -mρ_particlegdy.
  The ideal gas law lets us express ρ_particle in terms of the temperature and the pressure.

• Details of the calculation:
  (a)  T is constant.
  From the ideal gas law we know that P = ρ_particlekT, with k being the Boltzmann constant.  We may therefore write
  dP = -P(mg/kT)dy, or dP/P = -(mg/kT)dy. 
  This integrates to 
  P = P₀e^-mgy/(kT). 
  The pressure decreases exponentially with altitude.
  (b) T = T₀ - ay.  We now have 
  dP/P = -mgdy/(k(T₀ - ay)). 
  This integrates to 
  ln(P/P₀) =( mg/ka)ln(1 - ay/T₀), or 
  (P/P₀)^(ka/mg) = (1 - ay/T₀).

Problem:

(a)  By considering the forces acting on a thin concentric shell of atmosphere at a distance r from the center of the earth, show that the variation of pressure P with height in terms of the local density of the atmosphere ρ and the local gravitational acceleration g is given by 

dP/dr = -ρg.

(b) If the temperature is 27^o C at the earth's surface and the atmosphere is assumed to be an ideal gas composed approximately of 80% diatomic ¹⁴N and 20% diatomic ¹⁶O, estimate the vertical distance over which the pressure falls to 1/e of its value at the surface (this is called the scale height of the atmosphere).  To simplify your estimate you may assume the temperature to remain constant with height above the surface (which typically introduces an error of ~20% compared to a more realistic variation of temperature).

Solution:

• Concepts:
  Pressure, the ideal gas law
• Reasoning:
  Consider a volume of air of height h in equilibrium.  It does not rise or fall.  The net force on it must be zero. 
  Therefore P_bottom - P_top = ρhg.  The ideal gas law relates the density to the pressure.
• Details of the calculation:
  (a) Since R_Earth >> h, the height of the atmosphere, we may consider the concentric shells locally flat.  Then
  F_net = P_bottomA - P_topA - ρAΔrg = 0.
  P_top - P_bottom = -ρΔrg.
  dP/dr = -ρg.
  (b)  dP/dr = -(0.2 m_O + 0.8 m_N)ρ_particleg = -mρ_particleg.
  m = 0.2*32u + 0.8*28u = 28.8u = 4.784*10^-26 kg.
  But from the ideal gas law we know that P = ρ_particlekT, with k being the Boltzmann constant.  We may therefore write
  dP/dr = -P(mg/kT), or 
  dP/P = -(mg/kT)dr.
  If the temperature T is constant, then this integrates to 
  P = P₀exp(-mg(r-r₀)/(kT)).
  For P/P₀ = 1/e we need mg(r-r₀)/(kT)  = 1,  r - r₀ = kT/mg.
  kT = 1.381*10^-23*300 J.  r - r₀ = 8.84 km.
  This is much less than R_Earth = 6.37*10³ km, so the locally flat assumption is justified.

Problem:

Consider a circular cylinder of radius R and length L, rotating about its symmetry axis with angular velocity ω and containing an ideal gas with particles of mass M.  We assume that the system is in thermal equilibrium at temperature T = 300 K, that the gas is at rest in a reference frame rotating with the cylinder, and that the particle velocities are small enough that we can ignore all the Coriolis forces.  
(a)  If P(0) is the pressure on the axis of rotation, find the pressure P(r) between r = 0 and r = R.
(b)  If R = 1 km, the gas consists of Nitrogen molecules, ω = 0.2/s, and P(R) = 101 kPa, find the pressure on the axis.
(c)  If R = 0.1 m, the gas consists of Nitrogen molecules, ω = 0.2/s, and P(R) = 101 kPa, find the pressure on the axis.

Solution:

• Concepts:
  Fictitious forces in an accelerating frame
• Reasoning:
  Fictitious forces appear in the rotating frame.  Consider the gas in a cylindrical shell of radius r and thickness dr.  The centrifugal outward force on the gas must be balanced by a force due to a pressure difference. 
• Details of the calculation:
  (a)  (P_out - P_in)2πr  = ρ2πr dr ω²r
  dP/dr = (N/V)Mω²r
  Ideal gas law:  P = (N/V)kT
  Therefore dP/dr = (P/(kT))Mω²r,  dP/P = Mω²rdr/(kT).
  Integrating we obtain P(r) =  P(0)exp(Mω²r²/(2kT)).
  (b)  M/(2kT) = 28*1.66*10^-27/(2*1.38*10^-23*300) = 5.61*10^-6.
  ω²r² = 4*10⁴.
  exp(Mω²r²/(2kT)) = 1.25
  P(0) = 101kPa/1.25 = 81 kPa.
  (c)  ω²r² = 4*10^-4.
  exp(Mω²r²/(2kT)) = 2.2*10^-9
  P(0) ≈ P(R).