Radiation laws

Problem:

The Proton-Proton Chain is the principal set of reactions for solar-type stars to transform hydrogen to helium:
¹H + ¹H --> ²H + e⁺ + neutrino
Two protons react to form deuterium plus a positron and a neutrino
²H + ¹H --> ³He + gamma-ray
The deuterium reacts with another proton to form ³He  plus another gamma-ray. 
³He + ³He --> ⁴He + 2 ¹H
Two ³He nuclei react to form ⁴He and two protons.
Each proton-proton cycle generates 26.7 MeV of energy.  The Sun emits approximately 4*10²⁶ Watts of energy.  Calculate the rate at which the sun generates neutrinos and estimate the number of solar neutrinos aping through Earth each second. Assume the sun's energy production is entirely by the proton-proton cycle.

Earth-Sun distance:  1.5*10^-11 m
Earth radius:  6.37*10⁶ m

Solution:

• Concepts:
  Nuclear fusion, the 1/r² law for flux of conserved quantities
• Reasoning:
  Each proton cycle generates 26.7 J MeV = 4.27*10^-12 J
  (4*10²⁶ J/s)/( 4.27*10^-12 J/proton cycle) = 9.36*10³⁷ proton cycles per second
  There are two neutrinos produced in each proton cycle, so ~2*10³⁸ neutrinos are produced per second.
• Details of the calculation:
  Assuming isotropic emission, the neutrino flux at a distance of R = 1.5*10^-11 m is
  F = 2*10³⁸/(4πR²) = 7*10¹⁴/(m²s)
  Multiplying by the cross-sectional area of Earth, we estimate ~9*10²⁸ neutrinos passing through Earth each second.

Problem:

Most of the neutrinos from the Sun are produced in the chain of processes called the "pp-cycle":
(1)   p + p --> ²H + β⁺ + ν
(2)   p + ²H --> ³He + γ
(3)  ³He + ³He --> ⁴He + p + p
Estimate the order of magnitude of the neutrino flux (neutrinos/(cm²s) from these reactions on Earth using the following data:
Earth-Sun distance = 1.5*10¹¹ m
proton mass = 938.272 MeV/c^2
4He mass = 3727.379 MeV/c²
Assume the Earth can be modeled as a black body with temperature T = 300 K.  On average, it emits as much radiation as it receives from the Sun.  Use this to estimate the energy flux from the sun on Earth.

Solution:

• Concepts:
  Nuclear energy, radiation laws
• Reasoning:
  Producing one ⁴He nucleus releases 2 neutrinos.  If we find the amount of energy released in the production of one ⁴He, we can relate the neutrino flux to the energy flux.
• Details of the calculation:
  E = 4m(p)c² - m(⁴He)c² = 25.7 MeV.
  The positrons will annihilate with electrons, thus producing gammas (energy).
  Thus 2 neutrinos are produced for every 25.7 MeV of energy that is released.

  What is the solar energy flux at the sun-earth distance?
  We assume that it is equal to the power per unit area emitted by Earth.
  I = σT⁴ =   (5.67 * 10^-8 W m^-2 K^-4)*(300 K)⁴ = 459 W/m² = 2.87*10¹⁵ MeV/(m²s).
  We therefore expect a neutrino flux of approximately 2* 2.87*10¹⁵ /25.7 neutrinos/(m²s),
  or 2.23*10¹⁴ neutrinos/(m²s) = 2.23*10¹⁰ neutrinos/(cm²s).
  (The energy flux is underestimated, the real neutrino flux is ~6*10¹⁰ neutrinos/(cm²s).)

The Wien law and the Stefan-Boltzmann law

Problem:

The light from the sun is found to have a maximum intensity near 470 nm.  Assuming the surface of the sun behaves as a black body, calculate the temperature of the sun.

Solution:

• Concepts:
  The Wien law
• Reasoning:
  λ_max(nm)= 3*10⁶/T(K). 
• Details of the calculation:
  T = (3*10⁶/470) K = 6383 K

Problem:

An ideal radiator radiates with a total intensity of I = 5.68 kW/m².  At what wavelength does the spectral emittance I(λ) peak?
(Give a numerical answer!)

Solution:

• Concepts:
  The Stefan Boltzmann law, the Wien displacement law
• Reasoning:
  The Stefan Boltzmann law:  I = σT⁴, σ is the Stefan-Boltzmann constant.
  The Wien displacement law:  λ_max =  σ_w /T,  σ_w is the Wien displacement law constant.
  Given I, we find T and given T we find λ_max.
• Details of the calculation:
  Here T⁴ = (5680 W m^-2)/( 5.67 * 10^-8 W m^-2 K^-4),  T = 563 K.
  λ_max =  (2.898 * 10^-3 m K)/(563) = 5.15 * 10^-6 m = 5.15 μm.

Problem:

Two concentric long tubes have radii R₁ = 5 cm and R₂ = 6 cm.  The outer tube is maintained at temperature T₂ = 300 K and the inner tube at temperature T₁ = 4 K.  Find the net thermal power absorbed by a 10 cm length of the inner tube, assuming that the emissivity is unity for both surfaces.

Solution:

• Concepts:
  Radiation heat transfer between black surfaces, the Stefan-Boltzmann law
• Reasoning:
  The energy radiated by a blackbody per second per area is proportional to the fourth power of the absolute temperature, P/A = σT⁴.
  A Blackbody absorbs all incident radiation.
• Details of the calculation:
  Assume the tubes are infinitely long all the energy radiated by one tube is absorbed by the other tube.
  Power radiated by inner tube per length L:  P₁ = 2πR₁LσT₁⁴.
  Power radiated by outer tube per length L:  P₂ = 2πR₂LσT₂⁴.
  Net thermal power absorbed by a 10 cm length of the inner tube:
  P₂ - P₁ = 2πσL (R₂T₂⁴ - R₂T₂⁴) = 17.31 W.

Problem:

Estimate the temperature of the surface of Earth if the flux of solar energy at the Sun-Earth distance is ~1360 W/m²  and ~30% of solar energy is reflected back by the atmosphere.  (Make reasonable assumptions and justify them.)

Solution:

• Concepts:
  The Stefan-Boltzmann Law
  Radiated power = emissivity * σ * T⁴ * Area, σ = 5.67*10^-8W/(m²K⁴)
• Reasoning:
  In steady state Earth's surface must radiate as much energy as it absorbs per second.
• Details of the calculation:
  Assume (0.7*1360 W/m²)πR²  reaches the surface of Earth.
  If the emissivity is not a function of wavelength (temperature) then
  (0.7*1360 W/m²)πR²  = 0.7*(5.67*10^-8W/(m²K⁴))*T⁴*4πR²,  T = 278 K.
  This is probably too cold.  The emissivity of the surface and/or atmosphere must be a function of wavelength (greenhouse effect).

Problem:

A black plane surface at a constant high temperature T_h is parallel to another black plane surface at a constant lower temperature T_l.  Between the plates is vacuum.
In order to reduce the heat flow due to radiation, a heat shield consisting of two thin black plates, thermally isolated from each other, is placed between the warm and the cold surfaces and parallel to these.  After some time stationary conditions are obtained.  By what factor X is the stationary heat flow reduced due to the presence of the heat shield?  Neglect end effects due to the finite size of the surfaces.

Solution:

• Concepts:
  Equilibrium, radiation heat transfer, the Stefan-Boltzmann law
• Reasoning:
  The energy radiated by a blackbody per second per unit area is proportional to the fourth power of the absolute temperature, P/A = σT⁴.
  Under stationary conditions the net heat flow is the same everywhere:
• Details of the calculation:
  
  
  Combining these three equations we get 3J = σ(T_h⁴ - T_l⁴) = J₀, where J₀ is the heat flow in the absence of the heat shield. Thus X = J/J₀ takes the value X = (1/3).

Problem:

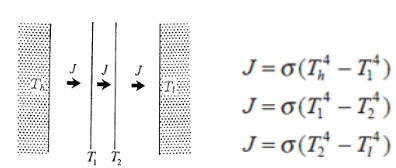
A sphere of radius 3 cm acts like a blackbody.  It is equilibrium with its surroundings and absorbs 30 kW of power radiated to it from the surroundings.  What is the temperature of the sphere?

Solution:

• Concepts:
  The Stefan-Boltzmann law
• Reasoning:
  The power absorbed by a blackbody is P_a = σAT_a⁴.
• Details of the calculation:
  (30*10³ W) = (5.67*10^-8 (W/m²) K⁴) 4π(0.03 m)² T_a⁴.
  T_a⁴ = 4.68*10¹³.
  T_a = temperature of surroundings = 2600 K.  Since the body is in equilibrium with its surroundings, it is at the same temperature, 2600 K.

Problem:

The rate at which the radiant energy reaches the surface of earth from the sun is about 1.4 kW/m².
The distance from earth to the sun is about 1.5 * 10¹¹ m, and the radius of sun is about 0.7 * 10⁹ m.
(a)  What is the rate of radiation of energy, per unit area, from the sun's surface?
(b)  If the sun radiates as an ideal black body, what is the temperature of its surface?

Solution:

• Concepts:
  The Stefan-Boltzmann law
• Reasoning:
  The power radiated by a blackbody is P = σAT⁴.
• Details of the calculation:
  (a)  Let D = distance from the sun to the earth
  Let P = energy radiated from the surface of the sun per second.
  Every one second, P joules of energy are radiated from the surface of the sun and this energy passes through the surface of a sphere of radius D centered at the sun.
  The energy passing through a unit area per second = P/4πD² = 1.4 * 10³ Wm^-2.
  Therefore P = 4π(1.5 * 10¹¹)² * (1.4 * 10³) W = 3.96 * 10²⁶ W.
  I = (3.96 * 10²⁶ W)/(4π (0.7 * 10⁹)²) = 6.43 * 10⁷ W/m² = rate of radiation of energy, per unit area, from the sun's surface.
  (b)  If the sun is an ideal black body with emissivity 1 then  I = σT⁴, 
  T = (6.43 * 10⁷/5.67 * 10^-8)^1/4 K = 5803 K.

Problem:

In very massive stars the pressure from electromagnetic radiation can greatly exceed that from the gas.
(a)  Show that in the hot interior of a star the radiation pressure is P_rad = aT⁴/3, where
a = 4σ/c and σ is the Stefan Boltzmann.
(b)  Assuming a spherical star described by classical Newtonian gravity and a classical electromagnetic field, find an expression for the temperature gradient at the surface of a star when the force per unit volume associated with the radiation pressure is exactly balanced by the force per unit volume associated with gravity, assuming that the gas pressure can be neglected.
(c)  For stars dominated by radiation the temperature gradient is known to take the form
dT/dr = -3ρkL/ (16π a c T³r²),
where T is temperature, L = L(r) is the luminosity (energy per unit time crossing the radius r), and k is a measure of how strongly the photons interact with matter (opacity).  Use this and the first result to show that the star is unstable against radiation blowing surface layers off the star if the luminosity exceeds L = 4πcGM/k, where k is evaluated at the surface.
Hint:  You can complete parts (b) and (c) without completing part (a) by using the result given in part (a).

Solution:

• Concepts:
  Stefan-Boltzmann law, equilibrium
• Reasoning:
  The Stefan-Boltzmann law gives the power radiated by a blackbody as a function of temperature.  We need to relate the power to the radiation pressure.
• Details of the calculation:
  (a)  Consider the hot interior of a star to be a blackbody.  The Stefan-Boltzmann Law gives the total energy being emitted at all wavelengths by a blackbody.
  Radiated power = σ*T⁴*Area.
  Consider an area dA and the photon energy in a ring at a distance between r and r + dr from dA.

  

   

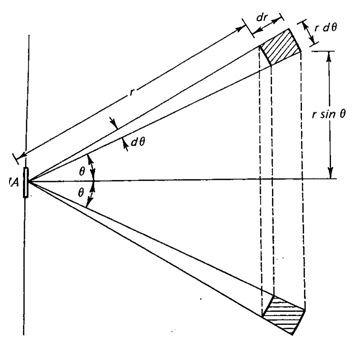
  The probability that this energy will reach the area dA is dA cosθ/(4πr²). 
  Denote the photon energy density in the ring by u.
  The amount of energy E reaching dA from the ring is
  u2πr²sinθ dr dθ dA cosθ/(4πr²) = u sinθ dr dθ dA cosθ/2.
  The total energy reaching dA in a time interval dt comes from rings with radii between r = 0 and r = cdt.  It is therefore given by
  I dA dt = ∫₀^π/2 dθ u dA cdt sinθ cosθ/2 = ¼ u dA cdt.
  I = ¼ u c.

  Setting (u c)/4 = σ*T⁴, we find the energy density in the volume u = (4σ/c)*T⁴. 
  The pressure exerted by a photon gas is P = u/3. 
  So P_rad in the interior of the star is (4σ/(3c))*T⁴ = (a/3) T⁴.
  (For any gas: PV = N<p·v>/3.  For a photon p = E/c and v = c, so p·v = E.
  N<E> = U = internal energy of the photon gas, P = U/(3V) = u/3.)
  (b)  Consider a thin spherical shell of radius r and mass dm = ρ4πr²dr inside the star.  The gravitational force per unit area on this layer is is Gm_inside ρdr/r², pointing towards the center of the star.  In equilibrium, P_top + Gm_inside ρdr/r² = P_bottom.
  dP/dr = -Gm ρ/r² near the surface of the star.  If the star is supported by radiation pressure P_rad = aT⁴/3, then we need dP_rad/dr = (4/3)aT³(dT/dr) = -Gm ρ/r².
  We need dT/dr = -3Gm ρ/(4aT³r²).
  (c)  Let dT/dr = -3ρkL/ (16π ac T³r²) = -3Gm ρ/(4aT³r²), i. e. let the star be in equilibrium. 
  Then L = 4πcGm/k.
  If L exceeds this value the surface layer of the star experiences a net outward force.

Problem:

The Sun's spectrum, I(hν), peaks at 1.4 eV, the spectrum of Sirius A peaks at 2.4 eV, and the luminosity (total amount of energy radiated per unit time) of Sirius A is 24 times larger than that of the Sun.  Compute the diameter of Sirius A in units of the Sun's diameter.

Solution:

• Concepts:
  Stefan-Boltzmann constant:  Radiated power = σ * T⁴ * Area.
  Wien law:  ν_max = constant *T
• Reasoning:
  The Wien law yields the temperature of the star.  The energy radiated by a blackbody per second per area is proportional to the fourth power of the absolute temperature, P/A = σT⁴.
  Details of the calculation:
  diameter D ∝ √A ∝ √L/T²,  D₁/D₂ = √(L₁/L₂)*(T₂/T₁)².  L = luminosity.
  T_Sun/T_{Sirius A} = 1.4/2.4 = 0.583
  L_{Sirius A} /L_Sun = (T_{Sirius A}⁴ D_{Sirius A}²)/(T_Sun⁴ D_Sun²) = 24
  D_{Sirius A}/D_Sun = √(24)* (T_Sun/ T_{Sirius A})² = 1.67

Problem:

Sirius A is the brightest star in the night sky, with the peak of its spectral emittance at a wavelength of 291 nanometers.
(a)  If one makes the reasonable assumption that the star radiates as a blackbody, what is its effective temperature? 
(b)  If the flux measured on Earth from Sirius A is 1.17 * 10^-7 W/m², and the distance is known to be 8.6 light-year, what is the radius of Sirius A?

Solution:

• Concepts:
  The Wien law, the Stefan-Boltzmann law, energy conservation
• Reasoning:
  Wien displacement law constant:  σ_w = 2.897 7685 * 10^-3 m K
  Stefan-Boltzmann constant:  σ =   5.670 400 * 10^-8 W m^-2 K^-4
  T = σ_w /λ_max.  Radiated power = σ*T⁴*A.
• Details of the calculation:
  (a)  T = 10⁴ K is the effective temperature.
  (b)  Radiated power per unit area: M = σ*T⁴ = 5.67*10⁸ W/m²
  Total power:  P = M*4πR²,  R = radius of Sirius
  Flux at distance d: E = P/(4πd²) = MR²/d², 
  R² = (8.6* 9.46*10¹⁵ m)²*(1.17 * 10^-7 W/m²)/ (5.67*10⁸ W/m²)
  R = 1.2*10⁹ m.

Planck's law

Problem:

Inside a blackbody cavity, the energy density per unit frequency interval, ρ(ν), is given by Planck's formula

ρ(ν) = (8πν²/c³)hν/(exp(hν/(kT)) - 1).

(a)  Derive an expression for the intensity per unit frequency interval, I(ν), of the radiation emitted by the blackbody.
(b)  Derive the Stefan-Boltzmann law.
(c)  Derive Wien's displacement law.

∫₀^∞x³dx/(e^x - 1) = π⁴/15.

Solution:

• Concepts:
  Blackbody radiation
  Reasoning:
  We are asked to derive the  Stefan-Boltzmann law and the Wien law.
  Experimental realization of a black body:
  Use the inside of a large box (oven) held at a constant temperature T. A small hole is cut in one side. Any radiation that enters through the hole bounces around inside and has little chance of ever getting out again. Eventually it gets absorbed. Radiation coming out the hole is as good a representation of the radiation from a perfect emitter.
  How do you calculate the intensity of the radiation coming out of the small hole?
• Details of the calculation:
  (a)  Consider an area dA and the energy per unit frequency interval in a ring at a distance between r and r + dr from dA.
  

  The probability that this energy will reach the area dA is dA cosθ/(4πr²). 
  The amount of energy per unit frequency interval reaching dA from the ring is
  ρ(ν)2πr²sinθ dr dθ dA cosθ/(4πr²) = ρ(ν)sinθ dr dθ dA cosθ/2.
  The total energy per unit frequency interval reaching dA in a time interval dt comes from rings with radii between r = 0 and r = cdt.  It is therefore given by
  I(ν) dA dt = ∫₀^π/2 dθ ρ(ν) dA cdt sinθ cosθ/2 = ¼ ρ(ν) dA cdt.
  I(ν) = ¼ ρ(ν) c.
  
  (b)  To find the total intensity, integrate over all frequencies.
  ∫₀^∞(2π/c²)hν³ dν/(exp(hν/(kT)) - 1) = (2πk⁴T⁴/(h³c²))∫₀^∞ x³ dx/(exp(x) - 1)
  = (2πk⁴T⁴/(h³c²) π⁴/15 = (2π⁵k⁴T⁴/(15h³c²) = σT⁴.
  Here σ is the Stefan-Boltzmann constant.

  (c)  The Wien Law gives the wavelength of the peak of the radiation distribution.
  |I(ν)dν| = |I(λ)dλ|,  I(λ) = I(ν)|dν/dλ| = (c/λ²)I(ν).
  I(λ,T) = [2hc²/λ⁵][1/(exp(hc/(λkT)) - 1)].

  dI(λ)/dλ = 0 --> (d/dλ)(λ⁵(exp(hc/λkT - 1))^-1 = 0.
  [hc/(λkT)][[exp(hc/(λkT))/(exp(hc/(λkT)) - 1)²] - 5 = 0,
  xe^x/(e^x - 1) - 5 = 0.

  Use a calculator to find x ~ 4.96.
  λ_max = hc/(xkT)  ~ (2.9*10^-3 mK/T).

Problem:

Inside a blackbody cavity, the energy density per unit frequency interval, ρ(ν), is given by Planck's formula
ρ(ν) = (8πν²/c³) hν/(exp(hν/kT) - 1).
The intensity per unit frequency interval, I(ν), of the radiation emitted by the blackbody is given by I(ν) = ¼ ρ(ν) c.
Commonly, Wien's displacement law is written as λ_max (m) = (2.9*10^-3 m K)/T.
Derive the Wien's displacement law for the frequency ν_max (s^-1), and show that ν_max is NOT equal to c/ λ_max.  Why?

Solution:

• Concepts:
  Blackbody radiation
• Reasoning:
  We are asked to derive the Wien law in terms of frequency.
• Details of the calculation:
  The Wien Law in terms of frequency gives the frequency of the peak of the radiation distribution.
  dI(ν)/dν = 0.
  I(ν) = (2πh/c²) (ν³/(exp(hν/kT) - 1)).
  d(ν³/(exp(hν/kT) - 1))/dν = 0.
  Let x =  hν/kT.
  d(x³/(exp(x) - 1))/dx = 0.
  xe^x/(e^x - 1) = 3.
  Use a calculator to find x ~ 2.82. 
  ν_max = (5.88*10¹⁰ Hz/K) T(K),  ν_max is proportional to the absolute temperature T.
  c/λ_max = (3*10⁸ m/s)*T/(2.898* 10^-3 m K). 
  c/λ_max = ~(1*10¹¹ Hz/K) T(K),  ν_max is NOT equal to c/λ_max.
  This is because  I(λ) is not equal to I(ν).
  |I(ν)dν| = |I(λ)dλ|,  I(λ) = I(ν)|dν/dλ| = (c/λ²)I(ν).