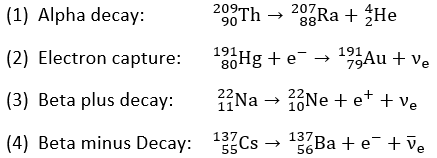The Bohr atom, nuclear decay

Bohr atom

Problem:

Consider a Bohr-type, classical model of a hydrogenic atom, where a structureless electron with charge -q_e is orbiting a (stationary) structureless nucleus with charge Zq_e in a circular orbit in the xy-plane without radiating.  Let the angular momentum vector of the electron be L = Lk and have magnitude L = nħ.
(a)  What is the orbital radius r₀ of the electron?
(b)  What is the kinetic energy of the electron and what is its total energy?
(c)  What is the magnetic dipole moment μ of the atom?

Solution:

• Concepts:
  The classical Bohr atom
• Reasoning:
  The Bohr atom introduces angular momentum quantization, but otherwise is a classical model.
• Details of the calculation:
  (a)  kZq_e²/r₀² = mv²/r₀,  mvr₀ = nħ,  r₀ =  n²ħ²/(mkZq_e²).  Let α = kZq_e².  r₀ = L²/(mα).
  (b)  ½mv² = ½α/r₀ = mα ²/(2n²ħ²).  E_total = T + U = -½α/r₀ = -m(kZq_e²)²/(2n²ħ²).
  (c)  μ = IA n = -(q_ev/(2πr))(πr²) n = = -½q_evr = -(q_e/(2m))L = -μ_Bn k.

Nuclei and particles

Problem:

Calculate the binding energy of the deuteron, which consists of a proton and a neutron, given that the mass of a deuteron is 2.013553 u.

Solution:

• Concepts:
  Nuclear binding energy
• Reasoning:
  The binding energy represents how much energy we would have to supply to pull the nucleus apart into separate free nucleons. 
• Details of the calculation:
  Binding energy: (m_p + m_n)c² - m_dc² = 2.2 MeV

Problem:

Calculate the disintegration energy Q for the beta decay ³²P --> ³²S + e^- + ν.
Atomic masses:  m(³²P) = 31.97391 u, m(³²S) = 31.97207 u

Solution:

• Concepts:
  Nuclear disintegration energy
• Reasoning:
  Atomic masses include the masses of the atomic electrons.  In β^- decay subtracting the atomic masses automatically takes into account the mass of the emitted electron. This is not true for β⁺ decay.  The mass of the neutrino is negligibly small.
• Details of the calculation:
  Q = m_ic² - m_fc². 
  m_i = m_nuc(³²P) = m(³²P) - 15*m(e^-),
  m_f = m_nuc(³²S) + m(e^-) = m(³²S) - 16*m(e^-) + m(e^-) = m(³²S) - 15*m(e^-)
  Q = m_ic² - m_fc² = (m(³²P) - m(³²S))c² = 1.71 MeV.

Problem:

Complete the decays by replacing 'X' (and 'A', 'Z','Y', where relevant), and state the name of the decay mode

Solution:

• Concepts:
  Nuclear decay modes
• Reasoning:
  

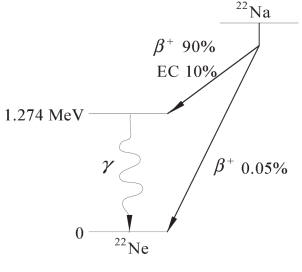
Aside:
10% of the time ²²Na decays via electron capture, which produce an excited state of ²²Ne, which then decays by emission of a 1.274 MeV gamma ray.

Problem:

Consider the case of a chain of two radioactive decays. Nucleus A decays into another B by one process, then B decays into another C by a second process, i.e. A → B → C.
The mean life of A is τ_A = 1/λ_A, and the mean life of B is τ_B = 1/λ_B,
Initially N_0A nuclei of type A are present and N_0B = 0.
(a)  Find the decay rate (the number of decays per second) for B in terms of  N_0A, λ_A, and λ_B,
(b)  Find approximate expressions for the decay rate if
(i)  λ_A >> λ_B,  (ii)  λ_A << λ_B,  (iii)  λ_A ≈ λ_B,

Solution:

• Concepts:
  Radioactive decay
• Reasoning:
  The decay of an unstable nucleus is a random (probabilistic) process.  The rate at which nuclei decay is proportional to the number N of nuclei present.
• Details of the calculation:
  (a)  dN_A/dt = - λ_AN_A,  N_A(t) = N_0Aexp(-λ_At).
  dN_B/dt = λ_AN_A - λ_BN_B.  (feed rate plus decay rate)
  dN_B/dt = λ_AN_0Aexp(-λ_At) - λ_BN_B.
  Try a solution N_B = C exp(-λ_At) + D exp(-λ_Bt).
  D = - C since N_B(0) = 0.
  N_B = C(exp(-λ_At) -  exp(-λ_Bt)),
  dN_B/dt = -C(λ_Aexp(-λ_At) -  λ_Bexp(-λ_Bt)) = λ_AN_0Aexp(-λ_At) - λ_BC(exp(-λ_At) -  exp(-λ_Bt)),
  -Cλ_A = λ_AN_0A - λ_BC,  C =  λ_AN_0A/(λ_B - λ_A).
  N_B(t) = [λ_AN_0A/(λ_B - λ_A)](exp(-λ_At) -  exp(-λ_Bt)).
  Decay rate: R_B = -λ_BN_B = -[λ_Bλ_AN_0A/(λ_B - λ_A)](exp(-λ_At) -  exp(-λ_Bt)).
  
  (b)  (i)  If λ_A >> λ_B,  R_B(t) ≈ -λ_BN_0Aexp(-λ_Bt).  The mean life of A is very short compared to the mean live of B, and nearly all A nuclei have decayed into B nuclei in a time interval very much smaller than τ_B.
  (ii)  λ_A << λ_B,  R_B(t) ≈ -λ_AN_0Aexp(-λ_At).  The mean life of A is very long compared to the mean live of B.  When a nucleus A decays, the nucleus B that was formed is likely to decay in a time interval very much smaller than τ_A.
  (iii)  λ_A ≈ λ_B, write λ_A = λ, λ_B ≈ λ + ε.
  R_B  ≈ -[λ²N_0A/ε](exp(-λt) (1 - 1 +  εt) = -λ²N_0At(exp(-λt).
  As ε --> 0 this becomes the exact solution  for λ_A = λ_B = λ.

Problem:

A 1 MeV neutron beam is incident on an boron (20% ¹⁰₅B + 80% ¹¹₅B) target of thickness 2 cm.  The density of the boron target is ρ = 2.3 g/cm³.  The total cross section σ_tot for interacting with the target (scattering plus attenuation) is 2.68 barns per atom for ¹⁰₅B and 2.13 barns per atom for ¹¹₅B.  Find the ratio of the transmitted flux to the incident flux, i.e. the attenuation of the neutron beam. 

Solution:

• Concepts:
  Cross section and attenuation coefficient
• Reasoning:
  F = F₀exp(-μx),  σ(cm²)*N(atoms/cm³) = μ = attenuation coefficient.
  (Assume the target is 20% ¹⁰₅B by weight.)
• Details of the calculation:
  μ = 0.2*(2.68 barns/atom)*(10^-24 cm²/barn)(6*10²³ atoms/mole)*(1 mole/10 g)*(2.3 g/cm³)
  + 0.8*(2.13 barns/atom)*(10^-24 cm²/barn)(6*10²³ atoms/mole)*(1 mole/11 g)*(2.3 g/cm³)
  = 0.288/cm.
  F = F₀exp(-0.288*2) = 0.56 F₀.

Problem:

The dominant interactions between nucleons in a nucleus are the short range nuclear force and the long-range electrostatic force.  Nucleons are only attracted by other nucleons in their neighborhood, but protons are repelled by all other protons in the nucleus.  When a large nucleus fissions, the net attractions between nucleons stays roughly the same, while the net repulsion decreases significantly.
To get a feeling for the amount of energy released in a fission reaction, calculate the electrostatic potential energy of two fragments, say a Cesium and a Zirconium nucleus when separated by a distance 2D₀, twice the range of the nuclear force. 
(D₀ is approximately 4 times the proton diameter, D₀ = 4*1.4*10^-15 m.)

Solution:

• Concepts:
  Electrostatic potential energy
• Reasoning:
  The electrostatic potential energy of two charges Q₁ and Q₂ separated by a distance r is  U = kQ₁Q₂/r, where k = 9*10⁹ Nm²/C².
• Details of the calculation:
  For Cesium Z = 55 and for Zirconium Z = 40.
  U = (9*10⁹ Nm²/C²)(55*40*(1.6*10^-19)² C²)/(2*4*1.4*10^-15 m) = 4.5*10^-11J = 282 MeV.