Eigenvalues and Boltzmann statistics

Problem:

Due to the presence everywhere of the cosmic background radiation the minimum possible temperature of a gas in interstellar space is 2.7 K.  This implies that a significant fraction of molecules in space may be in low-level excited states.  Consider a hypothetical molecule with one possible excited state.  What would the excitation energy have to be for 20% of the molecules to be in the excited state?

Solution:

• Concepts:
  Boltzmann statistics
• Reasoning:
  Boltzmann statistics tells us that N_excited/N_ground = e^-ΔE/kT, if the degeneracy of both states is 1. 
• Details of the calculation:
  0.2/0.8 = exp(-ΔE/(kT))
  ln(0.25) = -ΔE/(kT)
  ΔE = -ln(0.25)*(kT) = -ln(0.25)*8.617*10^-5*2.7 eV = 3.2*10^-4 eV = 0.32 meV

Problem:

Consider a particle in a simple two level system with eigenstates ψ₁ and ψ₂ such that
Hψ₁ = E₁ψ₁ and Hψ₂ = E₂ψ₂.  Derive an expression for the specific heat per particle c_V = ∂<E>/∂T of the system as a function of temperature.

Solution:

• Concepts:
  Boltzmann statistics
• Reasoning:
  The system consisting of many particles is in a statistical mixture of states.
  In thermodynamic equilibrium P(E_i) ∝ g_iexp(-E_i/(kT)
  Here the degeneracy g_i is 1 for all i.
• Details of the calculation:
  Average energy:  <E> = (E₁ exp(-E₁/(kT)) + E₂ exp(-E₂/(kT)))/(exp(-E₁/(kT)) + exp(-E₂/(kT)))
  <E> = (E₁ exp(-βE₁) + E₂ exp(-βE₂))/(exp(-βE₁) + exp(-βE₂))
  = (E₁ + E₂ exp(-β∆))/(1 + exp(-β∆)),
  with β = 1/(kT) and ∆ = E₂ - E₁.
  c_V = ∂<E>/∂T.  c_V = (∂<E>/∂β)(∂β/∂T) = -(1/(kT²))∂<E>/∂β.
  c_V = [1/(kT²)][(E₂∆exp(-β∆))/(1 + exp(-β∆)) - (E₁ + E₂exp(-β∆))(∆exp(-β∆)))/(1 + exp(-β∆))²].

Problem:

Consider a system of N particles with only 3 possible energy levels separated by ε.  Let the ground state energy be zero.  The system occupies a fixed volume V and is in thermal equilibrium with a reservoir at temperature T.  Ignore interactions between particles and assume Boltzmann statistics apply.

(a)  What is the partition function for a single particle in the system?
(b)  What is the average energy per particle?
(c)  What is the probability that the 2ε level is occupied in the high-temperature limit k_BT >> ε?
Explain your answer on physical grounds.
(d)  What is the average energy per particle in the high-temperature limit k_BT >> ε?
(e)  At what energy is the ground state 1.1 times as likely to be occupied as the 2ε level?
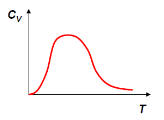
(f)  Find the heat capacity C_V of the system, analyze the low-T (k_BT >> ε) and high-T (k_BT >> ε) limit, and sketch CV as a function of T.

Solution:

• Concepts:
  Boltzmann statistics
• Reasoning:
  In thermodynamic equilibrium P(E_i) ∝ g_iexp(-E_i/(kT).
  Here the degeneracy g_i is 1 for all i.
• Details of the calculation:
  (a)  P(E) = Cexp(-E/(k_BT)).
  Σ_jP(E_j) = CΣ_jexp(-E_j/(k_BT)) = 1, C = 1/Σ_jexp(-E_j/(k_BT)) = 1/Z.
  Let β = 1/(k_BT)).
  Z = 1 + exp(-βε) + exp(-2βε).
  (b)  <ε> = (ε exp(-βε) + 2ε exp(-2βε))/Z
  = ε(exp(-βε) + 2exp(-2βε))/(1 + exp(-βε) + exp(-2βε)).
  (c)  P =  exp(-2βε)/(1 + exp(-βε) + exp(-2βε)) ~ (1 - 2βε)/( 1 + 1 - βε + 1 - 2βε) = 1/3.
  In the high energy limit the probability is the same for all three levels.
  (d)  <ε> = 0/3 + ε/3 + 2ε/3 = ε.
  (e)  exp(-2βε) = 1/1.1,  2βε = ln(1.1),  T = 2ε/(k_B*ln(1.1)).
  (f)  C_V = dU/dT = Nd<ε>/dT = Nd<ε>/dβ)(dβ/dT).
  C_V = (Nε²/(k_BT²))[ exp(-βε) + 4 exp(-2βε) + exp(-3βε)]/[1 + exp(-βε) + exp(-2βε)]².
  Low temperature limit:  C_V = (Nε²/(k_BT²)) exp(-ε/(k_BT)).  (C_V --> 0 as T --> 0)
  High temperature limit:  C_V = (2/3)(Nε²/(k_BT²)).  ( C_V --> 0 as T --> ∞)