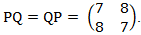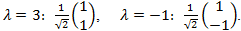Commuting and non-commuting observables

Calculating commutators

Problem:

Consider the operators whose action is defined by the equations below:
O₁ψ(x) = x³ψ(x)
O₂ψ(x) = x dψ(x)/dx
Find the commutator [O₁, O₂].

Solution:

• Concepts:
  Commutator algebra
• Reasoning:
  We are asked to find the commutator of two given operators.
• Details of the calculation:
  [O₁, O₂]ψ(x) = O₁O₂ψ(x)  - O₂O₁ψ(x)
  = O₁xdψ(x)/dx  - O₂x³ψ(x) = x⁴dψ(x)/dx  - xd(x³ψ(x))/dx
  = x⁴dψ(x)/dx  - 3x³ψ(x)  - x⁴dψ(x)/dx
  = -3x³ψ(x) = -3O₁ψ(x)  for any ψ(x).
  Therefore [O₁, O₂] = -3O₁.

Problem:

Let P and Q be two linear operators and let [P,Q] = -iħ.  Find
(a)  [Q,P],
(b)  [Q,Pⁿ],
(c)  [P,Qⁿ] .

Solution:

• Concepts:
  Commutator algebra
• Reasoning:
  We are asked to find several commutators.
  The product of two linear operators A and B, written AB, is defined by
  AB|Ψ> = A(B|Ψ>).
  The order of the operators is important. 
  The commutator [A,B] is by definition [A,B] = AB - BA.
  Two useful identities using commutators are 
  [A,BC] = B[A,C] + [A,B]C and [AB,C] = A[B,C] + [A,C]B.
  Proof: [A,BC] = ABC - BCA + (BAC - BAC) = ABC + B[A,C] - BAC = B[A,C] + [A,B]C.
• Details of the calculation:
  (a)  [Q,P] = iħ,  [Q,P²] = P[Q,P] + [Q,P]P = 2iħP.
  
  (b)  [Q,Pⁿ⁺¹] = [Q,PPⁿ] = P[Q,Pⁿ] + [Q,P]Pⁿ.
  If [Q,Pⁿ]  =iħnP^n-1, then [Q,Pⁿ⁺¹] = PiħnP^n-1 + iħPⁿ = iħ(n+1)Pⁿ.
  [Q,Pⁿ] = iħnP^n-1 holds for n = 1 and n = 2.  Therefore it holds for all n.
  
  (c)  [P,Q] = -iħ,  [P,Q²] = Q[P,Q] + [P,Q]Q = -2iħQ.
  [P,Qⁿ⁺¹] = [P,QQⁿ] = Q[P,Qⁿ] + [P,Q]Qⁿ.
  If [P,Qⁿ] = -iħnQ^n-1, then [P,Qⁿ⁺¹] = -QiħnQ^n-1 - iħQⁿ =- iħ(n+1)Qⁿ.
  [P,Qⁿ] = -iħnQ^n-1 holds for n = 1 and n = 2.  Therefore it holds for all n.

Problem:

Consider a one-dimensional system, with momentum operator p and position operator q.
(a) Show that [q,pⁿ] = iħ n p^n-1.
(b) Show that [q,F(p)] = iħ ∂F/∂p, if the function F(p) can be defined by a finite polynomial or convergent power series in the operator p.
(c) Show that [q,p²F(q)] = 2iħ pF(q) if F(q) is some function of q only.

Solution:

• Concepts:
  Commutator algebra
• Reasoning:
  We are asked to find several commutators.
• Details of the calculation:
  (a)  [q,p] = iħ,  [q,p²] = p[q,p] + [q,p]p = 2iħp.
  [q,pⁿ⁺¹] = [q,ppⁿ] = p[q,pⁿ] + [q,p]pⁿ.
  If [q,pⁿ]  =iħnp^n-1, then [q,pⁿ⁺¹] = piħnp^n-1 + iħpⁿ = iħ(n+1)pⁿ.
  [q,pⁿ] = iħnp^n-1 holds for n = 1 and n = 2.  Therefore it holds for all n.
  (b)  [q,F(p)] =  [q,∑_nf_npⁿ] = ∑_nf_n[q,pⁿ] = ∑_nf_nniħp^n-1] = iħ∂f(q)/∂q.
  Similarly,  [p,F(q)] =  [p,∑_nf_nqⁿ] = ∑_nf_n[p,qⁿ] = -∑_nf_nniħq^n-1] = -iħ∂f(q)/∂q.
  (c)  [q,p²F(q)] = p²[q,F(q)] + [q,p²]F(q)] = 0 + 2iħ pF(q).
  FYI:
  These formulas are used to proof the Ehrenfest's theorem.
  (d/dt)<R> = <P>/m.
  (d/dt)<P> = -<∇U(R)>.
  md²<R>/dt² = d<P>/dt = -<∇U(R)>.

Problem:

The operators P and Q are represented by matrices in some basis.

(a)  Do P and Q commute?
(b)  Find the normalized eigenvectors of P and Q.

Solution:

• Concepts:
  Commuting operators
• Reasoning:
  If the operators commute and the eigenvalues are not degenerate, they will have the same eigenvectors.
• Details of the calculation:
  (a)  The operators commute.
  
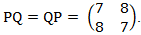
  (b)  To find the eigenvalues we calculate det(P - λI) and set it equal to zero.
  Eigenvalues of P:  (1 - λ)² - 4 = 0, λ₁ = 3,  λ₂ = -1.
  Associated eigenvectors:
  
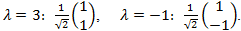
  Eigenvalues of Q:  (3 - λ)² - 4 = 0, λ₁ = 5,  λ₂ = 1.
  Associated eigenvectors:
  
  P and Q have the same non-degenerate eigenvectors.

Problem:

The angular momentum operators {J_x, J_y, J_z} are central to quantum theory.  States are classified according to the eigenvalues of these operators when J is conserved by the respective Hamiltonian H.
(a)  What condition(s) is (are) necessary for all eigenstates of H to be eigenstates of J? 
An eigenstate of J is usually specified by |j,m_z>,
where J²|j,m_z>  =  j(j + 1)ħ²|j,m_z> and J_z|j,m_z> = m_zħ|j,m_z>.
(b)  We can substitute J_x or J_y for J_z in (a).  However a state cannot be simultaneously an eigenstate of J_z and J_x.  Derive the commutation relation for the angular momentum operators J_x and J_z, (i.e.  [J_x,J_z] = -iħJ_y) from the definition of the linear momentum operator.
(c)  Prove that it is indeed possible for a state to be simultaneously an eigenstate of J² = J_x² + J_y² +J_z² and J_z. 

Solution:

• Concepts:
  Commuting operators
• Reasoning:
  Two commuting observables can be measured simultaneously, i.e. the measurement of one does not cause loss of information obtained in the measurement of the other.  If we measure a complete set of commuting observables (C.S.C.O.), then the state of the system after the measurement is one element of an unique eigenbasis.  The results of the measurement specify the state completely.
• Details of the calculation:
  (a) It is possible to specify a common eigenbasis of two operators if they commute.  If one of the operators is non degenerate, then all of its eigenvectors are also eigenvectors of the other operator.  In order for all eigenstates of H to be eigenstates of J² and J_z we need [J²,H] = 0 and [J_z,H] = 0 and H is non degenerate.  (States with different j or m_z must have different energy eigenvalues E.)
  (b) Assume the classical relationship J = r × p.
  J_x = yp_z - zp_y,  J_y = zp_x - xp_z,  J_z = xp_y - yp_x.
  For the quantum mechanical operators we then have
  J_x = YP_z - ZP_y,  J_y = ZP_x - XP_z,  J_z = XP_y - YP_x.
  [J_x,J_z] = [YP_z - ZP_y,XP_y - YP_x] = [YP_z,XP_y] + [ZP_y,YP_x] - [YP_z,YP_x] - [ZP_y,XP_y]
                                                                                        0               0
  = [YP_z,X]P_y + X[YP_z,P_y] + [ZP_y,Y]P_x + Y[ZP_y,P_x]
          0                                                  0
  = Z[P_y,Y]P_x +  X[Y,P_y]P_z = -iħ(ZP_x - XP_z) = -iħJ_y.
  
  (In general [J_i,J_j] = iħε_ijkJ_k.)
  (c) J² = J_x² + J_y² + J_z².  If [J²,J_z] = 0 then it is possible to find simultaneous eigenstates.
  [J²,J_z] = [J_x²,J_z] +  [J_y²,J_z] + [J_z²,J_z] = J_x[J_x,J_z] + [J_x,J_z]J_x + J_y[J_y,J_z] + [J_y,J_z]J_y
  = -iħ(J_xJ_y + J_yJ_x) + iħ(J_xJ_y + J_yJ_x) = 0.

Problem:

Show that if any operator commutes with two of the components of an angular momentum operator, it commutes with the third.

Solution:

• Concepts:
  The commutation relations for the Cartesian components of any angular momentum operator
• Reasoning:
  Commutation relations are what defines a vector operator as a angular momentum operator.  We define angular momentum through [J_i,J_j] = ε_ijkiħJ_k.

• Details of the calculation:
  Let  i ≠ j,k   j ≠ k and let i, j, k be cyclic ( x, y, z  or  y, z, x  or  z, x, y ).
  Then  [J_i,J_j] = iħJ_k, J_iJ_j - J_jJ_i = iħJ_k.
  Let A be an operator.
  Assume [J_i,A] = 0,  [J_j,A] = 0.  Then [A, J_k] = (1/iħ)[A,J_iJ_j - J_jJ_i].
  iħ[A, J_k] = [A,J_iJ_j] - [A,J_jJ_i] = [A,J_i]J_j + J_i[A,J_j] - [A,J_j]J_i - J_j[A,J_i] = 0.

Problem:

Consider the observables A = x² and B = L_z.
Construct the generalized uncertainty relation
ΔA ΔB ≥ ½|<i[A,B]>|,
(i.e. find the commutator), for these observables.

Solution:

• Concepts:
  Commutator algebra
• Reasoning:
  L_z = (r×p)_z = xp_y - yp_x, [r_i,p_j] = iħδ_ij.
• Details of the calculation:
  [x²,L_z] = x[x,L_z] + [x,L_z]x.
  [x,L_z] = [x,xp_y] - [x,yp_x] = -y[x,p_x] = -iħy.
  [x²,L_z]= -iħ[xy + yx] = -2iħxy.
  Δx²ΔL_z ≥  ħ|<xy>|.

Consequences

Problem:

Consider a system with Hamiltonian H.  Two observables A and B commute with H, [H,A] = [H,B] = 0, but do not commute with each other, [A,B] ≠ 0.  Show that the system has degenerate energy level.

Solution:

• Concepts:
  Commuting observables
• Reasoning:
  If two observables commute, a common eigenbasis can be found.  If they do not commute, then no common eigenbasis exists.
• Details of the calculation:
  [H,A] = 0, an eigenstate with a non-degenerate eigenvalue of H is also an eigenstate of A.
  [H,B] = 0, an eigenstate with a non-degenerate eigenvalue of H is also an eigenstate of B.
  All non-degenerate eigenstates of H are also eigenstates of A and B.
  [A,B] ≠ 0.  There are eigenstates of H and A that are not eigenstates of B and there are eigenstates of H and B that are not eigenstates of A.  The eigenstates of H must be degenerate.

Problem:

Let A and B be two observables (Hermitian operators).  In any state of the system
ΔAΔB ≥ ½|<i[A,B]>|. 
(a)  Prove this generalized uncertainty principle.
[Hint: Let |ψ> be any state vector and let A₁ = A - <A>I  and  B₁ = B - <B>I. 
Let |Φ> = A₁|ψ> + ixB₁|ψ> with x an arbitrary real number.  Use <Φ|Φ>  ≥  0.]

Now consider a single particle in an eigenstate of L² with wave function Ψ(r,t).
(b)  Calculate the commutators [sinφ, L_z] and [cosφ, L_z], where φ is the azimuthal angle.
(c)  Use these commutation relations and the result from part (a) to obtain uncertainty relations between sinφ, L_z and cosφ, L_z.
Note:  You can complete parts (b) and (c) without completing part (a).

Solution:

• Concepts:
  Generalized uncertainty principle, commutator algebra

• Reasoning:
  The hint leads to one way of proofing the generalized uncertainty principle.  There are certainly different ways to get the same result.

• Details of the calculation:
  (a)  <Φ|Φ> = <ψ|A₁²|ψ> + x²<ψ|B₁²|ψ> - ix<ψ|B₁A₁|ψ> + ix<ψ|A₁B₁|ψ>
  = <A₁²> + x²<B₁²> + x<ψ|i[A₁,B₁] ψ> = (ΔA)² + x²(ΔB)²  +  x<i[A,B]>
  for all x. 
  But <Φ|Φ>≥  0.  Therefore (ΔA)² + x²(ΔB)² + x<i[A,B]> ≥ = 0 for all x.
  For this to be true we either need that the quadratic equation y = ax² + bx + c either has no zeros, or is equal to zero for only one value of x.  (The equation describes a parabola.  The vertex of the parabola can either touch the x-axis or must lie above the x-axis.) 
  To find a root we set  x = [-b ± (b²  - 4ac)^½]/(2a) . 
  If b² < 4ac the equation has no roots.  If b²  = 4ac or x = -b/2a  the equation is zero.  We therefore need 4ac ≥ b².  Therefore ΔAΔB ≥ ½|<i[A,B]>|. 
  (b)  In spherical coordinates the L_z operator is L_z = (ħ/i)(∂/∂φ)
  [sinφ, L_z]Ψ = (ħ/i) sinφ (∂Ψ/∂φ) -  (ħ/i) cosφ Ψ - (ħ/i) sinφ (∂Ψ/∂φ) = - (ħ/i) cosφ Ψ
  for any wave function Ψ .  Therefore [sinφ, L_z] = - (ħ/i) cosφ.
  Similarly, [cosφ, L_z] = (ħ/i) sinφ.
  (c)  The generalized uncertainty relation:  ΔAΔB ≥ ½|<i[A,B]>|.
  Δsinφ ΔL_z ≥ ½ |< i [ sinφ, L_z]>| = -(ħ/2) |< cosφ >|
  Δcosφ ΔL_z ≥ ½ |< i [ cosφ, L_z]>| = (ħ/2) |< sinφ >|
  If Ψ(r,t) is an eigenstate of L², i.e. if |L| is known, then Δsinφ ΔL_z = Δcosφ ΔL_z ≥ 0.
  Since L² and L_z commute, the particle can be in an eigenstate of L_z.  Then ΔL_z = 0. 
  Since 1 ≥  cosφ ≥ -1 and 1 ≥  sinφ ≥ -1, (Δsinφ ΔL_z)_min = (Δcosφ ΔL_z)_min = 0 for an eigenstate of L_z.