Eigenvalues and eigenfunctions

Find eigenvalues and eigenfunctions

Problem:

Consider a 3-dimensional state space with orthonormal eigengbasis {|a>, |b>, |c>}.  The action of the Hamiltonian on the basis vectors is
H|a> = -iE|b> + iE|c>,  H|b> = iE|a>,  H|c> = -iE|a>, where E is a real constant with units of energy.
(a)  Construct the matrix of the Hamiltonian in the {|a>, |b>, |c>} basis.
(b)  Find the energy eigenvalues and the corresponding normalized eigenvectors.

Solution:

• Concepts:
  The eigenvalues and eigenvectors of a Hermitian operator.
• Reasoning:
  We are given enough information to construct the matrix of the Hermitian operator H in some basis.  To find the eigenvalues E we set the determinant of the matrix (H - EI) equal to zero and solve for E.  To find the corresponding eigenvectors {|Ψ>}, we substitute each eigenvalue E back into the equation (H-E*I)|Ψ> = 0 and solve for the expansion coefficients of |Ψ> in the given basis.
• Details of the calculation:
  (a)  <a|H|a> = <b|H|b> = <c|H|c> = <b|H|c> = <c|H|b> = 0.
  <a|H|b> = <b|H|a>* = iE,  <c|H|a> = <a|H|c>* = iE.
  The matrix of the Hamiltonian in the given basis is
  .
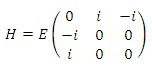  (b)  Denote the eigenvalues by αE.  To find α we solve
  
  .
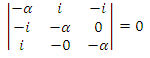  -α³ + 2α = 0,  α = 0, ±√2.
  (1)  eigenvalue 0:  0a₁ + ib₁ - ic₁ = 0, -ia₁ = 0.
  corresponding normalized eigenvector:  (1/√2)(|b> + |c>).
  (2)  eigenvalue √2E:  -√2a₂ + ib₂ - ic₂ = 0, -ia₂ - √2b₂ = 0.
  corresponding eigenvector:  (1/√2)|a> - (i/2)|b> + (i/2)|c>.
  (2)  eigenvalue -√2E:  √2a₃ + ib₃ - ic₃ = 0, -ia₃ + √2b₃ = 0.
  corresponding eigenvector:  (1/√2)|a> + (i/2)|b> - (i/2)|c>.

Properties and consequences

Problem:

Suppose |i> and |j> are eigenkets of some Hermitian operator A.  Under what conditions can we conclude that |i> + |j> is also an eigenket?  Justify your answer.

Solution:

• Concepts:
  Eigenvalues of operators
• Reasoning:
  An operator operating on the elements of the vector space V has certain kets, called eigenkets, on which its action is simply that of rescaling. 
  Ω|V> = ω|V>.  |V> is an eigenket (eigenvector) of Ω, ω is the corresponding eigenvalue.
• Details of the calculation:
  |i> and |j> are eigenkets of A.
  A|i> = a_i|i>,  A|j> = a_j|j>.
  A(|i> + |j>) = a_i|i> + a_j|j> ≠ a_ij(|i> + |j>) unless a_i = a_j, i.e.  unless |i> and |j> have the same eigenvalue.

Problem:

Consider a quantum system for which the exact Hamiltonian is H.  Assume the quantum system is of bounded spatial extend, so that it is known rigorously that the eigenstates of H, {|Ψ_n>}, are complete. 
(a) Show that if |Ψ_n> and |Ψ_m> are two eigenstates of H with eigenvalues E_n and E_m
with E_n ≠ E_m, then <Ψ_n|Ψ_m> = 0.
(b) Suppose E_n = E_m, with n ≠ m.  Can we still have <Ψ_n|Ψ_m> = 0 ?
(c) The problem H|Ψ> = E|Ψ> is very complicated but it is suggested that we use a trial function |Ψ_trial> for |Ψ> and approximate E by E = <Ψ_trial|H|Ψ_trial>/<Ψ_trial|Ψ_trial>.
Show that E > E₀, where E₀ is the lowest eigenvalue of H.

Solution:

• Concepts:
  Hermitian operators
• Reasoning:
  H is a Hermitian operator.  The eigenvalues of a Hermitian operator are real.  Every Hermitian operator has at least one basis of orthonormal eigenvectors. 
• Details of the calculation:
  (a)  H = H^T, H is a Hermitian operator
  <Ψ_n|H|Ψ_m> = E_m<Ψ_n|Ψ_m> =  <Ψ_n|H^T|Ψ_m> = E_n<Ψ_n|Ψ_m>.
  E_m<Ψ_n|Ψ_m> - E_n<Ψ_n|Ψ_m> = 0.  Since E_n ≠ E_m, <Ψ_n|Ψ_m> must be zero.
  (b)  Yes, an orthonormal basis for the state space can be formed by the eigenfunctions of any Hermitian operator.
  (c)  Any wave function can be expanded in terms of the eigenfunctions of H.
  |Ψ_trial> = ∑_na_n|Ψ_n>,  {|Ψ_n>} = orthonormal basis for the state space.
  H|Ψ_trial> = ∑_na_nE_n|Ψ_n>.
  <Ψ_trial|H|Ψ_trial> = ∑_na_nE_n<Ψ_trial|Ψ_n> = ∑_m∑_na_m*a_nE_n<Ψ_m|Ψ_n>
  = ∑_m∑_na_m*a_nE_nδ_mn<Ψ_n|Ψ_n> = ∑_n|a_n|²E_n<Ψ_n|Ψ_n> ≥ ∑_n|a_n|²E₀<Ψ_n|Ψ_n>
  since E₀ is the lowest eigenvalue.
  <Ψ_trial|H|Ψ_trial> ≥ E₀ ∑_n|a_n|²<Ψ_n|Ψ_n> = E₀<Ψ_trial|Ψ_trial>

Problem:

Consider two solutions to the one-dimensional time-independent Schroedinger equation with same energy E: ψ₁(x) and ψ₂(x).
(a)  Prove that regardless of the potential energy function U(x),

ψ₂(x) ∂ψ₁(x)/∂x - ψ₁(x) ∂ψ₂(x)/∂x = C,

where C is a constant.
(b)  By considering the boundary conditions, show that if ψ₁(x) and ψ₂(x) are bound state solutions, then C = 0.  From this, show that ψ₂(x)  = γ ψ₁(x) for some constant γ, thus proving that there are no degenerate bound state solutions to the one-dimensional time-independent Schroedinger equation.
(c)  Why does this theorem fail for continuum eigenstates (i.e. unbound states)?  Give a specific example of degenerate continuum eigenstates in one dimension.

Solution:

• Concepts:
  The time-independent Schroedinger equation in one dimension
• Reasoning:
  We are supposed to show that in 1 dimension bound state solutions of the Schroedinger equation are non-degenerate.
• Details of the calculation:
  (a)  Given:
  ∂²ψ₁(x)/∂x² - (2m/ħ²)(E - U(x))ψ₁(x) = 0.
  ∂²ψ₂(x)/∂x² - (2m/ħ²)(E - U(x))ψ₂(x) = 0.
  Multiplying the first equation by ψ₂(x) and the second equation by ψ₁(x) and subtracting we obtain ψ₂(x) ∂²ψ₁(x)/∂x² - ψ₁(x)∂²ψ₂(x)/∂x² = 0.
  ∂/∂x(ψ₂(x) ∂ψ₁(x)/∂x - ψ₁(x) ∂ψ₂(x)/∂x) = ψ₂(x) ∂²ψ₁(x)/∂x² - ψ₁(x)∂²ψ₂(x)/∂x² = 0.
  Therefore ψ₂(x) ∂ψ₁(x)/∂x - ψ₁(x) ∂ψ₂(x)/∂x = C. (Integration)
  (b)  For bound states the wave function must vanish as x --> ± ∞.  Therefore C = 0.
  ψ₂(x) ∂ψ₁(x)/∂x - ψ₁(x) ∂ψ₂(x)/∂x = 0.
  (1/ψ₁(x)) ∂ψ₁(x)/∂x = (1/ψ₂(x)) ∂ψ₂(x)/∂x.
  ∂/∂x(lnψ₁(x)) = ∂/∂x(lnψ₂(x)).
  This integrates to lnψ₁(x) = lnψ₂(x) + c,  ψ₂(x)  = γ ψ₁(x), where γ = e^c.
  ψ₂(x) can differ from ψ₁(x) only by a multiplicative constant.
  (c)  Continuum eigenstates do not necessarily vanish as x --> ± ∞, so C is not necessarily zero.
  Example: Let U(x) = 0, we have a free particle.
  ψ₁(x) = exp(i(2mE/ħ²)^½x) and ψ₂(x) = exp(-i(2mE/ħ²)^½x) are two degenerate continuum eigenstates.

Problem:

A particle of mass m moves in one dimension.  It is remarked that the exact eigenfunction for the ground state is Ψ(x) = A/cosh(λx), where λ is a constant, and A is the normalization constant.  Assuming that the potential U(x) vanishes at infinity, derive the ground state energy and also U(x). 

Solution:

• Concepts:
  The Schroedinger equation
• Reasoning:
  The given wave function is a solution of the 1-dimensional, time-independent Schroedinger equation.
• Details of the calculation:
  (-ħ²/2m)(∂²/∂x²)Ψ(x) + U(x)Ψ(x) = EΨ(x).
  (∂/∂x)(1/cosh(λx)) = -(sinh(λx)/cosh²(λx))λ.
  (∂²/∂x²)(1/cosh(λx)) = -(λ²/cosh(λx))[1 - 2sinh²(λx)/cosh²(λx)]
  (ħ²/2m)Aλ²/cosh(λx))[1 - 2sinh²(λx)/cosh²(λx)] + U(x)A/cosh(λx) = EA/cosh(λx).
  (ħ²λ²/2m)[1 - 2sinh²(λx)/cosh²(λx)] = E - U(x).
  As x --> ∞,  U(x) --> 0, and sinh(λx)/cosh(λx) --> 1.  Therefore E = -(ħ²λ²/2m).
  U(x) = -(ħ²λ²/m) + (ħ²λ²/m) sinh²(λx)/cosh²(λx)] = -(ħ²λ²/m)(1/cosh²(λx)])
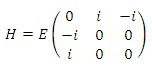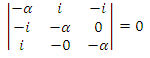