Evolution of probabilities

Problem:

I measure the observable A of a system in an arbitrary state |ψ>.  The result of the measurement is a.  What will the result be if I repeat the measurement immediately?   Do I get the same result if I first wait a while and then repeat the measurement?  Under what circumstance is the answer to this question "yes"?

Solution:

• Concepts:
  Postulates of quantum mechanics
• Reasoning:
  After the first measurement, the wave function is in an eigenstate of A with eigenvalue a, so after the immediate re-measurement, I find the same result.  If I wait a while, the state vector will evolve according to |ψ(t)> = e^−iHt/ħ|ψ>, which may no longer be an eigenstate of A (or it may be an eigenstate with a different eigenvalue).  However, if the Hamiltonian and A commute, the system will remain in the same eigenstate of A and even after a while, the measurement will still yield a.

Problem:

Consider two-flavor neutrino mixing. 
The energy (or mass) eigenstates

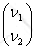
are related to the flavor eigenstates

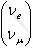
as  
. 

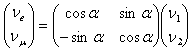The energy eigenvalues are E₁ and E₂, with E₁ ≠ E₂. 
Assume the system starts at time t = 0 in the electron-neutrino state

 . 

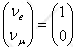What is the probabilities that at time t the system will be found in the μ-neutrino state

  ?

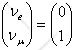Solution:

• Concepts:
  The evolution operator
• Reasoning:
  The evolution operator is a unitary operator defined through |ψ(t)> = U(t,t₀)|ψ(t₀)>.
  If H does not explicitly depend on time, then U(t,t₀) = exp(-(i/ħ)H(t - t₀)).
  If Ψ(t₀)> is an eigenfunction of H with eigenvalue E,
  then Ψ(t)> =  exp(-(i/ħ)E(t - t₀))Ψ(t₀)>.
• Details of the calculation:
  |Ψ(0)> = cosα|ν₁> + sinα|ν₂>.  Here |ν₁> and |ν₂> are eigenfunctions of H.
  |Ψ(t)> = exp(-iE₁t/ħ)cosα|ν₁> + exp(-iE₂t/ħ)sinα|ν₂>.
  The probabilities that at time t the system will be found in the μ-neutrino state is
  P_μ(t) = |<ν_μ|Ψ(t)>|²
  = |(-sinα< ν₁| + cosα< ν₂|)(exp(-iE₁t/ħ)cosα|ν₁> + exp(-iE₂t/ħ)sinα|ν₂>)|²
  = |(-sinα exp(-iE₁t/ħ)cosα + cosα exp(-iE₂t/ħ)sinα|²
  = 2sin²αcos²α - 2sin²αcos²α cos((E₁-E₂)t/ħ)
  = ½ sin²(2α) (1- cos((E₁-E₂)t/ħ))  = sin²(2α) sin²((E₁-E₂)t/(2ħ)).

Problem:

A box containing a particle is divided into right and left compartments by a thin partition.  If the particle is known to be on the right or left sides with certainty, the state is represented by the eigenkets |R> and |L>, respectively.  The particle can tunnel though the partition; this tunneling effect is characterized by the Hamiltonian
H = ∆(|L><R|+|R><L|),
where ∆ is a real number with the dimension of energy. 
Suppose that at time t = 0 the particle is on the right side with certainty. 
What is the probability for observing the particle on the left side as a function of time?

Solution:

• Concepts:
  The fundamental assumptions of quantum mechanics, the evolution operator
• Reasoning
  The particle is not in a stationary state.  We need to find the eigenstates of H and expand the state in terms of these eigenstates.
• Details of the calculation:
  Choose the {|R>, |L>} orthonormal basis.
  Let H₀|R> = E₀|R>, H₀|L> = E₀|L>, and choose the zero of the potential energy so that E₀ = 0.
  H = H₀ + H'.
  The matrix of H in the {|R>, |L>}basis is
  .
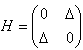  To find the eigenvalues of H we set
  .
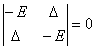  The eigenvalues are E₁ = ∆ and E₂ = -∆.
  The corresponding eigenvectors are |1> = 2^-½(|R> + |L>) and |2> = 2^-½(|R> - |L>).
  |ψ(0)> = |R> = 2^-½(|1> + |2>).
  |ψ(t)> = U(t,0)|ψ(0)> = 2^-½(|1>exp(-i∆t/ħ) + |2>exp(i∆t/ħ)).
  |ψ(t)> = ½[(|R> + |L>)exp(-i∆t/ħ) + (|R> - |L>)exp(i∆t/ħ))]
  = ½[|R>(exp(-i∆t/ħ) + exp(i∆t/ħ)) + |L>(exp(-i∆t/ħ) - exp(i∆t/ħ))]
  = |R>cos(∆t/ħ) - i|L>sin(∆t/ħ).
  The probability for observing the particle on the left side as a function of time is
  P_L(t) = |<L|ψ(t)>|² = sin²(∆t/ħ).

Problem:

A system is described by a Hamiltonian whose matrix is

.
in the {|1>, |2>} basis.  Here a = |a|exp(iφ).
(a)  Find the eigenvalues and normalized eigenvectors of this Hamiltonian.
(b)  Calculate the probability of finding the system in the state |1> at time t, if it was in the state |2> at t = 0.

Solution:

• Concepts:
  The eigenvalues and eigenvectors of a Hemitian operator, the evolution operator
• Reasoning:
  We are given the matrix of the Hermitian operator H in some basis.  To find the eigenvalues E we set the determinant of the matrix (H - EI) equal to zero and solve for E.  To find the corresponding eigenvectors {|α>}, we substitute each eigenvalue E back into the equation (H - EI)| α > and solve for the expansion coefficients of |α> in the given basis.
  The evolution operator is a unitary operator defined through |ψ(t)> = U(t,t₀)| ψ(t₀)>.
  If H does not explicitly depend on time, then U(t,t₀) = exp(-(i/ħ)H(t-t₀)).
  If |ψ(t₀)> is an eigenfunction of H with eigenvalue E, then |ψ(t)> =  exp(-(i/ħ)E(t-t₀))|ψ(t₀)>.
• Details of the calculation:
  (a)  The eigenvalues of H are E, where
  
  .
  
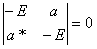  E² - |a|² = 0,  E = ±|a|.
  The normalized eigenstates of H are |±> =  A₁|1> + A₂|2>.
  For E = |a| we have -|a|A₁ + aA₂ = 0, A₂ = (|a|/a)A₁ = exp(-iφ)A₁. 
  |+> = 2^-½|1> + 2^-½exp(-iφ)|2>.
  For E = -|a| we have |a|A₁ + aA₂ = 0, A₂ = -(|a|/a)A₁ = -exp(-iφ)A₁. 
  |-> = 2^-½|1> - 2^-½exp(-iφ)|2>.
  (b)  |ψ(t)> = exp(-iHt/ħ)|2>.  P₁(t) = |<1|ψ(t)>|².
  |1> = 2^-½(|+> + |->),  |2> = 2^-½(|+> - |->).
  Global phase factors are irrelevant.
  |ψ(t)> = 2^-½(exp(-i|a|t/ħ)|+> - exp(i|a|t/ħ)|->). 
  <1|ψ(t)> = ½(exp(-i|a|t/ħ) - exp(i|a|t/ħ))= -i sin(|a|t/ħ).
  P₁(t) = sin²(|a|t/ħ).

Problem:

Consider a three-state quantum mechanical system with an orthonormal 'color' basis {|R>, |G>, |B>} ('red,' 'blue,' and 'green' respectively).  Its evolution is governed by the Hamiltonian
H = E₀(2|R><R| + 2|B><B| + 2|G><G| - |G><B| - |B><G|).
(a)  Construct the matrix representation of this Hamiltonian using the {|R>, |G>, |B>} basis.
(b)  Find the energy eigenvalues and normalized eigenstates of the system.  Express the latter as linear combinations of |R>, |G>, |B>.
(c)  At time t = 0 the state vector is |ψ(0)> = |G>.  Find the state vector |ψ(t)> at an arbitrary time t.
(d)  After starting from the initial conditions of (c), the 'color' is measured at time t = t₀ and found to be green.  What are the probabilities for the color to be measured as red, green, or blue at time t = 2t₀?

• Concepts:
  Eigenvalues and eigenvectors, the evolution operator.
• Reasoning:
  We are asked to find the eigenvalues and eigenvectors of a given Hamiltonian H.
  We are then asked to find |ψ(t)> given |ψ(0)>. 
  We expand |ψ(0)> in terms of eigenvectors of H and apply the evolution operator.
• Details of the calculation:
  (a)  The matrix of H in the {|R>, |G>, |B>} basis is

  .

  (b)  The eigenvalues λE₀ are found from

  .

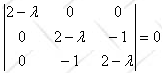  (2 - λ)³ - (2 - λ) = 0.  The eigenstates are A₁|R> +A₂|B> + A₃|G>.
  (i)  (2 - λ) = 0,  λ₁ = 2.  A₃ = A₂ = 0, A₁ = 1,  |1> = |R>.
  (ii)  (2 - λ)² = 1,  (2 - λ) = 1,  λ₂ = 1.  A₃ = A₂ = 1/√2, A₁ = 0, |2> = (|B> + |G>)/√2.
  (iii)  (2 - λ) = -1,  λ₃ = 3.  A₃ = -A₂ = 1/√2, A₁ = 0,  |3> = (|B> - |G>)/√2.

  (c)  |B> = (|2> + |3>)/√2.  |G> = (|2> - |3>)/√2.  |ψ(0)> = |G> =  (|2> - |3>)/√2. 
  |ψ(t)> = (exp(-iλ₂E₀t/ħ)|2> - exp(-iλ₃E₀t/ħ)|3>)/√2
  = (exp(-iE₀t/ħ)|2> - exp(-i3E₀t/ħ)|3>)/√2 
  = exp(-i2E₀t/ħ)((exp(iE₀t/ħ)|2> - exp(-iE₀t/ħ)|3>)/√2
  = exp(-i2E₀t/ħ)((exp(iE₀t/ħ)(|B> + |G>) - exp(-iE₀t/ħ)(|B> - |G>))/2
  = exp(-i2E₀t/ħ)(i(sin(E₀t/ħ)|B> + cos(E₀t/ħ)|G>)).

  (d)  After the measurement at t₀ we have |ψ(t₀)> = e^iφ|G>.
  At t = 2t₀ the probability for a color to be measured green is the same as the probability for this color to be measured at t = t₀.
  P_G(2t₀) = cos²(2E₀t/ħ),  P_B(2t₀) = sin²(2E₀t/ħ),  P_R(2t₀) = 0. 

Problem:

A quantum system can exist in two states |ψ₁> and |ψ₂>, which are eigenstates of the Hamiltonian with eigenvalues E₁ and E₂. 
An observable A has eigenvalues ±1 and eigenstates |ψ_±>= (1/√2)(|ψ₁> ± |ψ₂>).
This observable is measured at times t = 0, T, 2T, ... .  The normalized state of the system at t = 0, just before the first measurement, is c₁|ψ₁> + c₂|ψ₂>. 
(a)  What is the probability of measuring A = 1 at t = 0?
(b)  If P_n denotes the probability that the measurement at t = nT gives the result A = 1, show that P_n+1 = ½(1 - cosα) + P_n cosα, where
α = (E₁ - E₂)T/ħ.
(c)  Deduce that  P_n = ½ (1 - cosⁿα) + ½|c₁ + c₂|² cosⁿα.
(d)  What happens in the limit as n --> ∞ with nT = t fixed?

Solution:

• Concepts:
  The fundamental assumptions of quantum mechanics, the evolution operator
• Reasoning:
  When a physical quantity described by the operator A is measured on a system in a normalized state |Ψ>, the probability of measuring the eigenvalue a_n is given by
  P(a_n) = ∑_i=0^gn|<u_nⁱ|Ψ>|²,  where {|u_nⁱ>} (i=1,2,...,g_n) is an orthonormal basis in the eigensubspace Ε_n associated with the eigenvalue a_n.
• Details of the calculation:
  (a)  The probability of measuring A = 1 at t = 0 is
  P₀ = ½|(<ψ₁| + <ψ₂|)(c₁|ψ₁> + c₂|ψ₂>)|² =  ½|c₁ + c₂|².
  (b)  Before the first measurement at t = 0, |ψ(0)> = c₁|ψ₁> + c₂|ψ₂>.   After each measurement the state is either |ψ₊> or |ψ_->.  The probability that after the nth measurement the state is |ψ₊> is P_n, the probability that the state is |ψ_-> is 1 - P_n.
  (i)  Assume that after the nth measurement the system is in state |ψ₊>.
  After a time interval T we have  |ψ> = 2^-½(exp(-E₁T/ħ)|ψ₁> + exp(-E₂T/ħ)|ψ₂>).
  The probability of measuring A = 1 is |<ψ₊|ψ>|² = ¼|exp(-E₁T/ħ) + exp(-E₂T/ħ)|².
  (ii)  Assume that after the nth measurement the system is in state |ψ_->.
  After a time interval T we have  |ψ> = 2^-½(exp(-E₁T/ħ)|ψ₁> - exp(-E₂T/ħ)|ψ₂>).
  The probability of measuring A = 1 is |<ψ₊|ψ>|² = ¼|exp(-E₁T/ħ) - exp(-E₂T/ħ)|².
  The total probability of measuring A = 1 is
  P_n+1 = P_n ¼|exp(-E₁T/ħ) + exp(-E₂T/ħ)|² + (1 - P_n) ¼|exp(-E₁T/ħ) - exp(-E₂T/ħ)|²
  = P_n ½(1 + cos((E₁ - E₂)T/ħ)) + (1 - P_n) ½(1 - cos((E₁ - E₂)T/ħ))
  = P_n ½(1 + cos(α)) + (1 - P_n) ½(1 - cos(α)) = ½(1 - cosα) + P_n cosα.
  (c)  P₁ = ½(1 - cosα) + P₀ cosα.
   P₂ = ½(1 - cosα) + P₁ cosα = ½(1 - cosα) + ½(1 - cosα)cosα + P₀ cos²α
  = ½(1 - cosα²) + P₀ cos²α.
  Assume P_n = ½(1 - cosⁿα) + P₀cosⁿα.  This holds for P₁ and P₂.
  Then P_n+1 = ½(1 - cosα) + P_n cosα = ½(1 - cosα) + (½(1 - cosⁿα) + P₀cosⁿα)cosα
   = ½(1 - cos⁽ⁿ⁺¹⁾α) + P₀cos⁽ⁿ⁺¹⁾α.
  If  P_n = ½(1 - cosⁿα) + P₀cosⁿα  holds for n, it also holds for n + 1.
  (d)  As n --> ∞,  cosⁿα  --> 1, P_n --> P₀.  (Quantum Zeno Effect)
  Continuously measuring suppresses the evolution of the system.

Problem:

A particle in a potential well U(x) is initially in a state whose wave function is an equal-weight superposition of the ground state and first excited state wave functions
Ψ(x,0) = C[ψ₁(x) + ψ₂(x)],
where C is a constant and ψ₁(x) and ψ₂(x) are normalized solutions to the time-independent Schroedinger equation with energies E₁ and E₂. 
(a)  Show that the value C = 1/√2  normalizes Ψ(x,0).
(b)  Determine Ψ(x,t) at any later time t.
(c)  Show that the average energy <E> for Ψ(x,t) is the arithmetic mean of the energies E₁ and E₂. 
(d)  Determine the uncertainty ∆E of the energy for Ψ(x,t).

Solution:

• Concepts:
  The postulates of Quantum Mechanics, the mean value
• Reasoning:
  The wave function is not an eigenstate of the Hamiltonian.  We are asked to normalize it, evolve it, and to find <E> and ∆E.
• Details of the calculation:
  (a)  Eigenfunctions of the Hermitian operator H with different eigenvalues are orthogonal.  Therefore ψ₁ and ψ₂ are orthonormal.
  ∫_-∞^+∞dx |Ψ(x,0)|² = 1 --> |C|²[∫_-∞^+∞dx |ψ₁(x)|²  + ∫_-∞^+∞dx |ψ₂(x)|²] = 2|C|² = 1.
  C = 2^-½e^iφ is the most general solution.  C = 2^-½  normalizes Ψ(x,0).
  (b)  Ψ(x,t) = U(t,0) Ψ(x,t) = 2^-½exp(-iHt/ħ)[ψ₁(x) + ψ₂(x)]
  = 2^-½[exp(-iE₁t/ħ)ψ₁(x) + exp(-iE₂t/ħ)ψ₂(x)].
  (c)  <E(t)> = ∫_-∞^+∞dx Ψ*(x,t)H Ψ(x,t).
  HΨ(x,t) = 2^-½[exp(i( E₁)t/2ħ) E₁ ψ₁(x) + exp(-iE₂t/2ħ) E₂ ψ₂(x)].
  ∫_-∞^+∞dx Ψ*(x,t) HΨ(x,t) = ½(E₁∫_-∞^+∞dx |ψ₁(x)|² + E₂∫_-∞^+∞dx |ψ₂(x)|²] = ½(E₁ + E₂).
  (d)  ∆E = (<E²> - <E>²)^½.
  <E²> = ∫_-∞^+∞ dx HΨ*(x,t) HΨ(x,t) = ½(E₁² + E₂²).
  <E>² = ¼(E₁² + E₂² - 2E₁E₂).
  ∆E = (¼E₁² + ¼E₂² - ½E₁E₂)^½.

Problem:

(a)  Define what is meant by the term "stationary state" in quantum mechanics, and explain the distinction between the time-dependent and time-independent Schroedinger equation.
(b)  At time t = 0, the wave function of a particle in one dimension is ψ(x) = (u₁(x) + u₂(x))/√2, where u₁(x) and  u₂(x) are two solutions of the time-independent Schroedinger equation.  
For this particle, how does the probability density change with time?

Solution:

• Concepts:
  The Schroedinger equation
• Reasoning:
  We must distinguish between the general solutions of the Schroedinger equation and the special solutions which are energy eigenstates.
• Details of the calculation:
  (a)  A stationary state is an eigenstate of the energy operator iħ∂ψ(r,t)/∂t = Eψ(r,t) and therefore of the Hamiltonian H.  Stationary states can be written as ψ(r,t) = ψ(r) exp(-iEt/ħ), and |ψ(r,t)|² = ψ(r) exp(-iEt/ħ) ψ^*(r) exp(iEt/ħ) = ψ(r)ψ^*(r) = |ψ(r)|² is independent of time.  (Hence the name!)  The time-independent Schroedinger equation is the eigenvalue equation for H.  The time-dependent Schroedinger equation describes the time-evolution of any state vector or wave function, i.e. of any superposition of energy eigenfunctions with different energy eigenvalues.
  
  (b) ψ(x,t) = 2^-½[u₁(x,t) + u₂(x,t)], where
  u₁(x,t) = u₁(x) exp(-(2πi/h)E₁t) and u₂(x,t) = u₂(x) exp(-(2πi/h)E₂t).
  P(x,t) = |ψ(x,t)|² is the probability per unit length of finding the particle at position x.

  |ψ(x,t)|² = ½|u₁(x,t) + u₂(x,t)|²
  Plug in u₁(x,t) and u₂(x,t).
  |ψ(x,t)|² = u₁(x) exp(-(2πi/h)E₁t) + u₂(x) exp(-(2πi/h)E₂t)|²
  = (u₁(x) exp(-(2πi/h)E₁t) + u₂(x) exp(-(2πi/h)E₂t))
  * (u₁^*(x) exp((2πi/h)E₁t) + u₂^*(x) exp((2πi/h)E₂t))
  = ½ [|u₁(x) |² + |u₁(x) |² + (u₁(x) u₂^*(x) exp(i2π(E₂-E₁)t/h) + u₁^*(x) u₂(x) exp(-2iπ(E₂-E₁)t/h)]
  = ½ [|u₁(x) |² + |u₁(x) |² + 2|u₁(x) u₂(x)| cos(2π(E₂-E₁)t/h + φ)],
  where we write u₁(x) u₂^*(x) = |u₁(x) u₂(x)| exp(iφ)

  P(x,t) = ½ [|u₁(x) |² + |u₁(x) |² + 2|u₁(x) u₂(x)| cos(2π(E₂-E₁)t/h + φ)].
  The probability per unit length of finding the particle at x changes with time.  It oscillates.

Problem:

Consider a quantum particle for which the Hamiltonian operator is H.  Denote by |Φ_n> the eigenvectors of H, corresponding to the energy eigenvalues E_n.  Assume that the |Φ_n> form a complete, orthonormal basis.  At time t = 0 the particle is in the state

|Ψ> = A[|Φ₀> + 2i|Φ₁> + 4|Φ₃> - 2|Φ₄>].

(a)  Normalize |Ψ>.
(b)  Imagine that you perform an experiment to measure the energy of the system.  What is the most likely result of this measurement and what is the probability of getting this result?
(c)  What is the expectation value of the energy <H>?
(d)  Find |Ψ(t)>.

Solution:

• Concepts:
  The postulates of Quantum Mechanics, the mean value
• Reasoning:
  When a physical quantity described by the operator A is measured on a system in a normalized state |ψ>, the probability of measuring the eigenvalue a_n is given by
  P(a_n) = Σ_i=0^gn|<u_nⁱ|ψ>|²,  where {|u_nⁱ>} (i=1,2,...,g_n) is an orthonormal basis in the eigensubspace E_n associated with the eigenvalue a_n.
  If a measurement on a system in the state |ψ> gives the result a_n, then the state of the system immediately after the measurement is the normalized projection of |ψ> onto the eigensubspace associated with a_n.
• Details of the calculation:
  (a)  Normalization:  <Ψ|Ψ> = |A|²(|1|² + |2i|² + |4|² + |-2|²) = 25|A|² = 1.  A = 1/5 if we choose it real and positive.
  (b)  |Ψ> = (1/5)|Φ₀> + (2i/5)|Φ₁> + (4/5)|Φ₃> - (2/5)|Φ₄>.
  P(E₀) = ½5,  P(E₁) = 4/25,  P(E₃) = 16/25,  P(E₄) = 4/25.  The most likely result is E₂.
  (c)  <H> = (½5)(E₀ + 4 E₁ + 16 E₃ + 4 E₄).
  (d)  |Ψ> = (1/5)|Φ₀>exp(-iE₀t/ħ) + (2i/5)|Φ₁>exp(-iE₁t/ħ) + (4/5)|Φ₃>exp(-iE₃t/ħ) - (2/5)|Φ₄exp(-iE₄t/ħ)>.
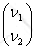
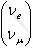
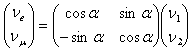
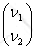
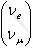
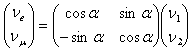
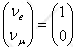
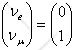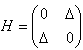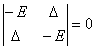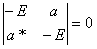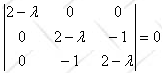