Mathematical foundations

Problem:

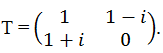
Let Ω be the operator defined bψ Ω = |Φ><ψ| where |Φ> and |ψ> are two vectors in a vector space V.
(a)  Under what conditions is Ω Hermitian?
(b)  Calculate Ω².  Under what conditions is Ω a projector?

Solution:

• Concepts:
  Mathematical foundations of quantum mechanics
• Reasoning:
  An operator A is Hermitian if A = A^†. A Hermitian operator satisfies <ψ|A|Φ> = <Φ|A|ψ>*.
  A projector is a Hermitian operator.  If Ω is a projector, then Ω² = Ω.
• Details of the calculation:
  (a)  Ω = |Φ><ψ|, Ω^† = |ψ><Φ|.
  Ω = Ω^†  -->  Ω|ζ> = Ω^†|ζ>  for any |ζ> in V.
  We need |Φ><ψ|ζ> = |ψ><Φ|ζ>.  This implies |Φ> = a|ψ>.
  Then a|ψ><ψ|ζ> = |ψ><Φ|ζ> or a<ψ|ζ> =  <Φ|ζ>.
  But we also have <Φ|ζ> = a*<ψ|ζ>.
  Therefore a = a*.
  We need |Φ> = a|ψ>, with a real.
  (b) Ω² = |Φ><ψ|Φ><ψ|.  We need <ψ|Φ> = 1 and |Φ> = a|ψ>. 
  This implies a<ψ|ψ> = 1, a = 1/<ψ|ψ>.

Problem:

Quantum mechanics is often conveniently formulated in terms of matrix operators.  Let {|i>} be an orthonormal basis for the state space.
(a)  Prove that for any operator A we have ∑_ij|<i|A|j>|² = Tr(AA^†), where Tr denotes the trace.
(b)  Derive the condition that must be satisfied for the product of two Hermitian operators to be itself a Hermitian operator.
(c)  Prove that the trace of a matrix operator is invariant under a change of representation, i.e. a change of basis.

Solution:

• Concepts:
  Mathematical foundations of quantum mechanics
• Reasoning:
  This is a linear algebra problem.
• Details of the calculation:
  (a)  ∑_ij|<i|A|j>|² = ∑_ij<i|A|j><j|A^†|i> = ∑_i<i|AA^†|i> = Tr(AA^†), since ∑_j|j><j| = I.
  (b)  Let C = AB, where A and B are Hermitian operators. 
  For any |i>, |j> we have
  <i|AB|j>* = <j|(AB)^†|i> = <j|B^†A^†|i> = <j|BA|i>.
  If C is a Hermitian operator then <i|AB|j>* = <j|AB|i>, or
  <j|BA|i> = <j|AB|i>. for any |i>, |j>.
  C is a Hermitian operator implies that BA = AB, i.e. that A and B commute.
  Let {|u>} be a second orthonormal basis for the state space.E.
  Tr(A) = ∑_i<i|A|i> = ∑_iuu'<i|u><u|A|u'><u'|i> = ∑_iuu'<u'|i><i|u><u|A|u'>
  = ∑_uu'<u'|u><u|A|u'> = ∑_u'<u'|A|u'> = Tr(A),
  since ∑_j|j><j| = ∑_u'|u'><u'| = I.

Problem:

Use the virial theorem for the eigenstates of atomic hydrogen, namely, <nlm|T|nlm> = -E_nl, where E_nl is the eigenenergy of the |nlm> bound state and T is the kinetic energy operator for an electron bound to a proton, to evaluate the sum ∑_nlm|<nlm|p|n'l'm'>|², where p is the momentum operator and the sum is over a complete set of bound and continuum states.  Take the proton mass to be infinite and give your answer in terms of E_n'l' and the mass m_e of the electron.

Solution:

• Concepts:
  Mathematical foundations of quantum mechanics
• Reasoning:
  The eigenvectors of every Hermitian operator form a basis for the vector space,
  ∑_nlm | nlm ><nlm| = 1.
• Details of the calculation:
  ∑_nlm |<nlm|p|n'l'm'>|² = ∑_nlm  <n'l'm'|p^†| nlm><nlm|p|n'l'm'>
  = <n'l'm'|p²|n'l'm'> = 2m_e<n'l'm'|T|n'l'm'> = -2m_eE_n'l'.
  Note: p is a Hermitian operator, p = p^T.

Problem:

Consider the matrix representation of the operator

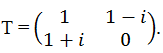
(a)  Is T Hermitian?
(b)  Solve for the eigenvalues.  Are they real?
(c)  Determine the normalized eigenvectors.  Since eigenvectors are not unique to within a phase factor, arrange your eigenvectors so that the first component of each is positive and real.  Are they orthogonal?
(d)  Using the eigenvectors as columns, construct U^†, the inverse of the unitary matrix which diagonalizes T.  Use this to find this diagonalized version T^d = UTU^†.
What is special about the diagonal elements?
(e)  Compare the determinant |T|, the trace Tr(T ), and eigenvalues of T to those of T^d.

Solution:

• Concepts:
  Matrix representation of operators.  (See representations.)
• Reasoning:
  We are given the matrix of an operator in a particular basis. We are asked to find the eigenvalues of the operator and the eigenvectors of the operator in the given basis. We are then asked to make a unitary transformation to a basis in which the matrix of the operator is diagonal.
• Details of the calculation:
  (a)  T_ij = T_ji*,  T is Hermitian.
  (b)  eigenvalues α:  (1 - α )(-α) - 2 = 0.  α₊ = 2,  α_- = -1.  The eigenvalues are real.
  (c)  eigenvector for α₊:
  
  eigenvector for α_-:
  
  The eigenvectors are orthogonal.  <+|-> = <-|+> = 0.
  
  (d)  (See representations.)
  
  
  U^†U = UU^† = I.
  
  The diagonal values now are equal to the eigenvalues.
  
  (e)  det(T) = det(T^d) = -2,  Tr(T) = Tr(T^d) = 1.  Both matrices have the same eigenvalues.

Problem:

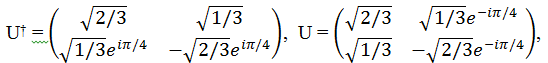
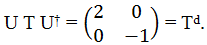
The Hamiltonian operator for a two state system is given by
H = a(|1><1|-|2><2|+|1><2|+|2><1|),
where a is a number with the dimensions of energy.  
(a)  Find the eigenvalues of H and the corresponding eigenkets |ψ₁> and |ψ₂> (as linear combinations of |1> and |2>).
(b)  A unitary transformation maps the {|1>, |2>} basis onto the {|ψ₁>, |ψ₂>} basis.  We have U|i> = |ψ_i>.  Write down the matrix of U and the matrix of U^† in the {|1>, |2>} basis.

Solution:

• Concepts:
  The eigenvalues and eigenvectors of a Hermitian operator.
• Reasoning:
  We are given enough information to construct the matrix of the Hermitian operator H in some basis.  To find the eigenvalues E we set the determinant of the matrix (H - EI) equal to zero and solve for E.  To find the corresponding eigenvectors {|Ψ>}, we substitute each eigenvalue E back into the equation (H  -E*I)|Ψ> = 0 and solve for the expansion coefficients of |Ψ> in the given basis.
• Details of the calculation:
  (a)  In the {|1>, |2>} basis the matrix of H is
  .
  The eigenvalues of H are found from
  
  
  
  For the eigenvectors we find
  
  
  (b)  The matrix of U has the eigenvectors as its columns.
  (See representations.)
  .

Problem:

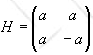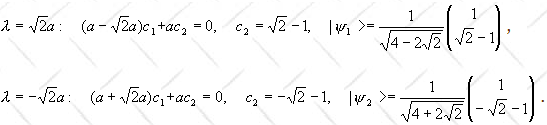
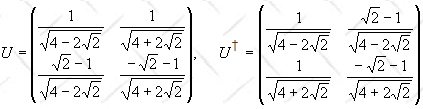Consider a three-state system.  Let {|ω₁>, |ω₂>, |ω₃>} be the non-degenerate orthonormal eigenbasis of the Hermitian operator Ω with |ω₁> having the smallest and |ω₃> the largest eigenvalue.  Let U be the unitary transformation from the {|ω₁>, |ω₂>, |ω₃>} basis to another basis {|t₁>, |t₂>, |t₃>} of the state space.
In the {|t₁>, |t₂>, |t₃>} basis the matrix of the operator Ω is

(a)  Find the eigenvectors Ω in the {|t₁>, |t₂>, |t₃>}.
(b)  Find the matrix U.
(c)  The matrix of another operator M in the {|ω₁>, |ω₂>, |ω₃>} basis is

What is the matrix of M in the {|t₁>, |t₂>, |t₃>} basis?

Solution:

• Concepts:
  Change of representation
• Reasoning:
  |t_i> = ∑_j|ω_j><ω_j|t_i> = ∑_jU_ji|ω_i>.
  The matrix elements of U and U^† are U_ij = <ω_i|t_j>,   U_ij^† = <t_i|ω_j>, respectively.
  The eigenvectors of Ω in the {|t₁>, |t₂>, |t₃>} basis are the columns of the U^† matrix.
• Details of the calculation:
  (a)  The eigenvalues of Ω are λ, where
   

  	-λ	2	0
  	2	-λ	0
  	0	0	1-λ

    = 0.

  
  

  
  λ²(1 - λ) - 4(1 - λ) = 0.  The solutions to this equation are λ₁ = -2, λ₂ = 1, λ₃ = 2.
  The corresponding normalized eigenvectors of Ω in the {|t₁>, |t₂>, |t₃>} basis are

  |1> = 2^-½  

  	-1
  	1
  	0

  ,   |2> =  

  	0
  	0
  	1

  ,   |3> = 2^-½  

  	1
  	1
  	0

  .

  
  

  (b)  (See representations.  Note U and U^† are reversed here.)

  The matrix of U^† is

  U^†  =  

  	-2-½	0	2-½
  	2-½	0	2-½
  	0	1	0

  .  

  
  

  The matrix of U is

  U  =  

  	-2-½	2-½	0
  	0	0	1
  	2-½	2-½	0

  .  

  
  

  The matrix of UΩU^† is diagonal and has the eigenvalues on its diagonal.

  UΩU^† =  

  	-2	0	0
  	0	1	0
  	0	0	2

  .  

  
  

  (c)  An operator is defined by what is does to the basis vectors.
  Let M|A> = |B>.  Let the coordinates of the vector A in the {|ω₁>, |ω₂>, |ω₃>} basis be (a₁, a₂, a₃) and in the {|t₁>, |t₂>, |t₃>} basis be  (a'₁, a'₂, a'₃).
  We have a'_i = <t_i|A> =  ∑_j<t_i|ω_j><ω_j|A>  = ∑_jU^†_ija_j.

  Let the coordinates of the vector B in the {|ω₁>, |ω₂>, |ω₃>} basis be (b₁, b₂, b₃).
  Its coordinates in the {|t₁>, |t₂>, |t₃>} basis are b'_i =  ∑_jU^†_ijb_j.
  M|A> = |B> --> b_j = ∑_kM_jk|a_k> or b'_j = ∑_kM'_jk|a'_k>.
  b'_i =  ∑_jU^†_ijb_j = ∑_jkU^†_ijM_jl|a_l> = ∑_jklU^†_ijM_jlU_lk|a'_k>.
  Therefore M'_jl =  ∑_jlU^†_ijM_jlU_lk,  or  M' =  U^†MU.
  We therefore have M' = U^†MU.

  M' =  

  	0	-i	0
  	i	0	0
  	0	0	i

  .