Photons, deBroglie wavelength, electron diffraction

Photons

Problem:

A pulsed ruby laser emits light having a wavelength of 694.3 nm.  For a 14 ps pulse containing 3.0 J of energy, find
(a)  the physical length of the pulse as it travels through space.
(b)  the number of photons in it.

Solution:

• Concepts:
  Speed of light, photon energy
• Reasoning:
  The energy is transported by photons, which move with the speed of light.
• Details of the calculation:
  (a)  Length of pulse L = 3*10⁸ m/s * 14 ps = 4.2 mm.
  (b)  Number of photons = 3 J/(energy per photon)
  Photon energy = hc/λ = 2.86*10^-19 J.
  Number of photons = 10¹⁹.

Problem:

Calculate the long-wavelength limit of the sensitivity of a photocathode layer with work function of 1.5  eV.

Solution:

• Concepts:
  The photoelectric effect, the cutoff frequency
• Reasoning:
  A photon with the cutoff frequency f_c has just enough energy to eject an electron.
  hf_c = Φ, Φ = work function.
• Details of the calculation:
  hf_c = hc/λ_c = f,  λ_c =  hc/f = 1240 eV nm/(1.5 eV) = 827 nm.

Problem:

Photons of energy 0.2 MeV are being scattered by a free electrons (initially at rest).
(a)  At what angle must the scattering occur so that photons lose 10% of its energy?
(b)  What is the momentum of corresponding electrons after scattering?

Given:  Δλ = (λ_f - λ_i) = [h/(m_ec)](1 - cosθ) for Compton scattering.

Solution:

• Concepts:
  Wavelength, momentum, and energy of photons
• Reasoning:
  λ = h/p = hc/E
  The Compton formula is given, we do not have to derive it.
• Details of the calculation:
  (a)  The initial energy of the photons is E_i = 0.2 MeV and their wavelength is λ_i = hc/E_i =0.0062 nm.
  After the collision the photons lose 10% of their energy, thus their final kinetic energy is E_f = 0.18 MeV and their wavelength is λ_f = hc/E_f = 0.0069 nm.
  Δλ = λ_f - λ_i = 0.0007 nm.
  Δλ = (λ_f - λ_i) = λ_c(1 - cosθ), λ_c  = h/(m_ec) = 2.426*10^-12 m.
  θ = cos^-1([λ_i - λ_f + λ_c)/λ_c] = 44.6^o.
  (b)  Assume the photons are incident along the x-axis.
  
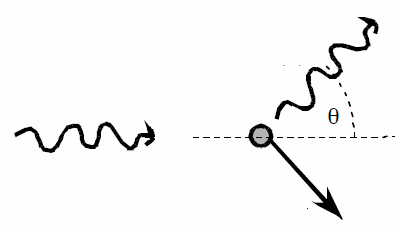
  Given the photon wavelength and the scattering angle, we find the x- and y-component of the momentum of the scattered photon.
  The total momentum must be conserved, so we can solve for the momentum of the scattered electron.
  For the photon before the collision:  p_x = h/λ_i, p_y = 0.
  For the photon after the collision:  p_x = (h/λ_f)cosθ,  p_y = (h/λ_f)sinθ.
  Momentum conservation:
  For the scattered electron:  p_x =  h/λ_i - (h/λ_f)cosθ = 3.85*10^-23 kg m/s.
  p_y = -(h/λ_f)sinθ = 6.74*10^-23 kg m/s.
  p = (p_x² + py²)^½ = 7.76*10^-23 kg m/s.

deBroglie wavelength

Problem:

N indistinguishable particles of mass m are confined to a box of volume V.  The temperature of this gas is T.
(a)  Above what temperature do you expect relativistic effects to become important?
(b)  Below which temperature do you expect quantum mechanical effects to become important?

Solution:

• Concepts:
  Limitations of Newtonian Physics
• Reasoning
  Even in large systems quantum mechanical effects can become observable in a system of indistinguishable particles.
• Details of the calculation:
  (a)  We expect relativistic effects to become when kT ~ mc², T ~ mc²/k.
  (b)  We expect quantum mechanical effects to become important when the particles become indistinguishable for practical purposes, i.e. when their wave packets start overlapping.  This happens when the average spacing between the particles becomes comparable to their deBroglie wavelength.
  deBroglie wavelength:  λ = h/p = (h²/p²)^½ ~  (h²/(2mkT))^½.
  Average spacing between the particles: d ~ (V/N)^(1/3).
  Therefore (h²/(2mkT))^½ ~ (V/N)^(1/3),  T ~ (h²/(2m))(V/N)²

Problem:

Compute the speed and the deBroglie wavelength of
(a)  an electron whose kinetic energy is 5 eV.
(b)  an electron whose kinetic energy is 5 MeV.
(c)  a proton whose kinetic energy is 5 MeV.
(d)  a baseball ( m = 150 g) whose kinetic energy is 5 MeV.

Solution:

• Concepts:
  The deBroglie wavelength
• Reasoning:
  We are asked to find the deBroglie wavelength of various objects.
  λ = h/p.  We need to decide if we must use the relativistically correct expression for p, or if the non-relativistic expression suffices.
• Details of the calculation:
  (a)  non-relativistic: T = 5 eV = p²/(2m).
  λ = h/(2m_e 5 eV)^½ = hc/(2m_ec² 5 eV)^½
  = 1.24*10⁴ eV-Å/(10*0.51*10⁶ eV²)^½ = 5.5 Å.
  (b)  relativistic:  E = m_ec² + T.  E² = m_e²c⁴ + 2Tm_ec² + T².
  E² = p²c² + m_e²c⁴,  p²c² = 2Tm_ec² + T².
  λ = hc/(2Tm_ec² + T²)^½
  = 1.24*10⁴ eV-Å/(((5*10⁶)² + 2*5*10⁶*0.511*10⁶) eV²)^½ =  2.3*10^-3 Å.
  (c)  non-relativistic: T = 5 MeV = p²/(2m).
  λ = h/(2m_p 5 MeV)^½ = hc/(2m_pc² 5*10⁶ eV)^½
  = 1.24*10⁴ eV-Å/(10*10⁶*938*10⁶ eV²)^½ =  1.28*10^-4 Å.
  (d)  non-relativistic: T = 5 MeV =  8*10^-13 J = p²/(2m).
  λ = h/(2m_b T)^½ = 6.626*10^-34 Js/(2*0.15 kg 8*10¹³ eV)^½ = 1.35*10^-27 m = 1.35*10^-17 Å.

Problem:

Consider thermal neutrons in equilibrium at temperature T = 300 K.
(a)  Calculate its deBroglie wavelength.  State whether a beam of these neutrons could be diffracted by a crystal, and why?
(b)  Use Heisenberg's uncertainty principle to estimate the kinetic energy (in MeV) of a nucleon bound within a nucleus of radius 10⁻¹⁵ m.

Solution:

• Concepts:
  The deBroglie wavelength, the uncertainty principle
• Reasoning:
  Matter waves lead to the uncertainty principle.
• Details of the calculation:
  (a)  The absolute temperature T of a collection of particles in equilibrium is proportional to the average translational kinetic energy of the particles. 
  ½m<v²> = <p²>/(2m) = (3/2)k_BT.
  p_rms = (3mk_BT)^½,  p_rmscc = (3mc²k_BT)^½ = (3*940*10⁶ eV*8.617*10^-5 eV/K * 300 K)^½.
  p_rmsc = 8538 eV.
  λ = h/p = hc/pc = (1240 eV nm)/(8538 eV) = 0.145 nm.
  Such neutrons can be diffracted by crystals as their deBroglie wavelength is comparable with the inter-atomic distance in the crystal.
  (b)  If the neutron is confined, the uncertainty in any Cartesian momentum component is on the order of the magnitude of the momentum.
  ∆p_x∆x ~ ħ, set ∆p_x = p.  pc = ħc/∆x = (1240 eV nm)/(2π*10⁻⁶ nm) = 197.3 MeV.
  E = (p²c² + m²c⁴)^½ = ((197.3 MeV)² + (940 MeV)²)^½ = 960.5 MeV.
  T = E - mc² = 20.5 MeV.

Problem:

(a)  Show that the deBroglie wavelength of a particle approaches zero faster than 1/v as its speed v approaches the speed of light.
(b)  Find the deBroglie wavelength of a 15 eV proton.
(c)  Find the deBroglie wavelength of a 15 keV electron.
(d)  What is the deBroglie wavelength of an electron whose speed is 9*10⁷ m/s?
(e)  Find the wavelength of a 1 kg object whose speed is 1 m/s.
(f)  Neutrons in equilibrium with matter at room temperature (300 K) have average energy of about ½5 eV.  Such neutrons are often called "thermal" neutrons.  Find their deBroglie wavelength.
(g)  Derive a formula expressing the deBroglie wavelength (in Å) of an electron in terms of the potential difference U (in Volts) through which it is accelerated.
(h)  Derive a formula for the deBroglie wavelength of a particle in terms of its kinetic energy T and its rest energy mc².

Solution:

• Concepts:
  The deBroglie wavelength
• Reasoning:
  We are asked to find the deBroglie wavelength of various objects.
• Details of the calculation:
  (a)  λ = h/p = h/(γmv), 1/(γv) = (1 - v²/c²)^½/v
  = (1/v² - 1/c²)^½ < 1/v for v < c.
  (b)  non-relativistic: T = 15 eV = p²/(2m).
  λ = h/(2m_p 15 eV)^½ = hc/(2m_pc² 15 eV)^½
  = 1.24*10⁴ eV-Å/(30*938*10⁶ eV²)^½ = 7.4*10^-2 Å.
  (c)  non-relativistic: T = 15 keV = p²/(2m).
  λ = h/(2m_e 15 keV)^½ = hc/(2m_ec² 15*10³ eV)^½
  = 1.24*10⁴ eV-Å/(30*10³*0.511*10⁶ eV²)^½ = 0.1 Å.
  relativistic:  E = m_ec² + T.  E² = m_e²c⁴ + 2Tm_ec² + T².
  E² = p²c² + m_e²c⁴,  p²c² = 2Tm_ec² + T².
  λ = hc/(2Tm_ec² + T²)^½
  = 1.24*10⁴ eV-Å/(((15*10³)² + 2*15*10³*0.511*10⁶)² eV²)^½ =  0.1 Å.
  (d)  relativistic:  λ = h/(γmv) = hc²(1 - v²/c²)^½ /(m_ec²v).
  = 1.24*10⁴ eV-Å*(1 - 9*10^-2)^½*3*10⁸/(0.511*10⁶ eV*9*10⁷ m/s) = 7.7*10^-2 Å.
  (e) non-relativistic:  λ = h/(mv) = 6.626810^-34 Js/(1 kg*1 m/s) = 6.626810^-34 m.
  (f)  non-relativistic:  λ = h/(2m_nE)^½
  = 1.24*10⁴ eV-Å/(2*939.57*10⁶/25 eV²)^½ = 1.4 Å.
  (g)  T = U eV.
  non-relativistic: λ = hc/(2m_ec² U eV²))^½ = 12.27/(U)^½ Å.
  relativistic:  λ = hc/(2Um_ec² + U)²)^½ = 1.24*10⁴/(2*0.511*10⁶* U + U²)^½ Å.
  (h)  λ = hc/(2Tm_ec² + T²)^½.

Electron diffraction

Problem:

If we send electrons with energy of 25 eV through the same two slits (d = 0.5 mm) we use to produce a visible light interference pattern, what is the spacing between maxima on a screen 3 m away?

Solution:

• Concepts:
  Electron diffraction
• Reasoning:
  The wavelength of the electrons is λ = h/p = h/(2mE)^½.
• Details of the calculation:
  λ = [6.62*10^-34/(2*9.1*10^-31*25*1.6*10^-19)^½] m = 2.45*10^-10 m.
  d*sin θ = nλ, set n = 1.  sin θ ~z/L.  d = 5*10^-4 m.
  5*10^-4 z/3 = 2.45*10^-10 m.  z = 1.47*10^-6 m.

Problem:

Consider a crystal with the atoms arranged in cubic array, each atom at distance 0.91 Å from its nearest neighbor.
Examine the conditions for Bragg reflection from atomic planes connecting diagonally placed atoms.

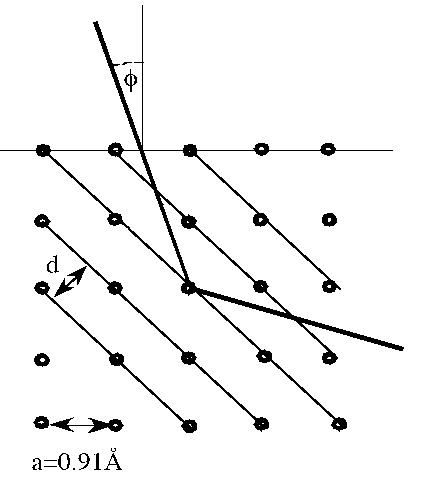
(a)  Find the lowest energy of electrons that can produce a first order maximum.
(b)  If 300 eV electrons are used, at what angle from the crystal normal must they be incident to produce a first order maximum?

Solution:

• Concepts:
  Bragg reflection
• Reasoning:
  In Bragg reflection the condition for constructive interference is: nλ = 2d sinθ, where θ is the angle between the incident wave vector and the scattering planes.
  
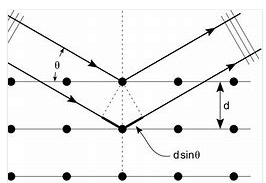
• Details of the calculation:
  (a)  The largest angle θ for which a reflection can occur is θ = 90^o. 
  The longest wavelength for first-order reflection therefore is λ = 2d sinθ = 2(a sin45^o)sin90^o = 2(0.91Å * 0.71) = 1.29 Å.
  This is the wavelength of the lowest energy electrons.
  Using de Broglie formula we can find the corresponding energy of electrons.
  E = p²/2m = (h/λ)²/2m = 1.45 *10^-17 J = 90.4 eV
  (b)  The wavelength of the 300 eV electrons is λ = h/p = h/(2mE)^½ = 7*10^-11 m.
  For first-order Bragg reflection we therefore have
  θ = sin^-1(λ/2d) = sin^-1(λ/2asin45^o) = sin^-1(0.55) = 33.38^o.
  Since the angle of from the normal to crystal surface φ = 45^o - θ , first order reflection will occur for φ = 45^o - 33.38^o = 11.62^o.