Probability density, probabilities,  and the mean value of an observable

Probability density

Problem:

A particle confined in the region [−a, +a] has a wave function ψ(x) = N(a² − x²).  What is the probability that a position measurement would find it located in the interval [−a/2, +a/2]?

Solution:

• Concepts:
  The fundamental assumptions of quantum mechanics
• Reasoning:
  The wave function ψ(r,t) is interpreted as a probability amplitude of the particles presence.  |ψ(r,t)|² is the probability density. 
• Details of the calculation:
  Normalize the wave function:  ∫_-a^a(a² − x²)²dx = 2∫₀^a (a² − x²)²dx = 16a⁵/15.
  N² = 15/(16a⁵).
  P[−a/2, +a/2] = 30/(16a⁵)∫₀^a/2 (a² − x²)²dx = 0.793. 

Probabilities

Problem:

A quantum system can exist in two states |a₁> and |a₂>, which are normalized eigenstates of the observable A with eigenvalues 0 and 1.  A second observable B is defined by B|a₁> = 7|a₁> - 24i|a₂>,  B|a₂> = 24i|a₁> - 7|a₂>.
(a)  Find the eigenstates of B.
(b)  The system is in the state |a₁> when B is measured.  Immediately afterwards A is measured.  Find the probability that a measurement of A gives the result 0.

Solution:

• Concepts:
  The postulates of Quantum Mechanics
• Reasoning:
  When a physical quantity described by the operator A is measured on a system in a normalized state |ψ>, the probability of measuring the eigenvalue a_n is given by
  P(a_n) = Σ_i=0^gn|<u_nⁱ|ψ>|²,  where {|u_nⁱ>} (i=1,2,...,g_n) is an orthonormal basis in the eigensubspace E_n associated with the eigenvalue a_n.
  If a measurement on a system in the state |ψ> gives the result a_n, then the state of the system immediately after the measurement is the normalized projection of |ψ> onto the eigensubspace associated with a_n.
• Details of the calculation:
  B_ij = <a_i|B|a_j>b)(-7 -b)
  B₁₁ = 7,  B₁₂ = 24i, 
  B₂₁ = -24i,  B₂₂ = -7.
  det(B - bI) = 0,   (7 - b)(-7 - b) - 24² = 0, b = ±25.

  b₁ = +25:  (7 - 25)c₁ + 24i c₂ = 0,  c₂ = -i¾c₁, 
  |c₁|² + |c₂|² = 1,  c₁ = 4/5,  c₂ = -i3/5.
  |b₁> = (4/5)|a₁> - i(3/5)|a₂>.

  b₂ = -25:  (7 + 25)c₁ + 24i c₂ = 0,  c₂ = i(4/3)c₁, 
  |c₁|² + |c₂|² = 1,  c₁ = 3/5,  c₂ = i4/5.
  |b₂> = (3/5)|a₁> + i(4/5)|a₂>.

  (b)  There are two paths.
  (i)  Measure b₁, then measure a₁ = 0.
  P_a1(b1) = |<b₁|a₁>|² = (4/5)².  P_b1(a1) = |<a₁|b₁>|² = (4/5)².
  P_a1(a₁ after b₁) = (4/5)⁴.
  (ii)  Measure b₂, then measure a₁ = 0.
  P_a1(b₂) = |<b₂|a₁>|² = (3/5)².  P_b2(a1) = |<a₁|b₂>|² = (3/5)².
  P_a1(a₁ after b₂) = (3/5)⁴.
  P_a1(a₁ after measurement of B) = (4/5)⁴  + (3/5)⁴ = 337/625 = 0.54.

Problem:

Let A and B be two observables of a system with a two dimensional state space, and suppose measurements are made of A, B, and A again in quick succession.
Show that the probability that the second measurement of A gives the same result as the first is independent of the initial state of the system.

Hint:
Let {|a₁>,|a₂> } be an othonormal eigenbasis of A and let {|b₁>,|b₂> } be an othonormal eigenbasis of B.
A|a_i> = a_i|a_i>,  B|b_i> = b_i|b_i>.
|b₁> = cos(θ)|a₁> + sin(θ)e^iφ|a₂>,  |b₂> = -sin(θ)|a₁> + cos(θ)e^iφ|a₂>
is the most general expansion of the |b_i> in terms of the |a_i>.
<b₁|b₂> = 0,  <b₁|b₁> = <b₂|b₂> = 1.
The initial state can be written as some linear combination of |a₁> and a₂>.
|Ψ> = c₁|a₁> + c₂|a₂>.

Solution:

• Concepts:
  Fundamental assumptions of QM
• Reasoning:
  When a physical quantity described by the operator A is measured on a system in a normalized state |Ψ>, the probability of measuring the eigenvalue a_n is given by
  P(a_n) = ∑_i=0^gn|<u_nⁱ|Ψ>|²,  where {|u_nⁱ>} (i=1,2,...,g_n) is an orthonormal basis in the eigensubspace Ε_n associated with the eigenvalue a_n.
• Details of the calculation:
  The initial state can be written as some linear combination of |a₁> and a₂>.
  |Ψ> = c₁|a₁> + c₂|a₂>,  |c₁|² + |c₂|² = 1 for a normalized state.
  Branch 1:
  Assume the first measurement yields a₁.  The probability for this outcome is |c₁|².
  What is the probability of measuring a₁ again after a measurement of B?
  P_a1(b₁) = cos²(θ) (system is now in state |b₁>), P_b1(a₁) = cos²(θ),
  P_a1(b₁) P_b1(a₁)  = cos⁴(θ),
  P_a1(b₂) = sin²(θ) (system is now in state |b₂>), P_b2(a₁) = sin²(θ),
  P_a1(b₂) P_b2(a₁)  = sin⁴(θ).
  Probability of the first path + probability of the second path = cos⁴(θ) + sin⁴(θ).
  Total probability for this branch:  |c₁|²(cos⁴(θ) + sin⁴(θ)).

  Branch 2:
  Assume the first measurement yields a₂.  The probability for this outcome is |c₂|².
  What is the probability of measuring a₂ again after a measurement of B?
  P_a2(b₁) = sin²(θ) (system is now in state |b₁>), P_b1(a₂) = sin²(θ),
  P_a2(b₁) P_b1(a₂)  = sin⁴(θ),
  P_a2(b₂) = cos²(θ) (system is now in state |b₂>), P_b2(a₂) = cos²(θ),
  P_a2(b₂) P_b2(a₂)  = cos⁴(θ).
  Probability of the first path + probability of the second path = sin⁴(θ) + cos⁴(θ).
  Total probability for this branch:  |c₂|²(cos⁴(θ) + sin⁴(θ)).
  Probability of obtaining the same result =  (|c₁|² + |c₂|²)(cos⁴(θ) + sin⁴(θ))
  = cos⁴(θ) + sin⁴(θ), independent of the initial state.

Mean value of an observable

Problem:

The wave function ψ of a particle is written as a linear combination of the three orthonormal eigenfunctions {Φ_i} of the observable A with eigenvalues a_i (i = 1,2,3).
|ψ> = (1/√6)|Φ₁> + (1/√3 )|Φ₂> + (1/√2) |Φ₃>
Find <A>.  What is the probability that the measurement of A yields a₂?   Find the wave function immediately after this measurement.

• Concepts:
  The postulates of Quantum Mechanics, the mean value
• Reasoning:
  The expression for the mean value of an observable A in the normalized state |ψ> is <A> = <ψ|A|ψ>.
  When a physical quantity described by the operator A is measured on a system in a normalized state |ψ>, the probability of measuring the eigenvalue a_n is given by
  P(a_n) = Σ_i=0^gn|<u_nⁱ|ψ>|²,  where {|u_nⁱ>} (i=1,2,...,g_n) is an orthonormal basis in the eigensubspace E_n associated with the eigenvalue a_n.
  If a measurement on a system in the state |ψ> gives the result a_n, then the state of the system immediately after the measurement is the normalized projection of |ψ> onto the eigensubspace associated with a_n.
• Details of the calculation:
  <ψ|ψ> = 1/6 + (1/3) + ½ = 1.  |ψ> is normalized.
  <A> = <ψ|A|ψ> = a₁/6 + a₂/3 + a₃/2.
  The probability that a measurement will yield a₂ is |<Φ₂|ψ>|² = (1/3).
  Immediately after the measurement the wave function is Φ₂.

Problem:

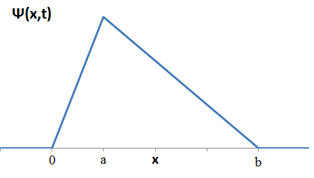
At some time t the wave function of a particle is a triangular hat wave function given by
Ψ(x,t) = Ax/a                       for 0 < x < a,
Ψ(x,t) = A(b - x)/(b - a)        for a < x < b,
Ψ(x,t) = 0                            otherwise,
where A, a, and b are constants.
(a)  Sketch Ψ and find the most probable location of the particle at time t.
(b)  Determine the normalization constant A in terms of a and b.
(c)  At time t, what are the probabilities of the particle being found left and right of a, respectively?
(d)  What is <x(t)>?

Solution:

• Concepts:
  Probability density |Ψ(x,t) |²
• Reasoning:
  We are given a wave function and asked to normalize it and find probabilities.
• Details of the calculation:
  (a)  The most probable location is at x = a where Ψ(x,t) and therefore |Ψ(x,t) |² has its maximum value.

  
  
  (b)  ∫|Ψ(x,t)|²dx = 1,  (A/a)²∫₀^ax² dx  + [A²/(b - a)²]∫_a^b(b - x)² dx = 1.
  A²b/3 = 1,  A² = 3/b.
  (c)  P(left of a) = a/b.
  P(right of a) = 1 - a/b.
  If b = 2a then P(left of a) = P(right of a) = ½.
  (d)  <x> = ∫x|Ψ(x,t)|²dx  = (A/a)²∫₀^ax³ dx  + [A²/(b - a)²]∫_a^b(b - x)² x dx.
  <x> = ¼(b + 2a).
  If b = 2a then <x> = a.

Problem:

Assume the wave function of a particle is Ψ(x) = N exp(ip₀x/ħ)/(x² + a²)^½.
Here a and p₀ are real constants and N is a normalization constant.
(a)  Find N so that ψ(x) is normalized.
(b)  If the position of the particle is measured, what is the probability of finding the particle between  -a/√3  and  +a/√3?
(c)  Calculate the mean value of the momentum of the particle. 

• Concepts:
  The postulates of Quantum Mechanics, the mean value
• Reasoning:
  When a physical quantity described by the operator A is measured on a system in a normalized state |ψ>, the probability of measuring the eigenvalue a_α is given by dP(a_α) = |<u_α|ψ>|²dα, where |u_α> is the eigenvector corresponding to the eigenvalue a_α; we assume a_α is a non-degenerate continuous eigenvalue of A.
  The expression for the mean value of an observable A in the normalized state |ψ> is <A> = <ψ|A|ψ>. 
• Details of the calculation:
  (a) <Ψ|Ψ> = 1.  ∫_-∞^+∞Ψ*(x)Ψ(x) dx = 1.
  N²∫_-∞^+∞exp(-ip₀x/ħ)/(x² + a²)^½ exp(ip₀x/ħ)/(x² + a²)^½
  = N²∫_-∞^+∞dx/(x² + a²)  = 1.
  ∫_-∞^+∞dx/(x² + a²)  = (1/a)tan^-1(x/a)|_-∞^+∞  = (1/a)[π/2 - (-π/2)] = π/a.
  N² = a/π,  N = (a/π)^½.

  (b)  Let P denote the probability of finding the particle between -a/√3 and +a/√3.
  Let y = a/√3.
  P = ∫_-y^+y |Ψ(x)|² dx = (a/π)∫_-y^+ydx/(x² + a²)  = (1/π)tan^-1(x/a)|_-y^+y

  = (1/π)[tan^-1(1/√3) - tan^-1(-1/√3)]
  = (1/π)[π/6 + π/6] = (1/3).

  (c)  Let <P> denote the mean value of the momentum of the particle. 
  <P> = ∫_-∞^+∞Ψ*(x) ((ħ/i)∂/∂x) Ψ(x) dx
  = (a/π)∫_-∞^+∞exp(-ip₀x/ħ)/(x² + a²)^½ (ħ/i)[(ip₀/ħ)exp(ip₀x/ħ)/(x² + a²)^½ - x exp(-ip₀x/ħ)/(x² + a²)^3/2]
  = (a/π)p₀∫_-∞^+∞dx/(x² + a²)  - (a/π)(ħ/i)∫_-∞^+∞ xdx/(x² + a²)² = p₀.
                        (π/a)                                 0, odd function

Problem:

From measurements of the differential cross section for scattering of electrons off protons (in atomic hydrogen) it was found that the proton had a charge density given by ρ(r) = αexp(-βr) where α and β are constants.
(a)  Find α and β such that the proton charge equals e, the charge on the electron.
(b)  Show that the protons mean square radius <r²> is 12/β².
(c)  Assuming a reasonable value for <r²>^½ calculate a in esu/cm³.

Solution:

• Concepts:
  Fundamental assumptions of Quantum Mechanics
• Reasoning:
  We interpret |ψ(r)|² as the probability density and assume that the probability density is proportional to the charge density.  We then normalize the wave function ψ(r) and find the average value of the observable r².
• Details of the calculation:
  (a)  4π∫₀^∞ρ(r)r²dr = α4π∫₀^∞exp(-βr)r²dr = (α/β³)4π∫₀^∞exp(-r')r'²dr' = (α/β³)8π = e.
  (b)  Assume ρ(r) = A²|ψ(r)|². 
  For a normalized wave function 4π∫₀^∞|ψ(r)|²r²dr = 1.
  Therefore A² = β³/(8πα),  |ψ(r)|² = [β³/(8π)]exp(-βr)
  <r²> = 4π∫₀^∞|ψ(r)|²r⁴dr = [β³/2]∫₀^∞exp(-βr)r⁴dr = (1/(2β²))∫₀^∞exp(-r')r'⁴dr'
  = 4!/(2β²) = 12/β².
  (c)  Assume <r²>^½ = 10^-15 m = 10^-13 cm.
  Then β² = 12/<r²> = 1.2*10²⁷ cm^-2.
  (α/β³)8π = 4.8*10^-10 esu,  α = 7.9*10²⁹ esu cm^-3.