Delta function potentials
Problem:
A one-dimensional potential well is given in the form of a delta function at x =
0,
U(x) = Cδ(x), C < 0. A stream of non-relativistic particles of
mass m and energy E approaches the origin from one side.
(a) Derive an expression
for the reflectance R(E).
(b) Can you express R(E) in terms of sin2(δ), where δ is the
phase shift of the transmitted wave?
Solution:
- Concepts:
This is a "square potential" problem. We solve HΦ(x)
= EΦ(x) in regions where V(x) is constant and apply
boundary conditions.
- Reasoning:
U(x) = 0 everywhere except at x = 0.
- Details of the calculation:
(a)
Φ1(x) = A1 exp(ikx) + A1'exp(-ikx) for
x < 0. k2 = 2mE/ħ2.
Φ2(x) = A2 exp(ikx) for
x > 0.
Φ is continuous at x = 0. Φ1(0)
= Φ2(0). A1 + A1'
= A2.
∂2Φ(x)/∂x2
+ (2m(E - U(x))/ħ2)Φ(x) =
0.
Let us evaluate this equation at x = ε and at x = -ε
and write down a difference equation.
∂Φε(x1 + ε)/∂x
- ∂Φε(x1 - ε)/∂x
= (2m/ħ2)∫x1-εx1+ε (Cδ(x) - E) Φ(x) dx
= (2mC/ħ2)Φ(0).
If U does not remain finite at the step, then ∂Φ/∂x has a finite
discontinuity at the step.
iA1k - iA1'k = iA2k - A22mC/ħ2,
A1 - A1' = A2 - A22mC/(ikħ2)
= [1 - 2mC/(ikħ2)]A2.
Eliminate A1':
2A1 = [2 - 2mC/(ikħ2)]A2, A1 = [1
+ imC/(kħ2)]A2,
T(E) = (k|A2|2)/(k|A1|2) = ħ4k2/(ħ4k2
+ m2C2) = E/(E + mC2/(2ħ2)).
R(E) = 1 - T(E) = [mC2/(2ħ2)]/(E + mC2/(2ħ2))
= m2C2/(ħ4k2
+ m2C2).
(b) A2 = A1/ [1 + imC/(kħ2)] = A1(1
- imC/(kħ2))/[1 + m2C2/(k2ħ4)]
= |A1|exp(iδ).
tanδ = -mC/(kħ2).
sinδ = [-mC/(kħ2)]/[1 + m2C2/(k2ħ4)]1/2.
sin2δ = [m2C2/(k2ħ4)]/[1
+ m2C2/(k2ħ4)] = R(E).
Problem:
A one-dimensional potential well is given in the form of a delta function at x =
0,
U(x) = Cδ(x), C < 0.
(a) A non-relativistic particle of mass m and energy E is incident from one
side of the well.
Derive an expression for the coefficient of transmission T(E).
(b) Since a bound state can exist with the attractive potential, find the
binding energy of the ground state of the system.
Solution:
- Concepts:
This is a "square potential" problem. We solve HΦ(x)
= EΦ(x) in regions where U(x) is constant and apply
boundary conditions.
- Reasoning:
U(x) = 0 everywhere except at x = 0.
- Details of the calculation:
(a) E > 0.
Φ1(x) = A1 exp(ikx) + A1'exp(-ikx) for
x < 0. k2 = 2mE/ħ2.
Φ2(x) = A2 exp(ikx) for
x > 0.
Φ is continuous at x = 0. Φ1(0)
= Φ2(0). A1 + A1'
= A2.
∂Φ/∂x has a finite discontinuity at x = 0.
∂2Φ(x)/∂x2
+ (2m(E - U)/ħ2)Φ(x) = 0.
Let us evaluate this equation at x = ε and at x = -ε
and write down a difference equation.
∂Φ2ε(x1 + ε)/∂x
- ∂Φ1ε(x1 - ε)/∂x
= -(2m/ħ2)∫x1-εx1+ε (E - Cδ(x)) Φ(x) dx
= (2mC/ħ2)Φ(0).
iA1k - iA1'k = iA2k - A22mC/ħ2,
A1 - A1' = A2 - A22mC/(ikħ2)
= [1 - 2mC/(ikħ2)]A2.
Eliminate A1':
2A1 = [2 - 2mC/(ikħ2) ]A2, A2/A1
= 1/[1 - mC/(ikħ2)] = ikħ2/(ikħ2
- mC).
T(E) = (k|A2|2)/(k|A1|2) = ħ4k2/(ħ4k2
+ m2C2) = E/(E + mC2/(2ħ2)).
(b) E < 0.
Φ1(x) = A1 exp(ρx)
+ A1'exp(-ρx) for x < 0.
ρ2 = -2mE/ħ2.
Φ2(x) = A2 exp(ρx)
+ A2'exp(-ρx) for x > 0.
Φ is finite at infinity.
If we choose ρ > 0, then A1' = A2 = 0. Φ is continuous
at x = 0. Φ1(0) = Φ2(0). A1
= A2' = A.
∂Φ2/∂x|x=ε =
∂Φ1/∂x|x=-ε + (2mC/ħ2)Φ(0),
as ε --> 0
-ρA - (2mC/ħ2)A = ρA, ρ = -mC/ħ2.
m2C2/ħ4 = -2mE/ħ2, E
= -mC2/(2ħ2).
Only one bound state exists.
Problem:
Consider the non-relativistic motion in one dimension of a particle outside an
infinite barrier at x ≤ 0 with an additional delta
function potential at x = a, i.e. U(x) = ∞ for
x ≤ 0, U(x) = Fδ(x - a)
for x > 0, where F is a positive constant. Derive an analytical expression
for the phase shift δ(k) for a particle approaching
the origin from x = +∞ with momentum ħk.
Solution:
- Concepts:
This is a "square potential" problem. We solve HΦ(x)
= EΦ(x) in regions where U(x) is constant and apply
boundary conditions.
- Reasoning:
U(x) = 0 for x > 0 except at x = a. U(x) = ∞ for
x ≤ 0.
- Details of the calculation:
The most general solution of the" time-independent" Schroedinger
equation in region 1 is Φ1(x) = A sin(kx)
because Φ1(x) = 0 due to the boundary
condition at x = 0.
The most general solution in region 2 is
Φ2(x) = B sin(kx + δ(k)).
The boundary conditions at x = a are
Φ1(a) =
Φ2(a),
∂Φ1/∂x|a = ∂Φ2/∂x|a
- (2mF/ħ2)Φ(a).
A sin(ka) = B sin(ka + δ(k)), kA cos(ka) = kB cos(ka + δ(k))
- (2mF/ħ2)A sin(ka).
cot(ka) + (2mF/ħ2) = cot(ka + δ(k)),
δ(k) = cot-1(cot(ka) + (2mF/ħ2)) - ka.
Problem:
Consider the scattering of a particle of mass m and total
energy E = ħ2k2/(2m) under the influence of a
localized one-dimensional potential.
(a) Let the potential be a delta function potential well, U(x) = -aU0δ(x)
with a > 0 and U0 = ħ2k02/(2m).
What are the asymptotic boundary conditions at x = ∞
and the matching conditions at x = 0 for
the wave function?
(b) Define the transmission coefficient T and the
reflection coefficient R and find the relationship between T and R.
(c) How does the transmission coefficient depend on E?
(d) Now the potential is replaced by a double delta function
potential well. The delta functions are a distance b apart, i.e.
U(x) = -aU0δ(x) - aU0δ(x - b).
By inspecting the matching conditions without
solving the algebra equation, explain intuitively the limiting behavior of the
transmission coefficient T for E --> 0 and
E --> ∞.
Solution:
- Concepts:
This is a "square potential" problem. We solve HΦ(x)
= EΦ(x) in regions where U(x) is constant and apply
boundary conditions.
- Reasoning:
U(x) = 0 everywhere except at x = 0 (and x = b in part d).
- Details of the calculation:
(a) Φ is continuous at x = 0. ∂Φ/∂x has a finite
discontinuity at x = 0.
Assume the particle is incident from the left.
Φ1(x) = A1 exp(ikx) + A1'exp(-ikx) for
x < 0. k2 = 2mE/ħ2.
Φ2(x) = A2 exp(ikx) for
x > 0.
(b)
Φ is continuous at x = 0. Φ1(0)
= Φ2(0). A1 + A1'
= A2.
∂Φ/∂x has a finite discontinuity at x = 0.
∂2Φ(x)/∂x2
+ (2m(E - U)/ħ2)Φ(x) = 0.
Let us evaluate this equation at x = ε and at x = -ε
and write down a difference equation.
∂Φε(ε)/∂x
+ ∂Φε(-ε)/∂x
= -(2m/ħ2)∫-ε+ε (-aU0δ(x) - E) Φ(x) dx
= (2maU0/ħ2)Φ(0).
iA1k - iA1'k = iA2k - A22maU0/ħ2,
A1 - A1' = A2 - A22maU0/(ikħ2)
= [1 - 2maU0/(ikħ2)]A2.
Eliminate A1':
2A1 = [2 - 2maU0/(ikħ2) ]A2, A2/A1
= 1/[1 - maU0/(ikħ2)] = ikħ2/(ikħ2
- maU0).
T(E) = (k|A2|2)/(k|A1|2) = ħ4k2/(ħ4k2
+ m2a2U02) = E/(E + ma2U02/(2ħ2)).
Eliminate A2:
A1 - A1' = A2 - A22maU0/(ikħ2)
= [1 - 2maU0/(ikħ2)](A1 + A1').
A1'/A1
= 2maU0/(ikħ2)/ [2 - 2maU0/(ikħ2)]
= -maU0/(ikħ2 - maU0).
R(E) = (k|A1'|2)/(k|A1|2) =
ma2U02/(ħ4k2
+ m2a2U02).
T + R = 1
(c)
T(E) = E/(E + ma2U02/(2ħ2)).
As E --> 0, T --> 0, R --> 1.
As E --> ∞, T --> 1, R --> 0.
(d) As E --> 0, nothing is transmitted past the first delta function.
As E --> ∞,everything is transmitted across both delta functions.
Problem:
Consider an electron trapped
in a one-dimensional periodic potential with period a.
The electron's potential
energy is given by
U(x) = ∑-∞+∞Aδ(x - na).
where A is a constant.
The eigenfunctions of the
Hamiltonian have the form Φ(x) =
exp(ikx)u(x), where u(x) is a periodic function with period a, u(x + a) = u(x)
(Bloch's theorem). Find the allowed energy eigenvalues of the electron.
Solution:
- Concepts:
Piecewise constant potentials
- Reasoning:
The potential energy is zero except at the location of the delta functions.
- Details of the calculation:
In the region from 0 to a, the
most general solution of the time-independent Schroedinger equation is Φ(x) =
B'exp(iαx)
+ B exp(-iαx), with α = (2mE/ħ2)½.
Because U(x) = U(x + a) we
also have Φ(x) = exp(ikx)u(x).
Therefore u(x) = B'exp(i(α - k)x)
+ B exp(-i(α + k)x).
At x = a,
Φ(x) is continuous,
but (∂/∂x)Φ(x)|a+ε
- (∂/∂x)Φ(x)|a-ε
= (2mA/ħ2) Φ(a).
When applying the boundary conditions at x = a use Φ(a) = exp(ikx)u(a) for the x = a +
ε side and the most general solution
for the x = a - ε side
of the boundary.
Φ(a + ε)ε-->0
= exp(ika)u(0) = exp(ika)(B' + B).
Φ(a - ε)ε-->0
= B'exp(iαa) + Bexp(-iαa).
Therefore
B'(exp(iαa)
- exp(ika)) = B(exp(ika) - exp(-iαa)).
As
ε-->0
we have
(∂/∂x)Φ(x)|a+ε
= (∂/∂x) exp(ikx)u(x)|a+ε
= ik exp(ika)u(0) + exp(ika)du/dx|0
= ik exp(ika)(B' + B) + exp(ika)(i(α-k)B' - i(α+k)B),
(∂/∂x)Φ(x)|a-ε
= iαB'exp(iαa)
- iαBexp(-iαa).
Therefore
ik exp(ika)(B' + B) + exp(ika)(i(α - k)B' - i(α + k)B) -
iαB'exp(iαa)
+ iαBexp(-iαa)
= (2mA/h2) Φ(a),
or
iαB'(exp(ika) - exp(iαa))
-iαB(exp(ika)
-
exp(-iαa) = (2mA/ħ2) Φ(a).
Insert from above and eliminate B.
2iαB'(exp(ika)
- exp(iαa)) = (2mA/ħ2)exp(ika)(B' + B)
= Cexp(ika)[B' + B' (exp(iαa)
- exp(ika))/(exp(ika) - exp(-iαa))].
Here C = 2mA/ħ2.
Recast the expression in terms of real functions.
2iαexp(ika)(exp(ika) - exp(-iαa))
- 2iαexp(iαa)(exp(ika) - exp(-iαa))
= Cexp(ika) [(exp(ika) - exp(-iαa) +
exp(iαa)
- exp(ika)].
2iα(exp(ika) - exp(-iαa))
- exp(iαa) + exp(-ika)) = iC sin(αa).
iα(cos(ka) - cos(αa))
= C [(exp(iαa) - exp(-iαa).
(C/(2α))sin(αa)
+ cos(αa) = cos(ka).
Let αa = x. Then (Ca/(2x))sinx
+ cosx = cos(ka).
All energies for which -1 < [(mAa/(ħ2x))sinx + cosx] < 1 are allowed.
Plot (Ca/(2x))sinx
+ cosx versus x. For example, let Ca/(2) = 5.
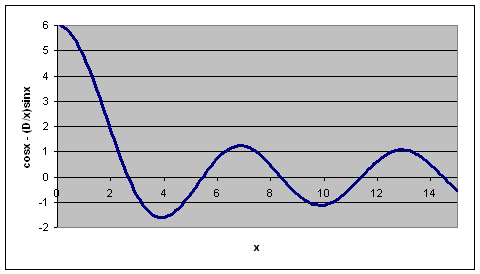
We have a set of forbidden and allowed bands.
Additional information:
Because U(x) = U(x + a) we
also have Φ(x) = exp(ikx)u(x).
Why?
Let Ta describe an operation called a translation. Every
part of the system is displaced by the amount a by this operation.
Let U(Ta) be the operator that maps the wave function before the
translation onto the wave function after the translation.
ψ'(x) = U(Ta)ψ(x)
= ψ(x - a).
For an infinitesimal translation (Δx
--> 0) ψ(x - Δx)
= ψ(x) - Δx(dψ(x)/dx)
= (1 - Δx(i/ħ)p)ψ(x)
Therefore U(TΔx)
= (1 - Δx(i/ħ)p).
(p denotes the momentum operator.)
U(Tx + Δx)
= U(Tx)U(TΔx)
= U(TΔx)U(Tx)
= (1 - Δx(i/ħ)p)U(Tx).
U(Tx + Δx)
- U(Tx) = -Δx(i/ħ)p)U(Tx).
dU(Tx)/dx = -(i/ħ)p)U(Tx),
U(Tx) = exp(-ikx),
with p = ħk.
Therefore U(Ta) = exp(-ika).
Note: U(Ta) is a unitary operator, it is not a Hermitian
operator.
It has complex eigenvalues of magnitude 1.
For a unitary operator there also exist a basis of orthonormal eigenfunctions.
The eigenfunctions of U(Ta) are of the form Φ(x) =
exp(ikx)u(x) with u(x + a) = u(x).
U(Ta)Φ(x) = Φ(x - a) =
exp(ikx)exp(-ika)u(x - a) =
exp(-ika)Φ(x)
.
The eigenvalue is exp(-ika).
For the given potential U(Ta) commutes with H, and
therefore U(Ta) and H have common eigenfunctions.
The eigenfunctions of H are therefore also of the form Φ(x) =
exp(ikx)u(x) with u(x + a) = u(x).




