Harmonic potentials, eigenvalues and eigenfunctions

Problem:

Find the average kinetic energy and the average potential energy of a particle in the ground state of a simple harmonic oscillator with frequency ω₀.

Solution:

• Concepts:
  Virial theorem 
• Reasoning:
  <T> = <U> for the harmonic oscillator.
• Details of the calculation:
  <E> = <T> + <U> = ½ħω₀ for the ground state.
  Therefore <T> = <U> = ¼ħω₀.

Problem:

Consider the one-dimensional problem in which a particle of mass m and charge -q is placed in a harmonic oscillator potential U(x) = ½mω²x² in the presence of an electric field E = E₀.
(a)  Write down the Hamiltonian H.
(b)  Find the eigenvalues of H.
(c)  Find <x> for all eigenstates of H.

Solution:

• Concepts:
  The eigenfunctions of the harmonic oscillator
• Reasoning:
  By changing the variable x to x' = x + qE₀/(mω²) we can make H look like the Hamiltonian of a simple harmonic oscillator.
• Details of the calculation:
  (a)  H = ½P²/m + ½mω²X² + qE₀X.
  (b)  H|Φ> = E|Φ>  ∂²Φ(x)/∂x² + (2m(E - ½mω²x² - qE₀x)/ħ²)Φ(x) = 0.
  Let us try to complete the square.
  ∂²Φ(x)/∂x² + (2m(E - ½mω²(x + qE₀/(mω²))² - q²E₀²/(2mω²))/ħ²)Φ(x) = 0.
  Let x' = x + qE₀/(mω²),  E' = E - q²E₀²/(2mω²).  Then
  ∂²Φ(x')/∂x^'2 + (2m(E' - ½mω²x'²)/ħ²)Φ(x') = 0.
  This is the equation for a harmonic oscillator in the absence of an electric field.
  E_n' = (n + ½)ħω,  E_n = (n + ½)ħω - q²E₀²/(2mω²).
  (c)  <x'> = 0  for all eigenstates,  <x> = -qE₀/(mω²) for all eigenstates.

Problem:

(a)   Give and sketch the probability distribution for the second lowest energy solution of the simple quantum mechanical harmonic oscillator,
-(ħ²/2m)(d²/dx²)Φ(x) + ½kx²Φ(x) = EΦ(x),
including the classical oscillator limits for the amplitude of oscillation.
(b)   Assume ψ(x,t = 0) = C₀Φ₀(x) + C₁Φ₁(x), and show that at later time
ψ(x,t) = C₀Φ₀(x)exp(-iE₀t/ħ) + C₁Φ₁(x)exp(-iE₁t/ħ).
(c)   Compute and sketch |ψ(x,t)|² for different times.

Solution:

• Concepts:
  The eigenstates of the harmonic oscillator, evolution operator
• Reasoning:
  We are asked to sketch an eigenfunction of the harmonic oscillator and to find ψ(x,t) given ψ(x,0)
• Details of the calculation:
  (a)  The three lowest eigenfunctions of the harmonic oscillator are (with k = mω²)
  Φ₀(x) = (mω/(πħ))^¼exp(-½mωx²/ħ),
  Φ₁(x) = ((4/π)(mω/ħ)³)^¼ x exp(-½mωx²/ħ),
  Φ₂(x) = (mω/(4πħ))^¼ [2mωx²/ħ - 1] exp(-½mωx²/ħ).
  The probability densities are given by |Φ_i(x)|².
  Below is a sketch of these functions with mω/h = 1.
  
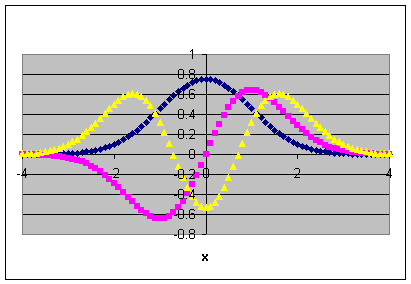
  The functions Φ₁(x), Φ₂(x) and Φ₃(x)
  
  
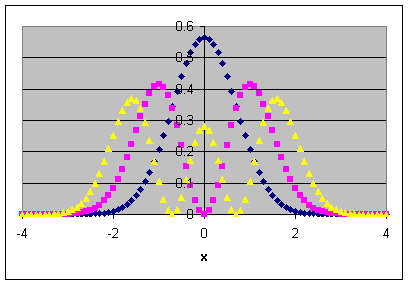
  The functions |Φ₁(x)|², |Φ₂(x)|² and |Φ₃(x)|²
  E_n = (n+½)ħω.
  For Φ_n(x) the classical oscillator limits for the amplitude of oscillation is found from
  ½kA² = (n + ½)ħω,  ½mω²A² = (n+½)ħω,  A² =  (2n + 1)ħ/(mω),  A = ((2n + 1)ħ/(mω))^½.
  (At the classical oscillator limits for the amplitude of oscillation the kinetic energy is zero and the potential energy equals the total energy.)
  (b)  |ψ(t)> = U(t,t₀)|ψ(t₀)>,  U(t,t₀) = exp(-(i/ħ)H(t-t₀)).
  ψ(x,t) = exp(-(i/ħ)H(t))[C₀Φ₀(x) + C₁Φ₁(x)] =
  C₀Φ₀(x)exp(-iE₀t/ħ) + C₁Φ₁(x)exp(-iE₁t/ħ).
  ψ(x,t) = exp(-mωx²/(2ħ))exp(-iωt)[C'₀ exp(iωt/2) + C₁'x exp(-iωt/2)].
  |ψ(x,t)|² = exp(-mωx²/ħ) [|C'₀|² + |C₁'|²x² + 2Re(C'₀C₁'x)cos(ωt)].
  Choose mω/ħ = 1, C'₁ = C'₂ = 1.
  Then |ψ(x,t)|² = exp(-x²) [1 + x² + 2xcos(ωt)].
  
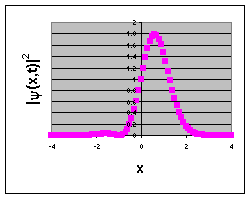
  ωt = 0
  
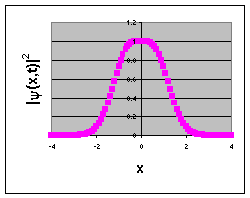
  ωt = π/2
  
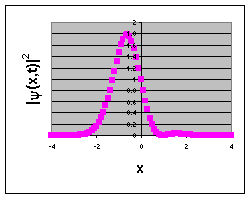
  ωt = π
  <x>(t) oscillates with frequency ω like the classical coordinate x.

Problem:

A non-relativistic quantum mechanical particle of mass m is in a 1-dimensional potential,
U(x) = ax² for x > 0 and U(x) = ∞ for x < 0.

(a)  Find the possible energy eigenvalues and normalized eigenfunctions.
(b)  The particle is in the ground state.  At what position x is it most likely to be found?
(c)  What is the expectation value of the particle position?

Solution:

• Concepts:
  The harmonic oscillator
• Reasoning:
  For x > 0, the given potential is identical to the harmonic oscillator potential.
  Odd harmonic oscillator energy eigenfunctions are zero at x = 0 and, satisfy all boundary conditions for x > 0.  They are eigenfuctions of H for the given potential for x > 0.  For x < 0, the eigenfunctions of the given H are zero.
• Details of the calculation:
  (a)  The harmonic oscillator eigenfunctions with V(x) = ½mω²x² are
  Φ_n(x) = (n! 2ⁿ)^-½ (β/√π)^½H_n(η) exp(-½η²),  where η = (mω/ħ)^½ x = βx.

  If we replace ω by (2a/m)^½ and multiply  the functions with n = odd by √2, we obtain the normalized eigenfunctions for the given H.  The eigenvalues are
  E_n = (n + ½ )ħω = (n + ½ )ħ(2a/m)^½, n = odd.
  (b)  The ground state wave function is Φ₁(x) = N₁ x exp(-(2ma)^½x²/(2ħ)), x > 0,
  with N₁ = (2/π^¼)((2ma)^½/ħ)^¾
  The most probable position is found from d|Φ₁(x)|²/dx = 0.
  x - (2ma)^½x³/ħ = 0, x = ħ^½/ (2ma)^¼.
  (c)  The the expectation value of x is
  <x> = ∫₀^∞ x |Φ₁( x )|²d x = N₁²(ħ²/(2ma))∫₀^∞ y³ exp(-y ²) dy
  = (4/√π)[(2ma)^¾/ħ^3/2](½ħ²/(2ma)) = 1.13√ħ/(2ma)^¼.
  <x> = 1.13 ħ^½/(2ma)^¼.

Problem:

Write down the energy eigenvalues for the one-dimensional Schroedinger equation with
U(x) = ½ m ω²x² for x > 0 and U(x) = ∞ for x < 0.

Solution:

• Concepts:
  The eigenfunctions of the 1D harmonic oscillator
• Reasoning:
  The odd eigenfunctions of the harmonic oscillator with U(x) = ½ m ω²x² for all x are eigenfunctions of H for this potential.
• Details of the calculation:
  The eigenvalues therefore are E = (n + ½)ħω, n = odd
  or rewriting, E = (2n + 3/2)ħω, n = 0, 1, 2, ...