Infinite wells
Problem:
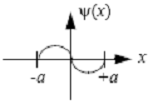
The figure below shows one of the possible
energy eigenfunctions ψ(x) for a particle bouncing freely back and forth between
impenetrable walls located at x = -a and x = +a. The potential energy equals
zero for |x| < a. If the energy of the particle is 2 eV when it is in the
quantum state associated with this eigenfunction, find the energy when it is in
quantum state of lowest possible energy.
Solution:
- Concepts:
The infinite square well
- Reasoning:
We are asked to identify which eigenfunction of the infinite square well is
shown in the figure.
- Details of the calculation:
The eigenfunctions of H are ψn(x) = (1/a)½sin(nπ(x+a)/(2a))
with eigenvalues
En = n2π2ħ2/(8ma2).
ψ2(x) is shown in the figure.
E2 = 2 eV, E1 = ½ eV is the lowest possible energy
eigenvalue.
Problem:
A particle in a 1-D box has a minimum allowed energy of 2.5 eV.
(a) What is the next higher energy it can have? And the next higher after
that? Does it have a maximum allowed energy?
(b) If the particle is an electron, how wide is the box?
(c) The fact that particles in a 1-D box have a minimum energy is not completely
unrelated to the uncertainty principle. Using the minimum energy, find
the minimum magnitude of the momentum of a particle, with mass m, trapped in a
1-D box of size L in classical mechanics. How does this compare with the
momentum uncertainty required by the uncertainty principle, if we assume Δx = L?
Solution:
- Concepts:
The 1-D infinite square well, the uncertainty principle.
- Reasoning:
We are asked to find the energy levels of a particle in a one-dimensional
infinite square well.
- Details of the calculation:
(a) En = n2π2ħ2/(2mL2)
E1 = 2.5 eV, E2 = 4*2.5 eV = 10 eV, E3 =
9*2.5 eV = 22.5 eV. There is no upper limit
(b) 2.5 eV*1.6*10-19J/eV = π2(1.05*10-34
Js)2/(2*9.109*10-31 kg * L2)
L = 3.86*10-10 m.
The box has a width that is comparable to the typical size of an atom.
(c) E1 = pmin2/(2m), pmin2
= (2*9.109*10-31 kg*2.5 eV*1.6*10-19J/eV),
pmin = 8.5*10-25.
Δp = ħ/Δx =
(1.05*10-34 Js)/(3.86*10-10 m) = 2.7*10-25
kgm/s. The minimum momentum required by the uncertainty principle is p =
Δp.
Δp and pmin have the same order of
magnitude.
Problem:
An electron (m = 9.11*10-31 kg) moves
with a speed v = 3.8*106 m/s (non-relativistic) back and forth inside
a one-dimensional box (U = 0) of length L. The potential is infinite elsewhere,
hence the electron may not escape the box.
(a) If the electron were a classical particle, what would
be its energy?
(b) Now treat the electron quantum-mechanically but assume
it has the energy you found in part (a). If the quantum number associated with
the state of the electron is n = 2, what is the length of the box?
(c) What is the energy of the ground state?
(d) Write down the wave function for the first excited state.
Solution:
- Concepts:
The infinite square well
- Reasoning:
The electron moves in an infinite square well potential in one dimension.
- Details of the calculation:
(a) We are told that we can approach the problem non-relativistically.
K = ½mv2 = 0.5*(9.11*10-31 kg)*(3.8*106
m/s) = 6.577*10-18 J = 41.1 eV.
(b) The
energy for a particle in a box is given by
En =
ħ2n2π2/(2mL2).
Solving the above equation for L gives L = (ħ2n2π2/(2mE))½
= 0.191 nm.
(c) E1 = En/n2 = 41.1 eV/4 =
10.3 eV.
(d) The general expression for the wave function for a
particle in a box is given by
ψn(x) = (2/L)½sin(nπx/L).
With n = 2 this expression becomes ψ2(x) = (2/L)½sin(2πx/L).
We can substitute in the value for L that we found in part (b).
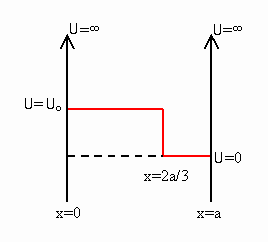
Problem:
For the infinite well shown, the wave function for a particle of mass m,
at t = 0, is
ψ(x, t = 0) = (2/a)½sin(3πx/a).
(a) Is ψ(x, t = 0) an eigenfunction
of the Hamiltonian?
(b) Calculate <X>, <Px>, and <H> at t = 0. U
Solution:
- Concepts:
The eigenfunctions of the infinite square well, the postulates of quantum
mechanics.
- Reasoning:
We recognize that the given wave function is an eigenfunction of the
infinite square well. The mean value of any observable A is <ψ|A|ψ>.
- Details of the calculation:
(a)
ψ(x, t = 0) = (2/a)½sin(3πx/a) is not an eigenfunction of the Hamiltonian.
(b)
<x> = (2/a)∫0adx
x sin2(3πx/a)
= a/2.
<px> = (2/a)∫0adx
sin(3πx/a) (ħ/i) ∂sin(3πx/a)/∂x
= C ∫0adx
sin(3πx/a) cos(3πx/a)
= 0.
<H> = <T> + <U>. ψ is an eigenfunction of the infinite
square well with U = 0 for 0 < x < a.
For the infinite square
well we have <H> = E = <T>.
Therefore <T> = n2π2ħ2/(2ma2)
=
9π2ħ2/(2ma2).
<U> =
∫0a ψUψ dx
=
∫02a/3
ψU0ψ dx
= (2/a)∫02a/3dx
U0 sin2(3πx/a)
= 2U0/3.
<H> = 9π2ħ2/(2ma2)
+ 2U0/3.
Problem:
A particle of mass m moves in one dimension in a square well with walls of
infinite height a distance L apart. The particle is known to be in a state
consisting of an equal admixture of the two lowest energy eigenstates of the
system. Find the probability as a function of time that the particle will be
found in the right-hand half of the well.
Solution:
- Concepts:
The postulates of quantum mechanics
- Reasoning:
When a physical quantity described by the operator A is measured on
a system in a normalized state |ψ>,
the probability of measuring the eigenvalue aα
is given by dP(aα)
= |<uα|ψ>|2dα, where |uα>
is the eigenvector corresponding to the eigenvalue aα;
we assume aα is a non-degenerate
continuous eigenvalue of A.
Therefore dP(x,t) = |<x|ψ>|2dx = |ψ(x,t)|2dx.
- Details of the calculation:
ψ(x,t) = 2-½[ψ1(x,t) + ψ2(x,t)],
where
ψ1(x,t) = (2/L)½sin(πx/L)exp(-(2πi/h)E1t),
ψ2(x,t) = (2/L)½sin(2πx/L)exp(-(2πi/h)E2t),
with
E1 = h2/(8mL2), E2 = h2/(2mL2)
are solutions to the one-dimensional infinite square-well problem.
P(x,t) = |ψ(x,t)|2 is the
probability per unit length of finding the particle at position x.
P(x,t) = (1/L)[sin2(πx/L) + sin2(2πx/L) + 2sin(πx/L)sin(2πx/L)cos(2π(E2-E1)t/h)].
∫L/2LP(x,t)dx
= (1/L)[(L/4) + (L/4) + (4L/3π)cos(2π(E2-E1)t/h)]
= ½ + (4/3π)cos(3h2t/(8mL2)).
Problem:
Consider a particle of mass m in an one-dimension infinite square well of
length L. Assume that the particle is in the nth eigenstate (n = 1, 2, 3, ... ).
(a) The momentum is measured. Show that the probability distribution Pn(k)
for measuring a momentum p = ħk is Pn(k) = [2πLn2/(k2L2
- n2π2)2] [1 + (-1)n+1cos(kL)].
(b) What outcome of a momentum measurement is most likely? Does your result
agree with your intuition?
(c) Which momenta cannot be the result of a momentum measurement? Why is that
so?
Solution:
- Concepts:
The square well potential, postulates of QM, the Fourier transform
- Reasoning:
Let U(x) = 0, 0 < x < L, U(x) = infinite everywhere else.
The normalized stationary states <x|ψ > = ψ(x) in this potential are
ψn(x) = (2/L)½sin(nπx/L) = (2/L)½sin(knL),
kn = nπ/L, in coordinate representation.
To change from the {|x>} basis to the {|p>} basis we use
<p|ψ > = ∫dx<p|x><x|ψ > = (2πħ)-½ ∫dx exp(-ipx/ħ)
ψ(x) = ψ(p).
|ψ(p)|2 is the probability density distribution Pn(p). Pn(p)dp
= Pn(k)dk, Pn(k) = ħ Pn(p).
- Details of the calculation:
(a)
ψn(p) = (πħL)-½ ∫0Ldx exp(-ipx/ħ)
sin(nπx/L)
∫0Ldx exp(-ipx/ħ) sin(nπx/L) = ∫0Ldx
exp(-ikx) sin(knx)
= ∫0Ldx cos(kx)sin(knx) - i∫0Ldx
sin(kx)sin(knx)
= (cos((k-kn)L) - 1)/(2(k-kn)) - (cos((k+kn)L)
- 1)/(2(k+kn))
-i[sin((k-kn)L)/(2(k-kn)) - sin((k+kn)L)/(2(k+kn))
= (-1)nexp(ikL)/(2(k-kn)) - (-1)nexp(ikL)/(2(k+kn))
- 1/(2(k-kn)) + 1/(2(k+kn))
= [(-1)nexp(ikL) - 1]kn/(k2 - kn2)
= [(-1)nexp(ipL/ħ) - 1](nπħ2L)/(p2L2
- n2π2ħ2).
ψn(p) = [nħ3/2(πL)½/(p2L2
- n2π2ħ2)] [(-1)nexp(ipL/ħ) - 1].
Pn(p) = |ψn(p)|2 = [2πLn2ħ3/(p2L2
- n2π2ħ2)2] [1 + (-1)n+1cos(pL/ħ)].
Pn(k) = ħ Pn(p) = [2πLn2/(k2L2
- n2π2)2] [1 + (-1)n+1cos(kL)].(b)
If the particle is in the nth eigenstate then the probability of measuring a
momentum p is
Pn(p) = (2πLn2/ħ)[1 + (-1)n+1cos(pL/ħ)]/(p2L2/ħ2
- n2π2)2
= (2πLn2/ħ)[ [1 + (-1)n+1cos(pL/ħ)]/(pL/ħ + nπ)2(pL/ħ
- nπ)2.
(Note n is a given integer.)
If pL = ±n'πħ, then (-1)n'+1cos(pL/ħ) = (-1)n'+1cos(±n'π)
= (-1)n'+1(-1)n' = -1, for any n'.
If n' = n, both the numerator and the denominator of Pn(p) are
zero.
If we expand the cosine function about these points we have
1 + (-1)n+1cos(pL/ħ)] = 1 + (-1)n+1(-1)n(1
- (pL/ħ - nπ)2/2) + (pL/ħ - nπ)4/4 ... )
= (pL/ħ - nπ)2/2 - (pL/ħ - nπ)4/4
and
Pn(p) = (πLn2/ħ)/(pL + nπħ)2 (1 - (pL/ħ - nπ)2/2).
Pn(p) --> L/(4πħ)( 1 - (pL/ħ - nπ)2/2) as pL
--> ±nπħ.
The maxima of Pn(p) are at p = ±nπħ/L.
The most likely outcome of a momentum measurement is ħk = ±nπħ/L.
(c) We need [1 + (-1)n'+1cos(pL/ħ)] = 0, pL = ±n'πħ,
and n' ≠ n.
Momenta p = ±n'πħ/L, n' ≠ n cannot be the result of a momentum measurement.


